Что такое дроби 5 класс математика

Статья рассказывает о дробях в математике для учеников 5 класса. Она объясняет основные понятия, правила работы с дробями и показывает, как решать задачи с использованием дробей. На сайте вы найдете примеры, упражнения и интерактивные задания для углубленного изучения этой темы.

В математике дроби – это одна из важнейших тем, которую изучают в 5 классе. Дробь – это числовая дробь, которая состоит из двух частей: числителя и знаменателя, разделенных чертой. Числитель – это число, которое находится над чертой, а знаменатель – число, находящееся под чертой. Дроби используются для представления долей от целого числа или для деления одного числа на другое.

Важно понимать, что дроби могут быть эквивалентными, то есть иметь одно и то же числовое значение, но разные записи. Например, дроби 1/2 и 2/4 равны друг другу. Для упрощения дробей существуют правила, которые позволяют привести их к наименьшему общему знаменателю и сократить до простейшего вида.

Для сложения и вычитания дробей необходимо иметь дроби с одинаковыми знаменателями. Если знаменатели разные, то нужно привести дроби к общему знаменателю. Затем числители складываются или вычитаются, а знаменатель остается неизменным.

В 5 классе математики ученики также изучают умножение и деление дробей. При умножении дробей числители и знаменатели перемножаются отдельно. Для деления дробей нужно помножить первую дробь на обратную второй дроби. Также важно уметь решать задачи с дробями, которые могут включать в себя активности, фрагменты геометрических фигур и другие реальные ситуации.

Основное понятие о дробях

Числитель показывает, сколько частей целого числа мы имеем или берем, а знаменатель показывает, на сколько равных частей разделено целое число. Например, в дроби 3/4, мы берем 3 части из 4 равных частей, на которые разделено целое число.

Дроби могут быть обыкновенными и десятичными. Обыкновенные дроби представляются в виде числителя и знаменателя, а десятичные дроби представляются в виде десятичной дроби с запятой.

Например, дробь 2/3 означает, что мы берем 2 части из 3 равных частей целого числа. Десятичная дробь 0,75 означает, что мы имеем 75 сотых части от целого числа.

Дроби используются в математике для представления долей, долей чисел и вещественных чисел, а также в решении различных задач и вычислениях.

Видео по теме:

Числитель и знаменатель дроби

Числитель обозначается верхней цифрой в дроби, а знаменатель — нижней. Например, в дроби 3/5 числитель равен 3, а знаменатель равен 5.

Числитель и знаменатель имеют разное значение:

Числитель:

• Определяет количество частей, которые нужно взять из целого числа.
• Может быть любым натуральным числом (целым положительным числом) или нулем.
• Числитель всегда указывается перед знаменателем.

Знаменатель:

• Определяет количество частей, на которые разделено целое число.
• Должен быть натуральным числом (целым положительным числом) и не может быть равным нулю.
• Знаменатель всегда указывается после числителя, разделенного чертой.

Знание о числителе и знаменателе позволяет понять, какую часть от целого представляет собой дробь и какие операции можно выполнять с дробями.

Например, дробь 3/5 означает, что из целого числа нужно взять 3 части, разделенные на 5 равных частей.

Числитель и знаменатель являются важными понятиями в теме дробей и используются при выполнении операций сложения, вычитания, умножения и деления с дробями.

Формы записи дробей

Дроби представляют собой числа, которые записываются в виде дробной части, числителя и знаменателя. Существует несколько форм записи дробей, которые мы рассмотрим.

Десятичная дробь — это дробь, в которой числитель представлен десятичной дробью. Например, дробь 0,5 является десятичной дробью.

Обыкновенная дробь — это дробь, в которой числитель и знаменатель представлены обыкновенными числами. Например, дробь 1/2 является обыкновенной дробью.

Смешанная дробь — это дробь, которая состоит из целой части и обыкновенной дроби. Например, дробь 1 1/2 является смешанной дробью.

Все эти формы записи дробей имеют свои особенности и применяются в разных ситуациях. При решении задач на дроби необходимо уметь переводить дроби из одной формы записи в другую.

Вопрос-ответ:

Какое определение дроби в 5 классе?

Дробью в математике называется отношение двух чисел, записываемое в виде a/b, где числитель a — это количество равных частей, а знаменатель b — это количество таких частей, на которые разделено целое число.

Какие основные правила работы с дробями в 5 классе?

Основные правила работы с дробями в 5 классе включают сложение, вычитание, умножение и деление дробей, а также сравнение дробей на больше, меньше или равно. Правила включают в себя нахождение общего знаменателя, сокращение дробей, умножение и деление дробей на целое число и нахождение десятичной записи дроби.

Какие задачи можно решить с использованием дробей в 5 классе?

С использованием дробей в 5 классе можно решать задачи на разделение предметов на равные части, на сложение и вычитание долей, а также на сравнение долей. Например, задачи на разделение пиццы на равные кусочки или на сложение половинок яблок.

Как можно упростить или сократить дробь?

Для упрощения или сокращения дроби нужно найти общий делитель числителя и знаменателя и разделить оба числа на этот общий делитель. Например, если числитель и знаменатель дроби делятся на 2, то можно дробь сократить, поделив числитель и знаменатель на 2.

Основные правила работы с дробями

Дроби представляют собой числа, состоящие из двух частей: числителя и знаменателя, разделенных чертой. Числитель указывает, сколько частей целого имеется, а знаменатель показывает, на сколько частей целое разделено.

При работе с дробями соблюдаются следующие основные правила:

1. Сложение и вычитание дробей. Для сложения или вычитания дробей их знаменатели должны быть одинаковыми. Если знаменатели разные, их нужно привести к общему знаменателю. Для этого знаменатели дробей приводят к наименьшему общему кратному и затем дроби складывают или вычитают, не изменяя числители.
2. Умножение дроби на целое число. Для умножения дроби на целое число достаточно умножить числитель дроби на это число, а знаменатель оставить без изменений.
3. Умножение дроби на дробь. Для умножения двух дробей их числители и знаменатели умножаются друг на друга.
4. Деление дробей. Деление одной дроби на другую эквивалентно умножению первой дроби на обратную второй дробь. Обратная дробь получается путем перестановки числителя и знаменателя.
5. Сокращение дроби. Чтобы сократить дробь, нужно числитель и знаменатель дроби поделить на их общий делитель.

Правильное применение этих правил позволяет выполнять арифметические операции с дробями и решать задачи, связанные с их использованием.

Правило сравнения дробей

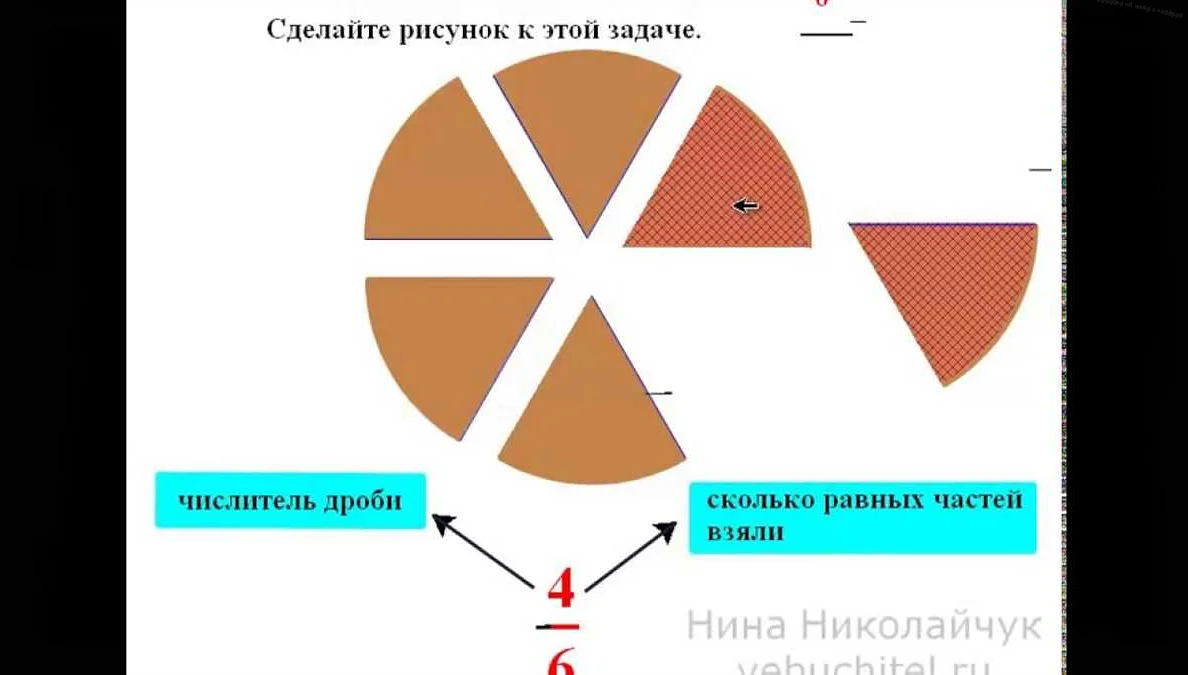
Правило сравнения дробей позволяет установить, какая из двух дробей больше, меньше или равна другой дроби.

Для сравнения дробей необходимо выполнить следующие шаги:

1. Привести дроби к общему знаменателю.
2. Сравнить числители дробей.
3. Если числитель первой дроби больше числителя второй дроби, то первая дробь больше второй. Если числитель первой дроби меньше числителя второй дроби, то первая дробь меньше второй. Если числители равны, переходим к следующему шагу.
4. Сравнить знаменатели дробей.
5. Если знаменатель первой дроби больше знаменателя второй дроби, то первая дробь меньше второй. Если знаменатель первой дроби меньше знаменателя второй дроби, то первая дробь больше второй. Если знаменатели равны, значит, дроби равны.

Правило сравнения дробей является одним из основных понятий при работе с дробями и позволяет установить отношение между ними.

Операции с дробями

В математике существует несколько основных операций с дробями: сложение, вычитание, умножение и деление. Давайте рассмотрим каждую из них подробнее.

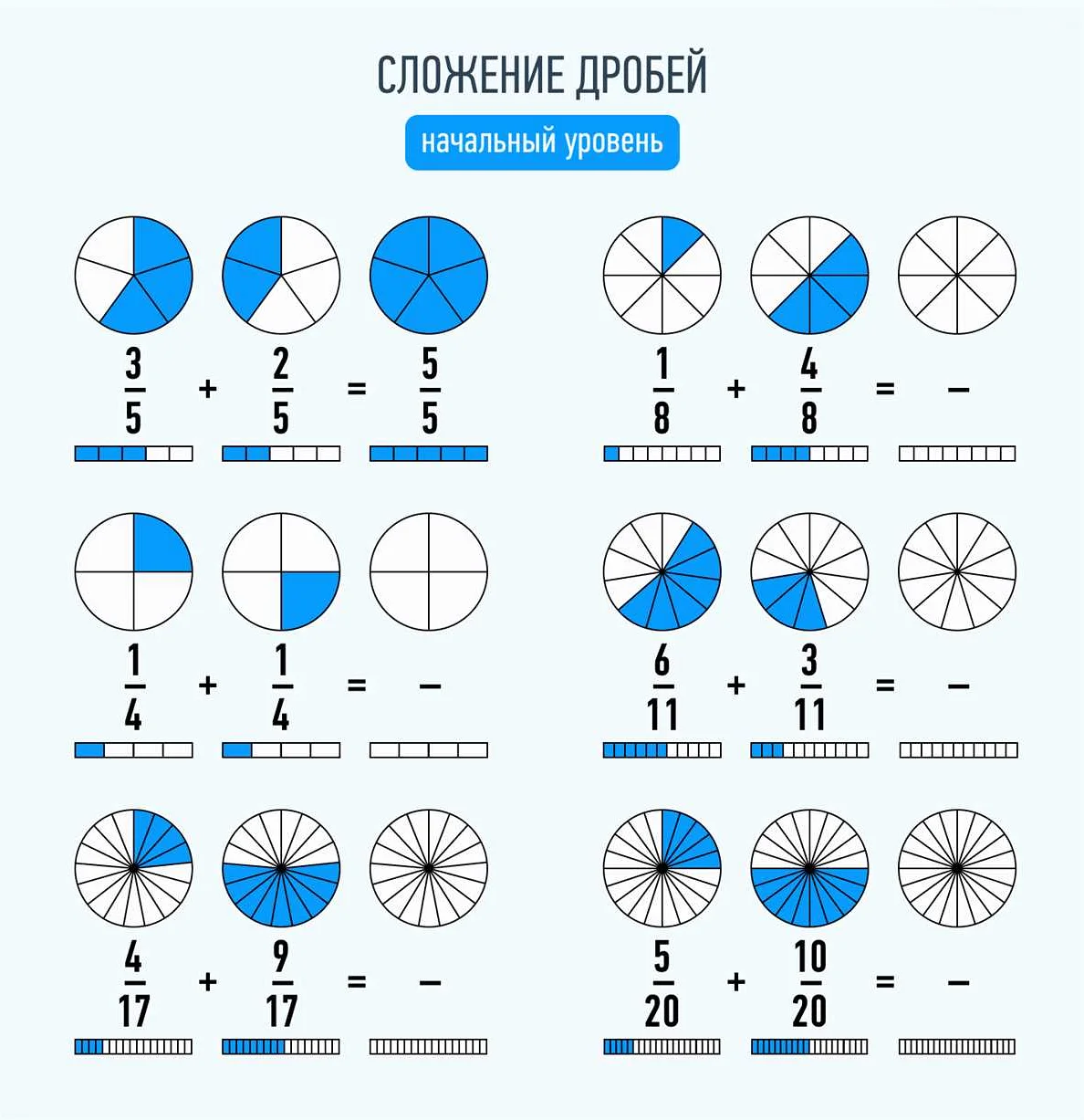
Сложение дробей выполняется следующим образом: если знаменатели дробей одинаковы, то сложение числителей даст нам числитель суммы. Например:

1/4 + 2/4 = (1 + 2)/4 = 3/4

Если знаменатели разные, необходимо привести дроби к общему знаменателю, а затем сложить числители. Например:

1/3 + 1/2 = (1 * 2)/(3 * 2) + (1 * 3)/(2 * 3) = 2/6 + 3/6 = (2 + 3)/6 = 5/6

Вычитание дробей выполняется аналогичным образом. Если знаменатели дробей одинаковы, то разность числителей даст нам числитель разности. Например:

3/5 — 1/5 = (3 — 1)/5 = 2/5

Если знаменатели разные, необходимо привести дроби к общему знаменателю, а затем вычесть числители. Например:

2/3 — 1/4 = (2 * 4)/(3 * 4) — (1 * 3)/(4 * 3) = 8/12 — 3/12 = (8 — 3)/12 = 5/12

Умножение дробей выполняется умножением числителей и знаменателей дробей. Например:

3/4 * 2/5 = (3 * 2)/(4 * 5) = 6/20 = 3/10

Деление дробей выполняется умножением первой дроби на обратную второй дробь. Например:

3/4 ÷ 2/5 = (3/4) * (5/2) = (3 * 5)/(4 * 2) = 15/8

Помните, что при выполнении операций с дробями необходимо упрощать полученные результаты, если это возможно. Также не забывайте проверять правильность выполненных операций путем приведения дробей к наименьшему общему знаменателю и сравнения числителей.

Задачи на сложение и вычитание дробей

При решении задач на сложение и вычитание дробей необходимо использовать основные правила работы с дробями. Они включают в себя следующие шаги:

1. Найти общий знаменатель для дробей, которые нужно сложить или вычесть.
2. Привести каждую дробь к общему знаменателю, умножив числитель и знаменатель на одно и то же число.
3. Сложить или вычесть числители дробей.
4. Если возможно, упростить полученную дробь.

Рассмотрим примеры задач на сложение и вычитание дробей:

Пример 1: Сложить дроби 1/3 и 2/5.

Решение:

1. Общий знаменатель для дробей 1/3 и 2/5 равен 15.
2. Приведем каждую дробь к общему знаменателю: 1/3 = 5/15 и 2/5 = 6/15.
3. Сложим числители дробей: 5/15 + 6/15 = 11/15.
4. Упростим полученную дробь, если возможно.

Пример 2: Вычесть дробь 2/3 из дроби 3/4.

Решение:

1. Общий знаменатель для дробей 3/4 и 2/3 равен 12.
2. Приведем каждую дробь к общему знаменателю: 3/4 = 9/12 и 2/3 = 8/12.
3. Вычтем числители дробей: 9/12 — 8/12 = 1/12.
4. Упростим полученную дробь, если возможно.

Таким образом, при решении задач на сложение и вычитание дробей необходимо правильно находить общий знаменатель и проводить соответствующие операции с числителями дробей. Важно помнить о необходимости упрощения полученных дробей, если это возможно.

Задачи на умножение и деление дробей

Примеры задач на умножение дробей:

ЗадачаРешение

Найдите произведение дробей: $\frac{2}{3} \cdot \frac{5}{6}$	Для умножения дробей нужно умножить числитель на числитель и знаменатель на знаменатель. Получим: $\frac{2 \cdot 5}{3 \cdot 6} = \frac{10}{18}$. Затем сокращаем дробь: $\frac{10}{18} = \frac{5}{9}$.
Найдите произведение дробей: $\frac{3}{4} \cdot \frac{2}{5}$	Проводим аналогичные действия: $\frac{3 \cdot 2}{4 \cdot 5} = \frac{6}{20}$. Сокращаем: $\frac{6}{20} = \frac{3}{10}$.

Примеры задач на деление дробей:

ЗадачаРешение

Разделите дроби: $\frac{4}{5} \div \frac{2}{3}$	Для деления дробей нужно умножить первую дробь на обратную второй. Получим: $\frac{4}{5} \cdot \frac{3}{2} = \frac{12}{10}$. Сокращаем: $\frac{12}{10} = \frac{6}{5}$.
Разделите дроби: $\frac{7}{8} \div \frac{4}{9}$	Выполняем аналогичные действия: $\frac{7}{8} \cdot \frac{9}{4} = \frac{63}{32}$. Дробь уже несократимая.

Важно помнить, что перед умножением и делением дробей необходимо привести их к общему знаменателю. Также следует уметь сокращать полученные дроби.

Решение задач на умножение и деление дробей требует понимания основных правил и навыков работы с дробями. Чем больше практики, тем легче станет решать подобные задачи.