Что такое подмножество дробей в математике 6 класс

Подмножество дробей в математике 6 класса — это набор дробей, состоящий из частей числителя и знаменателя, где числитель и знаменатель являются целыми числами или натуральными числами, и каждая дробь может быть представлена в виде отношения числа к числу или целого числа к натуральному числу.

В математике 6 класса особое внимание уделяется изучению дробей — чисел, которые представляются в виде отношения двух целых чисел. Подмножество дробей является важной темой, которую необходимо освоить для успешного продолжения обучения.

Одним из основных понятий, связанных с подмножеством дробей, является простая дробь. Простая дробь представляет собой дробь, у которой числитель меньше знаменателя. Например, дроби 1/2, 3/4 и 5/6 являются простыми дробями. Они часто встречаются в повседневной жизни и имеют простое понимание.

Другим важным понятием в подмножестве дробей является смешанная дробь. Смешанная дробь представляет собой сумму целого числа и простой дроби. Например, 2 1/3 и 3 3/4 — это смешанные дроби. Они имеют специальное представление и требуют понимания правил их преобразования.

Понимание подмножества дробей является фундаментальным для дальнейшего изучения математики. Оно позволяет решать разнообразные задачи и применять полученные знания на практике.

Что такое подмножество дробей?

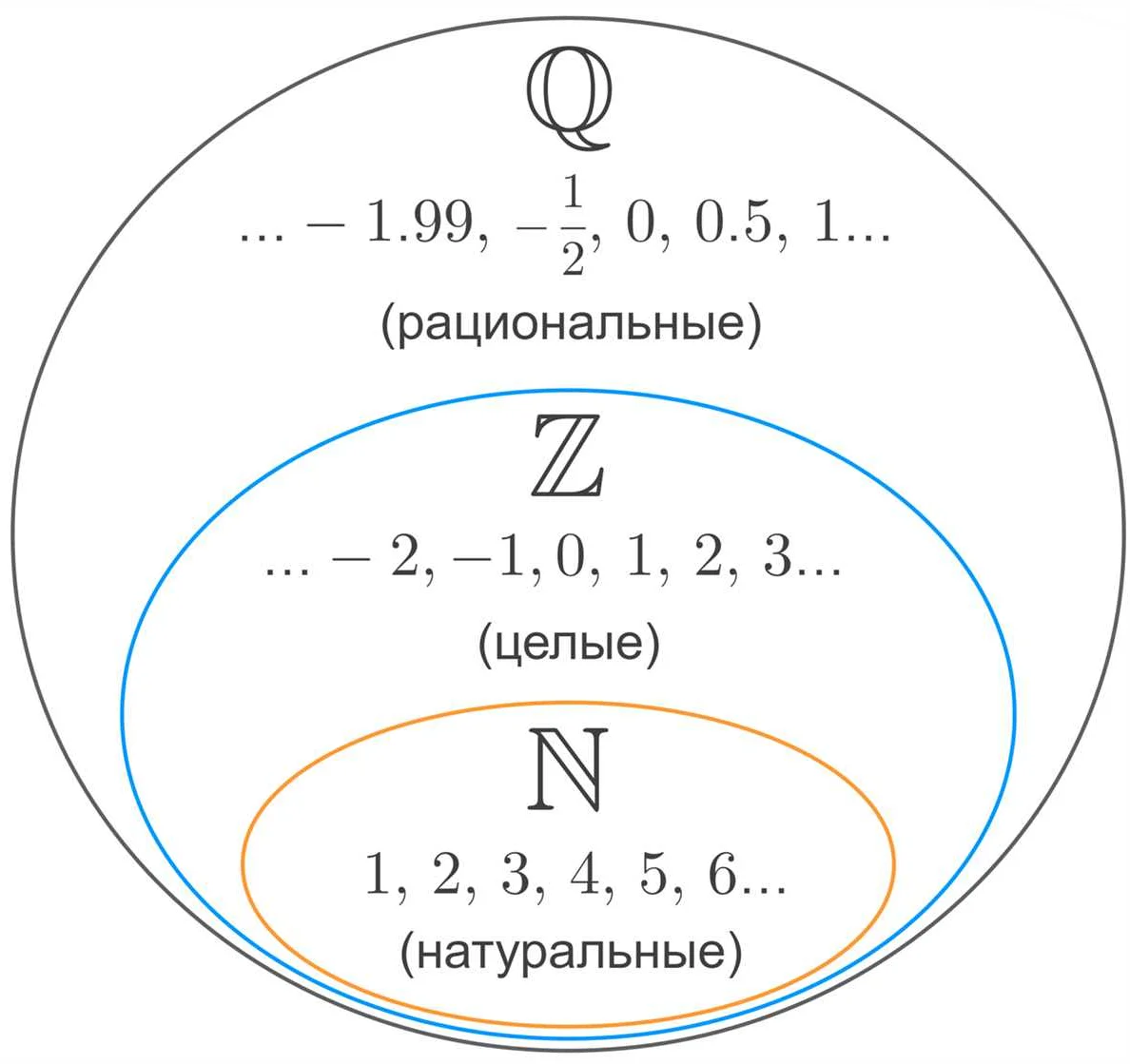
Например, подмножество дробей может состоять из всех дробей, у которых знаменатель равен 5. В этом случае, все дроби с знаменателем 5 будут входить в данное подмножество. Примерами таких дробей могут быть 1/5, 2/5, 3/5 и т.д.

Также подмножество дробей может быть определено на основе общего числителя. Например, подмножество дробей может состоять из всех дробей, у которых числитель равен 3. В этом случае, все дроби с числителем 3 будут входить в данное подмножество. Примерами таких дробей могут быть 3/4, 3/7, 3/9 и т.д.

Подмножество дробей позволяет классифицировать и группировать дроби в математике, чтобы упростить их анализ и решение различных задач. Оно помогает выделить дроби с общими свойствами и использовать их для более эффективной работы с дробями.

Основные понятия

В числителе и знаменателе дроби могут стоять как целые числа, так и десятичные. Дроби могут быть записаны в виде обыкновенной или десятичной.

Обыкновенная дробь состоит из числителя и знаменателя, которые отделяются знаком «/». Например, 3/4.

Десятичная дробь представляет собой число, в котором после запятой стоит бесконечное количество знаков. Например, 0.25.

Дроби могут быть сокращаемыми и несократимыми. Сократимая дробь — это дробь, в которой числитель и знаменатель имеют общие множители и могут быть упрощены. Несократимая дробь — это дробь, в которой числитель и знаменатель не имеют общих множителей и не могут быть упрощены.

В таблице ниже представлены основные понятия, связанные с дробями:

ТерминОписание

Числитель	Число, которое делим
Знаменатель	Число, на которое делим
Обыкновенная дробь	Дробь вида «числитель/знаменатель»
Десятичная дробь	Дробь, представленная в виде числа с бесконечным количеством знаков после запятой
Сократимая дробь	Дробь, которую можно упростить путем сокращения числителя и знаменателя
Несократимая дробь	Дробь, которую нельзя упростить путем сокращения числителя и знаменателя

Простые дроби

Простые дроби можно записывать в виде обыкновенных десятичных дробей, представляя числитель в виде целого числа, а знаменатель в виде степени десятки. Например, 1/3 можно записать как 0.333, а 2/5 как 0.4.

Простые дроби часто используются для представления частей целых чисел. Например, если у нас есть пирог, разделенный на 8 равных частей, то каждая часть будет соответствовать простой дроби 1/8. Если мы возьмем две таких части, то получим простую дробь 2/8, которую можно сократить до 1/4.

Важно понимать, что простые дроби всегда представляют часть от целого числа и могут быть записаны как десятичные дроби.

Примеры:

• Простая дробь 1/2 представляет половину целого числа.
• Простая дробь 3/4 представляет три четверти целого числа.
• Простая дробь 2/3 представляет две трети целого числа.

Важно: При работе с простыми дробями необходимо уметь сокращать дроби до наименьшего знаменателя и приводить их к наиболее простому виду.

Смешанные числа

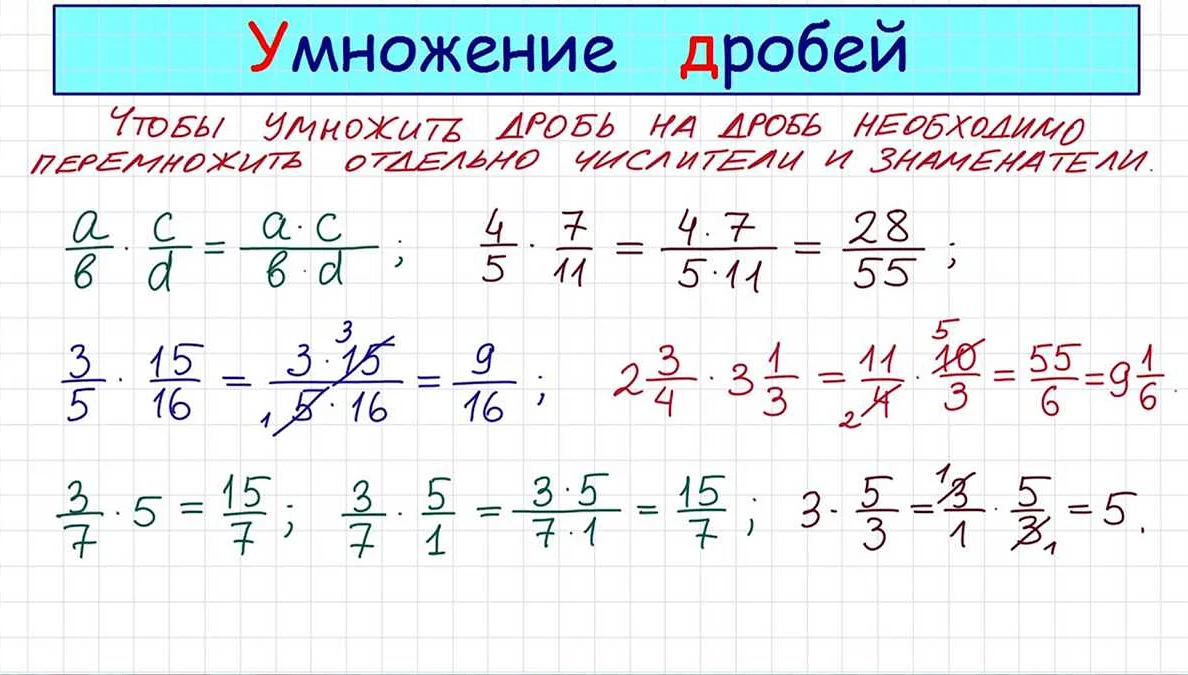
В математике смешанные числа представляют собой комбинацию целой части и десятичной дроби. Они используются для записи нецелых чисел в более удобной форме.

Смешанное число записывается в виде целой части, обозначенной целым числом, и дроби, обозначенной десятичной дробью. Например, число 3 ½ представляет собой смешанное число, где 3 — целая часть, а ½ — дробная часть.

Смешанные числа можно использовать при сложении, вычитании, умножении и делении. Для выполнения операций со смешанными числами необходимо преобразовать их в обыкновенные дроби. Например, для сложения двух смешанных чисел необходимо сложить их целые части и дробные части отдельно.

Смешанное числоЦелая частьДробная часть

3 ½	3	½
4 ¼	4	¼
2 ¾	2	¾

Смешанные числа могут быть представлены в виде обыкновенных дробей. Например, смешанное число 3 ½ равно обыкновенной дроби 7/2. Для этого необходимо умножить целую часть на знаменатель и прибавить числитель дробной части. В данном случае, 3 * 2 + 1 = 7.

Использование смешанных чисел упрощает запись нецелых чисел и позволяет выполнять операции с ними более легко и наглядно.

Примеры

1. Разложим дробь 1/2 на сумму двух дробей с общим знаменателем:

• 1/2 = 1/4 + 1/4

2. Сложим дроби 1/3 и 1/6:

• 1/3 + 1/6 = 2/6 + 1/6 = 3/6
• Упростим полученную дробь:
• 3/6 = 1/2

3. Вычтем из дроби 3/4 дробь 1/8:

• 3/4 — 1/8 = 6/8 — 1/8 = 5/8

4. Умножим дробь 2/5 на 3:

• 2/5 * 3 = 6/5

5. Разделим дробь 4/7 на 2:

• 4/7 ÷ 2 = 4/7 * 1/2 = 4/14
• Упростим полученную дробь:
• 4/14 = 2/7

Пример 1: Подмножество дробей с положительным числителем

• 1/2
• 3/4
• 5/6

Во всех перечисленных дробях числитель положителен, так как он представлен положительными числами 1, 3 и 5. Знаменатель дробей может быть любым натуральным числом.

Таким образом, подмножество дробей с положительным числителем представляет собой набор дробей, где числитель положительный и знаменатель может быть любым натуральным числом.

Пример 2: Подмножество дробей с отрицательным числителем

Например, дроби -3/4 и -2/5 являются примерами подмножества дробей с отрицательным числителем. В этих примерах числитель является отрицательным числом, а знаменатель — положительным числом.

Если в дроби числитель и знаменатель одновременно отрицательные, то дробь считается положительной. Например, дроби -1/-2 и -2/-3 считаются положительными, так как числитель и знаменатель одновременно отрицательные.

Подмножество дробей с отрицательным числителем широко используется в математике и в различных областях науки, например, в физике и экономике. Понимание этого понятия помогает решать задачи, связанные с отрицательными долями и отношениями.

Пример 3: Подмножество дробей с отрицательным знаменателем

Дробь: -3/4

В данном случае, знаменатель дроби (-4) является отрицательным числом. Такие дроби также относятся к подмножеству дробей.

Подмножество дробей с отрицательным знаменателем можно записать следующим образом:

Множество дробей = {a/b | a — произвольное число, b — отрицательное число}

Таким образом, все дроби, у которых знаменатель является отрицательным числом, входят в данное подмножество.

Вопрос-ответ:

Что такое подмножество дробей?

Подмножество дробей — это множество, состоящее из дробей, которые удовлетворяют определенному условию или ограничению.

Какие основные понятия связаны с подмножеством дробей?

Основные понятия, связанные с подмножеством дробей, включают понятия обыкновенной дроби, числителя, знаменателя, несократимой дроби и дробей с одинаковыми знаменателями.

Как найти подмножество дробей с определенным числителем?

Для того чтобы найти подмножество дробей с определенным числителем, нужно рассмотреть все дроби, у которых числитель равен данному числу, а знаменатель может быть любым натуральным числом.

Можно ли привести пример подмножества дробей?

Да, можно привести пример подмножества дробей. Например, подмножество дробей, у которых знаменатель равен 2, будет состоять из таких дробей как 1/2, 3/2, 5/2 и так далее.

Как определить, является ли дробь сократимой или несократимой?

Для определения, является ли дробь сократимой или несократимой, нужно проверить, есть ли у числителя и знаменателя общие делители, кроме 1. Если есть, то дробь сократимая, если нет, то дробь несократимая.

Как определить, что дробь является правильной?

Правильная дробь — это дробь, числитель которой меньше знаменателя. Например, дроби 1/2, 3/4, 2/5 являются правильными.

Как определить, что дробь является неправильной?

Неправильная дробь — это дробь, числитель которой больше знаменателя. Например, дроби 3/2, 5/4, 7/5 являются неправильными.

Пример 4: Подмножество дробей с дробными числителями и знаменателями

• 0.5/0.2
• 1.25/0.5
• 3.75/0.25
• 0.8/0.4

В данном примере числитель и знаменатель каждой дроби представлены в виде десятичных дробей. Такие дроби можно представить в виде конечных десятичных дробей или периодических десятичных дробей. Например, дробь 0.5/0.2 равна 2.5, а дробь 3.75/0.25 равна 15.

Подмножество дробей с дробными числителями и знаменателями является частным случаем дробей и представляет собой важный элемент математической теории и практических применений, таких как финансовые расчеты, процентные ставки, доли и т.д.

Видео по теме: