Что такое число в кубе в математике
Содержимое
- 1 Что такое число в кубе в математике
Число в кубе — это результат умножения числа на себя два раза. В математике число в кубе обозначается с помощью верхнего индекса 3. Знание основных свойств чисел в кубе позволяет решать задачи, связанные с объемами, геометрическими фигурами и арифметическими операциями.
В математике число в кубе представляет собой результат возведения числа в третью степень. Это значит, что число умножается на само себя два раза. Например, число 2 в кубе равно 2 * 2 * 2 = 8. Таким образом, число в кубе является произведением трех одинаковых множителей.
Важно отметить, что возведение числа в куб является одной из основных операций в алгебре. Она позволяет нам решать различные задачи, связанные с объемом и геометрическими формами. Например, для вычисления объема куба нужно знать длину его стороны и возвести ее в куб.
Число в кубе имеет несколько особенностей, о которых стоит упомянуть. Во-первых, число в кубе всегда положительное, даже если исходное число было отрицательным. Например, (-2) в кубе равно (-2) * (-2) * (-2) = -8, что является отрицательным числом. Во-вторых, число в кубе может быть использовано для нахождения кубического корня. То есть, если мы знаем число в кубе, мы можем найти исходное число.
Итак, число в кубе представляет собой результат возведения числа в третью степень. Оно имеет несколько особенностей, таких как всегда положительное значение и возможность использования для нахождения кубического корня. Знание и понимание этих особенностей помогает в решении различных задач, связанных с алгеброй и геометрией.
Что такое число в кубе
Число в кубе обладает рядом особенностей:
- Число в кубе всегда положительное, даже если исходное число отрицательное. Например, (-2)^3 = -2 * -2 * -2 = -8.
- Куб числа можно представить в виде объема куба с ребром, равным данному числу. Например, 2^3 = 2 * 2 * 2 = 8, что соответствует объему куба с ребром 2.
- Число в кубе растет быстрее, чем само число. Например, 10^3 = 10 * 10 * 10 = 1000, в то время как 10^2 = 10 * 10 = 100.
Число в кубе встречается в различных областях математики и естественных науках, включая алгебру, геометрию, физику и другие.
Видео по теме:
Способы возведения числа в куб
Число в куб можно возвести с помощью различных методов. Рассмотрим несколько основных способов:
- Умножение числа на само себя два раза. Например, чтобы возвести число 2 в куб, нужно умножить его на себя два раза: 2 * 2 * 2 = 8.
- Использование свойства куба суммы. Если нужно возвести сумму двух чисел в куб, можно сначала возвести каждое число в куб, а затем сложить результаты. Например, чтобы возвести сумму чисел 3 и 4 в куб, нужно сначала возвести каждое число в куб: 3 * 3 * 3 = 27 и 4 * 4 * 4 = 64, а затем сложить результаты: 27 + 64 = 91.
- Применение формулы разности кубов. Формула разности кубов гласит, что разность кубов двух чисел можно представить в виде произведения разности этих чисел и суммы их квадратов плюс произведение квадратов этих чисел. Например, чтобы возвести разность чисел 5 и 2 в куб, можно воспользоваться формулой: (5 — 2) * ((5 * 5) + (2 * 2) + (5 * 2)) = 3 * (25 + 4 + 10) = 3 * 39 = 117.
Это лишь некоторые из способов возведения числа в куб. В математике существует и другие методы, которые могут быть применены в зависимости от конкретной задачи или условий.
Основные свойства числа в кубе
Основные свойства числа в кубе:
| Сложение | Сумма двух чисел в кубе равна произведению суммы этих чисел на их разность, умноженное на сумму квадратов этих чисел. |
| Вычитание | Разность двух чисел в кубе равна произведению разности этих чисел на сумму квадратов этих чисел, умноженное на обратную величину суммы этих чисел. |
| Умножение | Произведение двух чисел в кубе равно кубу произведения этих чисел. |
| Деление | Частное двух чисел в кубе равно кубу частного этих чисел. |
| Возведение в степень | Число в кубе можно возвести в любую степень, просто умножив число на само себя нужное количество раз. |
Зная основные свойства чисел в кубе, можно проводить различные операции с этими числами и решать математические задачи, связанные с кубическими числами.
Вопрос-ответ:
Что такое число в кубе?
Число в кубе — это число, возведенное в третью степень, то есть умноженное на себя два раза. Например, число 3 в кубе равно 3 * 3 * 3 = 27.
Каким образом можно вычислить число в кубе?
Для того чтобы вычислить число в кубе, необходимо умножить это число само на себя два раза. Например, чтобы вычислить 4 в кубе, нужно выполнить следующее вычисление: 4 * 4 * 4 = 64.
Какие особенности свойственны числам в кубе?
Числа в кубе обладают несколькими особенностями. Одна из них заключается в том, что все числа в кубе всегда положительные, независимо от знака исходного числа. Кроме того, числа в кубе растут быстро с увеличением исходного значения.
Можно ли найти кубический корень числа?
Да, можно найти кубический корень числа, который является числом, возведенным в куб. Например, кубический корень из 27 равен 3, так как 3 * 3 * 3 = 27.
Примеры чисел в кубе
В математике число в кубе представляет собой результат умножения числа на себя два раза. Например, 2 в кубе равно 2 * 2 * 2 = 8, а 3 в кубе равно 3 * 3 * 3 = 27.
Ниже приведены некоторые примеры чисел, возведенных в куб:
- 1 в кубе = 1 * 1 * 1 = 1
- 2 в кубе = 2 * 2 * 2 = 8
- 3 в кубе = 3 * 3 * 3 = 27
- 4 в кубе = 4 * 4 * 4 = 64
- 5 в кубе = 5 * 5 * 5 = 125
Возведение чисел в куб является основным способом получения чисел, которые можно представить в виде объемов кубов. Это широко используется в различных областях науки и инженерии.
Значение числа в кубе в геометрии
В геометрии число в кубе используется для определения объема куба.
Куб — это геометрическое тело, у которого все стороны равны друг другу и прямые углы между смежными сторонами.
Чтобы найти объем куба, необходимо возвести длину одной из его сторон в куб. Формула для расчета объема куба выглядит следующим образом:
| Объем куба: | V = a3 |
Где «V» — объем куба, «a» — длина стороны куба.
Зная длину стороны куба, можно легко найти его объем, возведя эту длину в куб.
Значение числа в кубе в геометрии является одной из основных характеристик куба и позволяет рассчитывать его объем.
Число в кубе в физике
Число в кубе, или третья степень числа, играет важную роль в физике. Во многих физических законах и уравнениях третья степень числа встречается как результат возведения в куб некоторой физической величины.
Например, в законе всемирного тяготения Ньютона третья степень расстояния между двумя телами определяет силу взаимодействия между ними. В уравнении Гаусса для электрического поля третья степень расстояния от точечного заряда определяет величину поля в данной точке пространства.
Также числа в кубе часто используются для описания объемов и плотности. Например, в законе Архимеда третья степень радиуса тела определяет объем вытесненной им воды. В формуле плотности вещества третья степень линейного размера определяет объемное распределение массы.
Числа в кубе в физике позволяют ученым более точно описывать и предсказывать физические явления и взаимодействия. Они играют важную роль в различных областях физики, включая механику, электродинамику, астрономию и многие другие.
Роль числа в кубе в экономике

Одной из основных областей, где используется число в кубе, является анализ экономических данных. Например, при анализе временных рядов, третья степень числа может использоваться для моделирования трендов и предсказания будущих значений. Аналитики могут применять методы регрессионного анализа, включая полиномиальную регрессию, чтобы оценить влияние факторов на экономические показатели.
В экономике число в кубе может быть также использовано при расчете объема производства или потребления. Например, если требуется определить объем производства товаров или услуг на основе известных данных, можно использовать число в кубе для аппроксимации этого объема. Это может быть полезно при прогнозировании спроса на товары или планировании бизнес-стратегии.
Еще одним примером использования числа в кубе в экономике является анализ риска и доходности инвестиций. При оценке доходности или потенциальных потерь от инвестиций аналитики могут использовать третью степень числа для моделирования вариантов развития событий. Это может помочь принять обоснованные решения и учесть возможные риски.
Таким образом, число в кубе играет важную роль в экономике и финансовой аналитике. Оно может быть использовано для моделирования трендов, прогнозирования будущих значений, расчета объема производства или потребления, а также анализа риска и доходности инвестиций. Понимание и использование этого математического понятия помогает экономистам и аналитикам принимать обоснованные решения и делать точные прогнозы в сфере экономики и финансов.
Применение числа в кубе в программировании
Объем куба вычисляется по формуле: V = a^3, где a — длина ребра куба. Данная формула позволяет получить объем куба при известной длине его ребра.
Кроме вычисления объема куба, число в кубе может использоваться для решения различных математических задач. Например, в алгоритмах шифрования и хеширования используется возведение числа в куб. Также, в некоторых алгоритмах оптимизации и анализа данных применяется возведение числа в куб для выполнения различных вычислений.
В программировании возведение числа в куб может быть реализовано с помощью операции умножения. Например, для возведения числа x в куб можно использовать следующую формулу: x * x * x. Также, существуют специальные функции и операторы, позволяющие возводить число в куб.
Применение числа в кубе в программировании позволяет решать различные задачи, связанные с вычислениями и анализом данных. Возведение числа в куб является одной из основных операций, которая может быть использована для выполнения различных математических операций и алгоритмов.

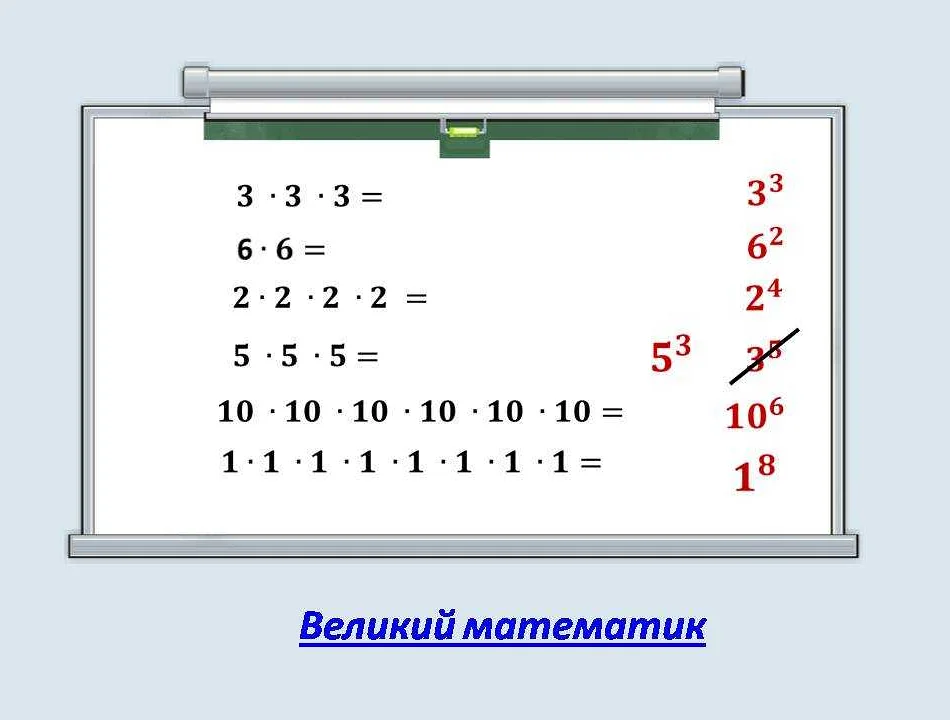

Статья очень информативная и понятная. Она хорошо объясняет, что такое число в кубе и как его определить. Мне понравилось, что автор дал примеры расчетов и показал, как можно применить это знание в реальной жизни. Числа в кубе имеют свои особенности, и их изучение помогает лучше понять математику. Статья легко читается и интересна. Я узнал много нового и буду рад прочитать еще статьи на эту тему. Большое спасибо!