Что такое числовая функция в математике
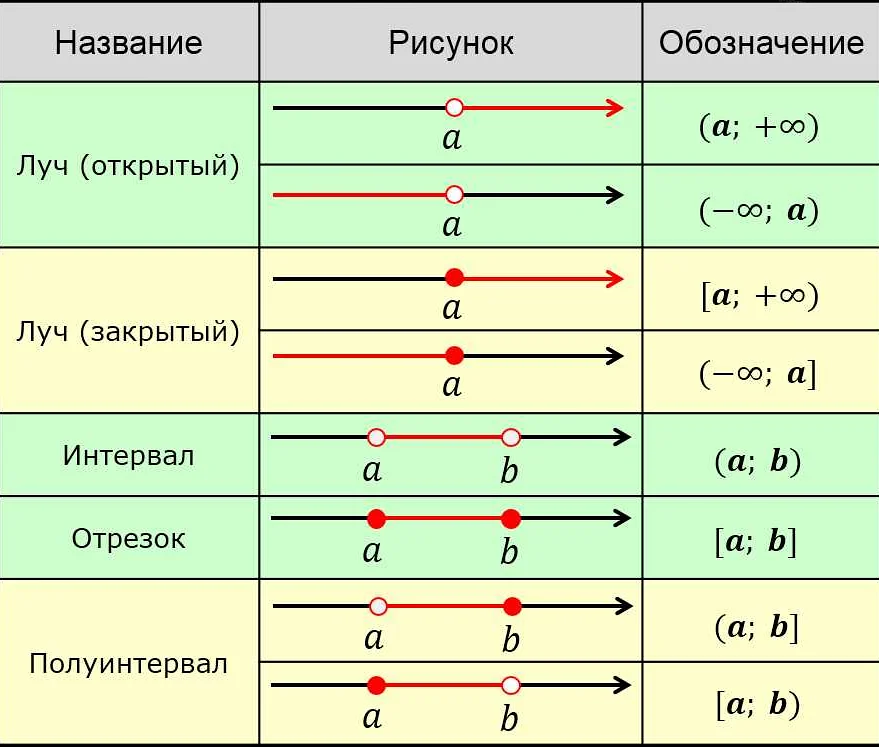
Содержимое
Числовая функция в математике — это отображение, которое каждому элементу из одного множества сопоставляет элемент из другого множества чисел. Узнайте, как они используются для моделирования и анализа различных явлений и процессов в математике и естественных науках.
Числовая функция является одним из основных понятий в математике. Это математический объект, который сопоставляет каждому элементу из одного числового множества элемент из другого числового множества. Определение числовой функции включает в себя два основных компонента: область определения и область значений.
Область определения функции — это множество всех элементов, для которых функция имеет определение. Область значений функции — это множество всех элементов, которые могут быть получены в результате применения функции к элементам области определения. Числовая функция может быть представлена в виде аналитического выражения, графика или таблицы значений.
Особенностью числовой функции является то, что каждому элементу из области определения соответствует только один элемент из области значений. Это означает, что функция должна быть «однозначной». Если функция соответствует нескольким элементам из области определения одинаковым значениям из области значений, она называется «многозначной».
Примерами числовых функций могут служить такие математические объекты, как линейная функция, квадратичная функция, тригонометрические функции (синус, косинус и тангенс) и логарифмическая функция. Линейная функция, например, задается аналитическим выражением вида y = ax + b, где a и b — константы и x — переменная. График линейной функции представляет собой прямую линию на плоскости. Квадратичная функция, в свою очередь, задается аналитическим выражением вида y = ax^2 + bx + c, где a, b и c — константы и x — переменная. График квадратичной функции представляет собой параболу.
Что такое числовая функция

Числовая функция может быть представлена в виде графика или аналитическим способом, используя алгебраическое выражение. График числовой функции представляет собой геометрическое представление связи между значениями входных и выходных чисел. Аналитическое выражение числовой функции позволяет определить правило преобразования чисел.
Числовая функция может иметь различные свойства, такие как монотонность, ограниченность, периодичность и др. Монотонность функции определяет изменение ее значений при изменении входных чисел. Ограниченность функции говорит о том, что значения функции ограничены сверху или снизу. Периодичность функции означает, что функция повторяется через определенный интервал значений.
Примеры числовых функций включают линейные функции, квадратичные функции, показательные функции, тригонометрические функции и др. Линейная функция представляет собой прямую линию на графике и имеет аналитическое выражение вида y = kx + b, где k и b — константы. Квадратичная функция имеет график в форме параболы и аналитическое выражение вида y = ax^2 + bx + c, где a, b и c — константы.
Числовые функции играют важную роль в математике и науке, используя их мы можем анализировать и предсказывать различные явления и процессы.
Видео по теме:
Особенности числовых функций
Числовые функции в математике имеют свои особенности, которые важно учитывать при их исследовании и применении:
1. Определенность значений: Каждому аргументу числовой функции соответствует одно определенное значение функции. Это означает, что каждый аргумент имеет свой уникальный результат.
2. Область определения: Числовая функция определена только для тех значений аргумента, для которых существует корректное значение функции. Область определения может быть ограничена или неограничена в зависимости от конкретной функции.
3. Область значений: Область значений числовой функции — это множество всех возможных значений, которые может принимать функция. Область значений может быть ограничена или неограничена и зависит от правил функции.
4. График функции: График числовой функции — это графическое представление всех ее значений. График может быть линейным, параболическим, экспоненциальным и т. д. График функции позволяет наглядно представить ее поведение и свойства.
5. Непрерывность: Числовая функция называется непрерывной, если ее график не имеет разрывов или пропусков. Непрерывность функции важна при ее анализе и решении уравнений.
6. Отношение между аргументами и значениями: Числовая функция может быть однозначной, когда каждому значению аргумента соответствует только одно значение функции, или многозначной, когда одному значению аргумента соответствует несколько значений функции.
7. Четность и нечетность: Некоторые числовые функции обладают свойствами четности или нечетности. Функция называется четной, если выполняется условие f(-x) = f(x) для любого x из области определения. Функция называется нечетной, если выполняется условие f(-x) = -f(x) для любого x из области определения.
8. Монотонность: Числовая функция называется монотонной, если она либо всюду возрастает, либо всюду убывает. Монотонность функции определяет ее поведение и изменение значений в зависимости от изменения аргумента.
9. Производная и интеграл: Производная числовой функции позволяет определить ее скорость изменения и найти касательную к ее графику в конкретной точке. Интеграл числовой функции позволяет найти площадь под ее графиком или найти значение функции по ее производной.
Изучение и понимание этих особенностей числовых функций позволяет проводить более глубокий анализ и решение задач, связанных с ними.
Примеры числовых функций
Числовые функции могут принимать различные формы и использоваться для решения разнообразных задач. Ниже приведены некоторые примеры числовых функций:
1. Функция сложения: Это простейший пример числовой функции, которая складывает два числа и возвращает результат. Например, функция f(x, y) = x + y складывает числа x и y и возвращает их сумму.
2. Функция умножения: Другой пример числовой функции, которая умножает два числа и возвращает результат. Например, функция g(x, y) = x * y умножает числа x и y и возвращает их произведение.
3. Функция возведения в степень: Эта функция принимает число и степень, в которую нужно возвести это число, и возвращает результат. Например, функция h(x, n) = x^n возводит число x в степень n и возвращает результат.
4. Функция сравнения: Это функция, которая принимает два числа и сравнивает их между собой, возвращая истину или ложь в зависимости от результата сравнения. Например, функция k(x, y) = x > y сравнивает числа x и y и возвращает true, если x больше y, и false в противном случае.
5. Функция модуля числа: Эта функция принимает число и возвращает его абсолютное значение (модуль). Например, функция m(x) = |x| возвращает абсолютное значение числа x.
Это лишь некоторые примеры числовых функций, и их много различных видов и форм. Числовые функции широко используются в математике, физике, экономике и других областях для моделирования и решения разнообразных задач.
Линейная функция
Особенностью линейной функции является то, что график этой функции представляет собой прямую линию на координатной плоскости.
Коэффициент a в формуле определяет угловой коэффициент прямой — он указывает, насколько быстро растет или убывает значение функции при изменении аргумента. Если a > 0, то прямая возрастает, а если a < 0, то прямая убывает. Если a = 0, то прямая горизонтальна и функция не зависит от аргумента.
Свободный член b в формуле определяет смещение прямой по вертикали. Если b > 0, то прямая смещается вверх, а если b < 0, то прямая смещается вниз. Если b = 0, то прямая проходит через начало координат.
Примеры линейных функций:
ФункцияФормулаГрафик
| Функция возрастает | f(x) = 2x + 1 |  |
| Функция убывает | f(x) = -3x + 2 |  |
| Горизонтальная функция | f(x) = 4 |  |
| Функция со смещением | f(x) = x + 3 |  |
Квадратичная функция
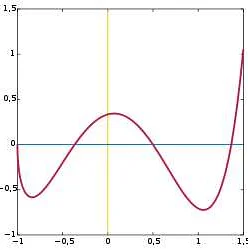
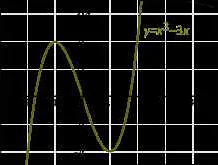
Особенностью квадратичной функции является то, что график этой функции представляет собой параболу. Ее форма и положение зависят от значений коэффициентов a, b и c.
Коэффициент a определяет направление открытия параболы и ее степень изогнутости. Если a > 0, парабола открывается вверх и имеет минимум. Если a < 0, парабола открывается вниз и имеет максимум.
Коэффициенты b и c влияют на положение параболы на плоскости. Коэффициент b определяет сдвиг параболы по оси x, а коэффициент c – сдвиг по оси y.
Примеры квадратичных функций:
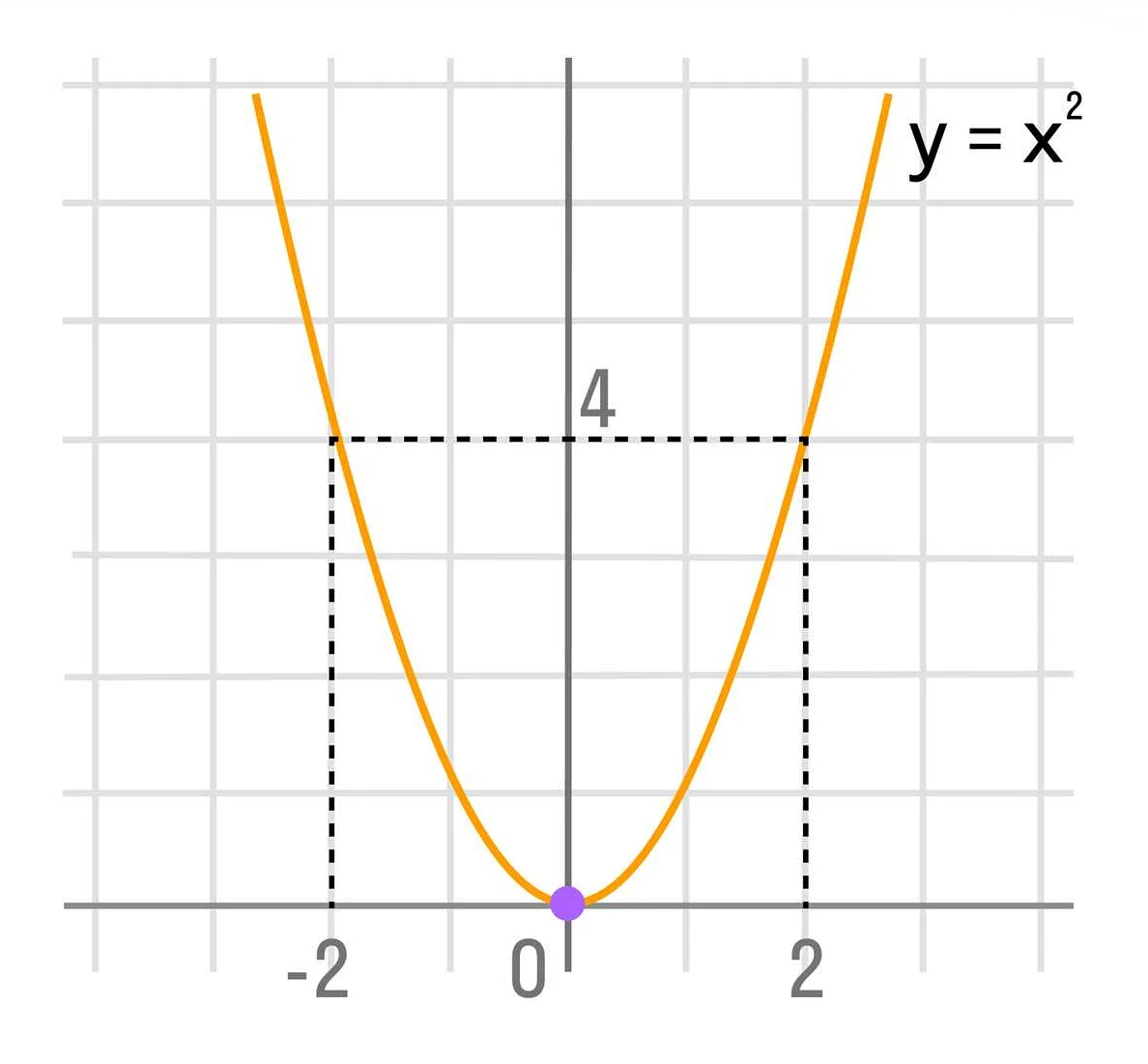
1. f(x) = x^2 – это простейшая квадратичная функция, график которой представляет собой параболу, открывающуюся вверх и с вершиной в начале координат.
2. f(x) = -2x^2 + 3x + 1 – это квадратичная функция, график которой открывается вниз и имеет максимум. Сдвиг по оси x составляет 3 единицы вправо, а по оси y – 1 единицу вверх.
3. f(x) = x^2 — 4 – это квадратичная функция, график которой открывается вверх и имеет минимум. Сдвиг по оси x отсутствует, а сдвиг по оси y составляет -4 единицы вниз.
Экспоненциальная функция
Особенностью экспоненциальной функции является то, что ее значение растет или убывает очень быстро при изменении значения переменной x. Если основание a больше 1, то функция увеличивается с ростом x. Если основание меньше 1, то функция уменьшается. Чем больше разница между основанием и 1, тем быстрее функция увеличивается или убывает.
Экспоненциальные функции широко применяются в различных областях, таких как физика, экономика, биология и информатика. Они описывают рост и убывание популяции, распределение ресурсов, распад радиоактивных элементов и многое другое.
Некоторые примеры экспоненциальных функций:
- f(x) = 2x — экспоненциальная функция с основанием 2, которая растет с ростом x.
- f(x) = 0.5x — экспоненциальная функция с основанием 0.5, которая убывает с ростом x.
- f(x) = ex — экспоненциальная функция с основанием e (приближенное значение 2.71828), которая растет очень быстро с ростом x.
Тригонометрическая функция
Основные тригонометрические функции включают синус, косинус, тангенс, котангенс, секанс и косеканс. Эти функции определены для всех действительных чисел и обладают различными свойствами и графиками.
Синус (sin) определяется как отношение противоположного катета к гипотенузе в прямоугольном треугольнике. Косинус (cos) определяется как отношение прилежащего катета к гипотенузе. Тангенс (tan) равен отношению синуса косинуса. Котангенс (cot) равен обратному отношению тангенса. Секанс (sec) определяется как обратное отношение косинуса, а косеканс (cosec) равен обратному отношению синуса.
Тригонометрические функции имеют периодические свойства и повторяются через определенные интервалы. Они также связаны с геометрическими фигурами, такими как окружность, и используются для решения различных задач, связанных с геометрией и физикой.
Примеры применения тригонометрических функций включают измерение углов, нахождение высоты и длины сторон треугольников, моделирование колебаний и волн, а также решение уравнений, связанных с периодическими явлениями.
Важно отметить, что для работы с тригонометрическими функциями в математических пакетах и языках программирования обычно используются радианы вместо градусов, так как радианы обеспечивают более удобные вычисления и связи между различными тригонометрическими функциями.
Обратная функция
Для того чтобы функция имела обратную функцию, она должна быть биективной, то есть каждому значению y из области значений функции f(x) должно соответствовать единственное значение x из области определения функции f(x).
Обратная функция может быть представлена графически с помощью отражения графика исходной функции относительно линии y=x. Точки пересечения графиков функции и ее обратной функции являются симметричными относительно этой линии.
Важно отметить, что не все функции имеют обратные функции. Для того чтобы функция имела обратную функцию, она должна быть строго монотонной на своей области определения. Например, функция y = x2 не имеет обратной функции, так как она не является строго монотонной.
Примеры функций с обратными функциями:
- Линейная функция y = kx + b, где k ≠ 0, имеет обратную функцию y = (x — b) / k.
- Экспоненциальная функция y = ax, где a > 0 и a ≠ 1, имеет обратную функцию y = loga(x).
- Тригонометрическая функция y = sin(x) на отрезке [-π/2, π/2] имеет обратную функцию y = arcsin(x).
Вопрос-ответ:
Что такое числовая функция?
Числовая функция в математике — это функция, которая сопоставляет каждому элементу из одного числового множества элемент из другого числового множества. В более простых словах, это правило, которое превращает числа из одного множества в числа из другого множества.
Какие особенности имеют числовые функции?
Числовые функции обладают несколькими особенностями. Во-первых, каждому элементу из одного числового множества соответствует только один элемент из другого числового множества. Во-вторых, числовые функции могут быть определены на различных интервалах числовой прямой или на всей числовой прямой. В-третьих, числовые функции могут быть линейными (график функции — прямая линия) или нелинейными (график функции — кривая линия).
Какие примеры числовых функций вы можете привести?
Примерами числовых функций могут служить: линейные функции вида y = kx + b, где k и b — константы; квадратные функции вида y = ax^2 + bx + c, где a, b и c — константы; тригонометрические функции, такие как синус, косинус и тангенс; и много других функций, которые могут быть определены на разных интервалах числовой прямой.
Какова роль числовых функций в математике?
Числовые функции играют важную роль в математике, так как они позволяют описывать и анализировать различные явления и процессы в нашем мире с помощью чисел. Они используются в различных областях, таких как физика, экономика, статистика и многих других. Числовые функции позволяют моделировать реальные ситуации и прогнозировать результаты на основе имеющихся данных.


Очень интересная статья! Я всегда любила математику, и числовые функции — одна из моих самых любимых тем. Очень хорошо, что вы объяснили определение числовой функции и ее особенности. Я согласна с тем, что числовая функция — это правило, которое связывает каждое число из одного множества с числом из другого множества. Примеры, которые вы привели, очень наглядно иллюстрируют это. Я обязательно поделюсь этой статьей со своими друзьями, которые тоже увлекаются математикой. Спасибо за интересную и познавательную статью!