Что изучает математическое моделирование: основные аспекты и применения
Содержимое
- 1 Что изучает математическое моделирование: основные аспекты и применения
- 1.1 Основные принципы математического моделирования
- 1.2 Математические методы в моделировании
- 1.3 Области применения математического моделирования
- 1.4 Элементы системы моделирования
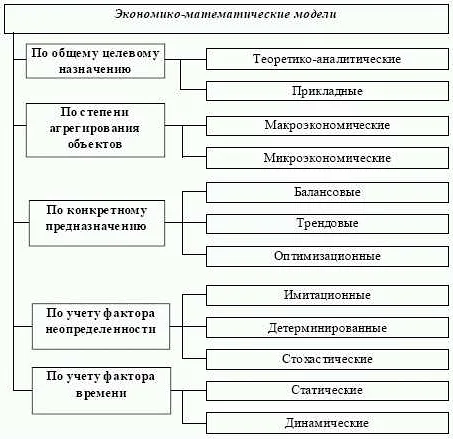
- 1.5 Классификация математических моделей
- 1.6 Иерархия моделей
- 1.7 Виды моделей
- 1.8 Масштабирование моделей
- 1.9 Видео по теме:
- 1.10 Вопрос-ответ:
- 1.10.0.1 Какова цель математического моделирования?
- 1.10.0.2 Какие задачи решает математическое моделирование?
- 1.10.0.3 Какие методы используются в математическом моделировании?
- 1.10.0.4 Какова роль математического моделирования в современном мире?
- 1.10.0.5 Какие проблемы могут возникнуть при математическом моделировании?
- 1.10.0.6 Какая роль математических моделей в научных исследованиях?
- 1.10.0.7 Как можно улучшить точность математической модели?
- 1.11 Примеры успешного применения математического моделирования
- 1.12 Ограничения математического моделирования
Статья расскажет, что изучает математическое моделирование, его роль и применение в различных областях, таких как физика, экономика, биология, информатика и другие. Вы узнаете, какие методы и алгоритмы используются для создания и анализа математических моделей.
Математическое моделирование – это метод научных исследований, основанный на использовании математических моделей. Математическая модель – это упрощенное описание объекта или процесса, представленное в виде математических формул. Модель может быть создана для различных областей знаний: от физики и химии до экономики и социологии.
Цель математического моделирования – описать и объяснить явления реального мира на уровне математических формул и графиков. Это помогает исследователям лучше понимать механизмы происходящих процессов и предсказывать их будущее развитие. Моделирование также позволяет проводить эксперименты «виртуально», что может быть полезным в различных сферах промышленности и науки.
Изучение математического моделирования требует знаний в таких областях математики, как дифференциальные уравнения, статистика, теория вероятности и оптимизация. На практике модели строятся с использованием различных программных средств, таких как MATLAB, Maple или Python. Все это делает математическое моделирование очень важным инструментом в научных и технических исследованиях и повседневной жизни.
Основные принципы математического моделирования
Математическое моделирование – это процесс создания математических моделей реальных явлений, ситуаций и процессов. Оно осуществляется на основе определенных принципов, которые позволяют создавать точные и надежные математические модели.
Один из основных принципов математического моделирования – это приближение. В большинстве случаев невозможно учесть все факторы, оказывающие влияние на изучаемый процесс. Поэтому необходимо выбрать только наиболее значимые факторы и создать модель на основе упрощенных условий.
Второй важный принцип – это формализация и математическое описание процесса. Все процессы и явления должны быть описаны с помощью формул, функций и уравнений, которые смогут точно описать структуру и зависимости между различными факторами.
Третий принцип – это верификация и валидация модели. Это значит, что созданную модель необходимо проверить на соответствие реальности. Для этого проводятся эксперименты и сравниваются результаты моделирования с реальной ситуацией. Если модель показывает точные результаты, то она считается верифицированной и валидной.
Еще один принцип – это анализ результатов моделирования. После того, как модель протестирована и верифицирована, необходимо проанализировать результаты и оценить их точность и достоверность. Это позволяет сделать выводы о том, каким образом улучшить модель и повысить точность результатов.
Таким образом, основные принципы математического моделирования позволяют создавать точные и надежные модели реальных процессов и явлений. Их использование позволяет сократить экспериментальные затраты, ускорить процесс разработки новых технологий и улучшить качество принимаемых решений.
Математические методы в моделировании
Математическое моделирование является процессом создания математических моделей, которые отображают системы и процессы в реальном мире. Задача математического моделирования заключается в том, чтобы сделать предсказания о поведении системы на основе изучения ее свойств и взаимодействия с окружающей средой.
Для того чтобы создать математическую модель, необходимо использовать математические методы. Они позволяют описать систему в терминах математических уравнений и формул. Многие из этих методов включают в себя анализ и преобразование данных, а также использование статистических методов для оценки результатов.
Один из наиболее распространенных математических методов, используемых в моделировании, — это дифференциальные уравнения. Они позволяют описывать и анализировать изменения, которые происходят в системе с течением времени. Другим примером является статистический анализ, который используется для изучения распределения и свойств данных и для создания прогнозов будущих событий.
Современные вычислительные технологии также широко используются в математическом моделировании. Использование компьютерных программ и алгоритмов позволяет смоделировать процессы, которые были бы невозможны для анализа вручную. К примеру, численные методы позволяют решать системы уравнений, которые вручную решить невозможно в силу их сложности или размеров.
Таким образом, математические методы играют важную роль в моделировании различных систем, и позволяют создавать точные прогнозы и определять наиболее эффективные стратегии действий.
Области применения математического моделирования
Математическое моделирование является важным инструментом для прогнозирования и оптимизации различных процессов и явлений в различных областях:
- Физика: математическое моделирование помогает предсказывать поведение объектов на микро и макроуровнях, таких как элементарные частицы, атомы, молекулы, облака и атмосфера.
- Биология: с помощью математического моделирования можно изучать биологические процессы, которые сложно наблюдать вживую, например, процессы митоза, основные механизмы роста и развития организмов.
- Экономика: математическое моделирование позволяет предсказывать изменения рыночных тенденций, оптимизировать портфели инвестиций, оценить риски и многое другое.
- Инженерия: математическое моделирование используется для проектирования сложных систем, оптимизации производственных процессов, конструирования новых устройств и многого другого.
- Социология: математическое моделирование позволяет изучать социальные процессы и предсказывать их развитие, такие как изменение демографических структур, миграция и социальная мобильность.
Эти области применения не являются исчерпывающим списком, поскольку математическое моделирование может быть использовано практически в любой области для решения сложных задач.
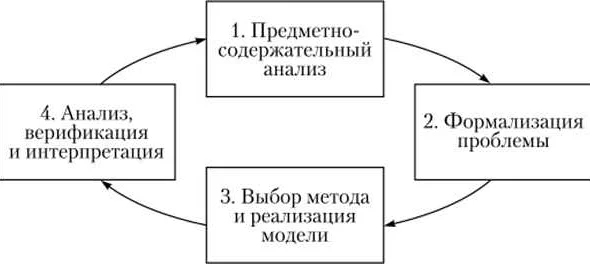
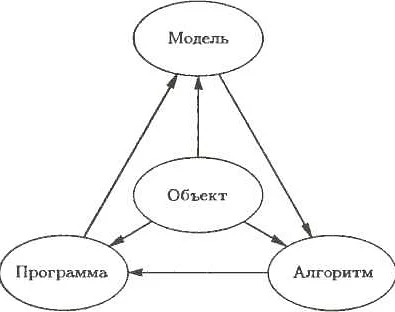
Элементы системы моделирования
Математическое моделирование — это процесс создания математической модели объекта или системы с целью изучения их свойств и поведения.
Элементы системы моделирования включают в себя:
- Объект моделирования, для которого создается математическая модель.
- Математическая модель, которая описывает поведение и свойства объекта моделирования.
- Методы моделирования, используемые для решения математических задач, связанных с моделью.
- Программное обеспечение, необходимое для создания и анализа математических моделей.
Основными задачами математического моделирования является анализ и прогнозирование поведения и свойств объектов и систем, а также оптимизация работы их компонентов. Поэтому элементы системы моделирования должны быть тесно связаны между собой и образовывать комплексную систему для достижения поставленных целей.
При математическом моделировании необходимо учитывать достоверность и точность модели, а также сопоставимость ее результатов с реальными данными. Поэтому создание математических моделей считается одним из важнейших инструментов для исследования и оптимизации различных процессов и систем.
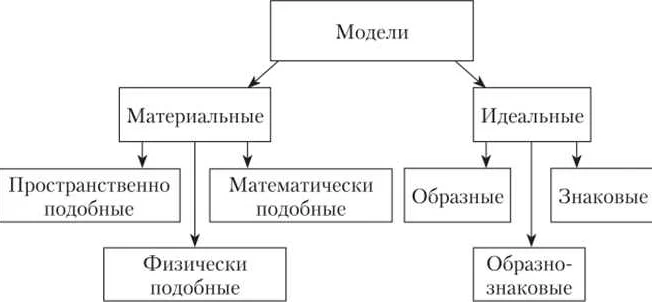
Классификация математических моделей
Математическое моделирование – это процесс создания моделей для научных и инженерных исследований. Математические модели могут быть классифицированы по различным критериям. Рассмотрим несколько типов таких моделей:
- Аналитические модели представляют выражение в аналитической форме. Эти модели используют математические уравнения для описания динамики системы. Примером такой модели может быть закон Ньютона или уравнение Шредингера в квантовой механике.
- Численные модели используют численные значения для описания системы. Это методы численного анализа, которые моделируют систему, используя численные алгоритмы. Примеры численных моделей включают метод конечных элементов для решения дифференциальных уравнений или метод Монте-Карло для анализа вероятностных процессов.
- Физические модели моделируют физические процессы в реальном мире. Они представляют реальные объекты в масштабе в виде модели. Примеры физических моделей – это компьютерное моделирование работы двигателя, ветровые тоннели и модели пластмассовых изделий.
- Статистические модели описывают вероятностные связи в системе. Эти модели используют статистические методы для вычисления вероятностных значений и могут быть использованы для прогнозирования.
Классификация моделей в математическом моделировании помогает более точно определить методы и инструменты для решения поставленной задачи. Каждый тип модели имеет свои преимущества и недостатки, поэтому важно выбрать тот, который лучше всего подходит для задачи в русле теоретического исследования или для определения практических решений.
Иерархия моделей
Математическое моделирование — это процесс создания математических моделей для изучения систем. Одна модель может быть упрощенной версией реальной системы, а другая — комплексной моделью с множеством показателей, условий и переменных. Построение иерархии моделей является важным этапом в изучении систем.
На вершине иерархии находится самая упрощенная модель, которая используется для первоначального анализа системы. Она может содержать только несколько переменных и учитывать только основные факторы, влияющие на систему. Последующие модели подробнее описывают различные элементы системы и учитывают большее количество факторов.
Каждая следующая модель в иерархии является более сложной и подробной, чем предыдущая. Для каждой модели требуется больше данных и ресурсов, но она также способна более точно описывать систему. Наиболее сложные модели могут учитывать многофакторные взаимодействия и предсказывать долгосрочное поведение системы.
Иерархия моделей позволяет ученым изучать систему постепенно, начиная с простых моделей и продвигаясь к более сложным. Это позволяет получить более полное понимание системы и разработать более точные прогнозы ее поведения в будущем.
Виды моделей
Математическое моделирование является универсальным инструментом, который позволяет решать исключительно широкий круг задач. В зависимости от конкретной ситуации, разрабатываются различные типы моделей, которые могут быть использованы для анализа и прогнозирования процессов или явлений. Рассмотрим некоторые из наиболее распространённых видов моделей:
- Аналитические модели – это модели, которые основаны на математических уравнениях и формулах, которым присуща точность и строгость. Они широко используются для описания процессов природы, экономики и социума.
- Статистические модели – это модели, которые используются при обработке экспериментальных данных. Они позволяют оценить взаимосвязь между переменными и установить зависимости.
- Эмпирические модели – это модели, которые основаны на опыте и экспериментах. Они используются в тех случаях, когда нет возможности сформировать математическую модель или она не описывает процесс полностью.
- Имитационные модели – это модели, которые строятся на основе имитации процессов реального мира в компьютерных средах. Они находят широкое применение при моделировании сложных систем.
- Гибридные модели – это модели, которые являются комбинацией нескольких видов моделей. Они используются в случаях, когда необходимо учесть различные факторы и переменные при анализе процессов.
Применение того или иного типа математической модели зависит от целей, которые ставит научное сообщество. Чтобы выбрать подходящую модель, необходимо тщательно изучить исследуемый объект и определить, какие перспективы имеются в моделировании данного процесса.
Масштабирование моделей
Одной из важных задач математического моделирования является создание адекватной модели, которая бы точно отражала реальность. Но после создания модели возникает вопрос её масштабирования.
Масштабирование моделей может производиться в различных направлениях. Например, можно увеличить масштаб карты, чтобы изучать крупномасштабные процессы. Также можно изменять масштаб объектов в модели. Например, уменьшить размеры атомов в химической модели для уменьшения сложности вычислений.
Но не всегда масштабирование модели можно считать без последствий. Иногда при изменении масштаба изменяется и сам процесс в модели. Например, рост деревьев зависит от многих факторов, таких как освещение, температура, влажность и т.д., и не всегда можно просто уменьшить масштаб модели, не учитывая этих факторов.
Поэтому масштабирование моделей требует дополнительного внимания и анализа, чтобы не допустить искажения результатов. Кроме того, необходимо учитывать ограничения вычислительной техники и времени на расчёты — чем больше масштаб, тем больше вычислительных ресурсов необходимо.
Видео по теме:
Вопрос-ответ:
Какова цель математического моделирования?
Основная цель математического моделирования — описать реальные явления с помощью математических моделей и предсказать их поведение в различных условиях.
Какие задачи решает математическое моделирование?
Математическое моделирование решает различные задачи, такие как оптимизация производства, расчеты надежности систем, прогноз погоды, моделирование финансовых рынков и многое другое.
Какие методы используются в математическом моделировании?
В математическом моделировании используются различные методы, такие как дифференциальные уравнения, методы монте-карло, методы численного интегрирования и т.д.
Какова роль математического моделирования в современном мире?
Математическое моделирование является неотъемлемой частью современного мира. Оно используется в науке, технике, медицине, бизнесе и многих других областях для решения различных задач и оптимизации процессов.
Какие проблемы могут возникнуть при математическом моделировании?
При математическом моделировании могут возникнуть различные проблемы, такие как неточность данных, сложность моделирования сложных систем, неизвестность параметров модели и т.д.
Какая роль математических моделей в научных исследованиях?
Математические модели используются для описания исследуемых явлений в науке. Они позволяют изучать эти явления, создавать гипотезы и предсказывать их поведение в различных условиях. Тем самым математические модели играют важную роль в научных исследованиях.
Как можно улучшить точность математической модели?
Для улучшения точности математической модели необходимо использовать более точные данные, учитывать больше параметров и проводить анализ результатов моделирования. Также можно использовать новые методы моделирования и настраивать параметры модели.
Примеры успешного применения математического моделирования
Математическое моделирование успешно применяется в различных областях науки, техники и экономики. Одним из наиболее известных примеров является использование моделей в прогнозировании погоды. С помощью математических методов ученые создают модели, которые позволяют предсказать изменение температуры, давления, скорости ветра и других параметров атмосферы.
Еще одним важным примером применения математического моделирования является проектирование новых автомобилей. С помощью компьютерных программ и математических моделей инженеры могут предсказать, как изменится поведение автомобиля при изменении его конструкции или технических характеристик.
В экономике математическое моделирование используется для прогнозирования рыночных тенденций, оптимизации процессов производства и принятия управленческих решений. Например, с помощью математических моделей можно определить оптимальные цены на товары, чтобы достичь максимальной прибыли при заданных условиях конкуренции и спроса на рынке.
В медицине математическое моделирование применяется для изучения биологических процессов, прогнозирования распространения заболеваний и разработки новых методов лечения. Например, математические модели могут помочь исследовать эффективность новых лекарств, которые еще не были испытаны на людях, или предсказать, как поведет себя определенный вирус при контакте с организмом.
В искусстве математическое моделирование стремительно становится важным инструментом. Так, специализированные программы смогли помочь художникам и производителям фильмов создавать реалистичные трехмерные модели, соединяя математику и искусство.
В общем, примеры применения математического моделирования распространяются по многим областям науки и технологии, предоставляют возможности для более четкого и понятного изучения окружающего мира и решения сложных задач.
Ограничения математического моделирования
Математическое моделирование — это мощный инструмент, который позволяет создавать абстрактные модели реальных процессов и явлений. Однако, при этом следует учитывать и ограничения этого метода, чтобы не допустить ошибок в исследованиях и построении прогнозов.
1. Упрощение моделей
Из-за сложности и многообразия реальных процессов, часто применяются упрощенные модели, которые не учитывают все факторы и нюансы. Такие модели могут привести к неточным результатам, а иногда и к ошибочным выводам.
2. Ограничения точности измерения данных
В работе с математическими моделями необходимо иметь точные данные, однако на практике все сведения не всегда доступны и не всегда измеряются с необходимой точностью. Это провоцирует ошибки при построении моделей и ухудшает их точность и качество.
3. Невозможность учесть все факторы
Реальные процессы и явления невозможно учесть в модели в точности, ввиду его многолучевости и усложненности. Это имеет место, когда в вычислении или внесении параметров не удается учесть значения некоторых факторов, которые могут повлиять на результаты и полученные выводы.
4. Локальность
Математические модели часто строятся на основе данных, полученных в определенном месте, времени и условиях. Поэтому, модели не всегда могут работать при изменении условий, таких как масштаб процесса и его географическое расположение. Следуя таким моделям, можно делать спекулятивные выводы, которые не соответствуют реальности.
5. Влияние человеческого фактора
В работе с математическими моделями может быть незначительное влияние человеческого фактора, например, при выборе модели или параметров. Это может привести к дополнительным ошибкам и искажениям, влияющим на качество и точность результатов.