Что обозначает система в математике

Система в математике — это упорядоченное множество элементов, объединенных определенными правилами или законами. Она может быть использована для решения различных задач и моделирования реальных явлений. Узнайте, что означает система в математике и как она помогает в изучении и понимании математических концепций.

Математика — это наука, которая разрабатывает и изучает различные символы и обозначения, используемые для представления и работы с числами, формулами и уравнениями. Одним из ключевых понятий в математике является понятие системы. Система — это упорядоченный набор символов и правил, которые определяют их использование и взаимодействие. В математике существует несколько различных систем, каждая из которых имеет свои особенности и применение.

Одной из самых распространенных систем в математике является десятичная система. В этой системе используются десять символов — цифры от 0 до 9. Символы комбинируются в различные числа с помощью позиционной нотации, где значение символа зависит от его позиции в числе. Например, число 432 представляет собой сумму 4*100 + 3*10 + 2*1.

Еще одной важной системой является двоичная система. В этой системе используются всего два символа — 0 и 1. Двоичная система широко используется в компьютерной науке и технологиях, так как компьютеры основаны на двоичной логике. В двоичной системе каждая позиция символа в числе имеет вдвое большую степень. Например, число 1010 в двоичной системе означает 1*8 + 0*4 + 1*2 + 0*1 = 10.

Кроме десятичной и двоичной систем, существуют также системы с другими основаниями, такие как шестнадцатеричная система (основание 16) или восьмеричная система (основание 8). В шестнадцатеричной системе используются 16 символов: цифры от 0 до 9 и буквы от A до F, где A = 10, B = 11, и так далее. Восьмеричная система использует 8 символов: цифры от 0 до 7. Эти системы часто используются в программировании и вычислениях с большими числами.

Символы и обозначения также широко используются в математических формулах и уравнениях. Круглые скобки (), квадратные скобки [], фигурные скобки {}, а также различные операторы и знаки служат для группировки и организации математических выражений. Символы +, -, *, / и ^ обозначают базовые математические операции сложения, вычитания, умножения, деления и возведения в степень соответственно.

Понимание и использование символов и обозначений является неотъемлемой частью изучения и практического применения математики. Они позволяют нам представлять, выражать и решать различные математические задачи и проблемы. Поэтому важно освоить базовые системы и научиться правильно интерпретировать и использовать символы и обозначения в математике.

Что обозначает система в математике?

В математике термин «система» обычно относится к набору математических объектов или уравнений, связанных определенными правилами и отношениями. Система может быть использована для описания взаимосвязи между различными элементами или для решения задачи, связанной с этими элементами. В зависимости от контекста, система может быть представлена в виде уравнений, неравенств, матриц, графов или других структур данных.

Системы широко применяются в различных областях математики, физики, экономики, компьютерных наук и других науках, где требуется анализ или решение сложных задач. С их помощью можно описать и изучить различные взаимосвязи и взаимодействия между объектами, а также найти решение для определенной задачи.

В математике системы можно классифицировать по различным признакам, например, по типу уравнений или неравенств, по количеству неизвестных переменных, по свойствам решений и т.д. Некоторые известные примеры систем включают системы линейных уравнений, системы дифференциальных уравнений, системы уравнений с ограничениями и многие другие.

Изучение систем является важной частью математического анализа и может быть полезным инструментом для решения практических задач. Понимание того, как работают системы и как их использовать, позволяет развивать аналитическое мышление и решать сложные задачи эффективно.

Общее понятие системы

Одной из основных черт системы является взаимодействие между ее элементами. Элементы системы могут быть связаны различными отношениями, такими как взаимодействие, влияние или зависимость. Взаимодействие между элементами системы позволяет ей функционировать как единое целое и достигать своих целей.

Системы могут быть физическими или абстрактными. Физические системы существуют в реальном мире и имеют конкретные физические компоненты и свойства. Абстрактные системы, с другой стороны, существуют в мыслях и концепциях и представляют собой упорядоченные наборы идей, правил или символов.

Математические системы используются в математике для формализации и изучения различных математических объектов, таких как числа, функции, геометрические фигуры и другие. Они позволяют математикам анализировать и решать сложные задачи, используя строгую логику и формальные методы.

Обозначение математической системы включает в себя символы, обозначения и правила, которые определяют ее структуру и функции. Символы могут представлять числа, операции, переменные или другие математические объекты. Обозначения и правила описывают, как символы и элементы системы связаны и как функционируют вместе.

В целом, системы играют важную роль в математике, обеспечивая формализацию и структурирование математических понятий и объектов. Они позволяют ученым исследовать и понимать сложные математические структуры и разрабатывать новые методы и теории для решения задач и проблем.

Особенности математической системы

Одной из особенностей математической системы является ее строгость и точность. Все определения, аксиомы и теоремы в математике сформулированы с большой точностью и ясностью. Это позволяет избежать двусмысленности и неоднозначности при работе с математическими объектами.

Еще одной особенностью математической системы является ее формальность. Математика строится на логических законах и принципах, которые позволяют строго доказывать теоремы и выводить новые результаты из уже известных. Формальность математической системы позволяет ей быть надежным инструментом для анализа и решения различных задач.

Также математическая система характеризуется своей универсальностью. Она может быть применена для изучения и описания различных областей знания, таких как физика, экономика, информатика и др. Математика является языком, на котором можно выразить и формализовать множество идей и концепций.

В заключение, математическая система обладает рядом особенностей, которые делают ее уникальным и мощным инструментом для анализа и описания различных явлений. Строгость, формальность и универсальность являются главными чертами математической системы, которые позволяют ей быть эффективным средством для решения задач и получения новых знаний.

Основные символы и обозначения

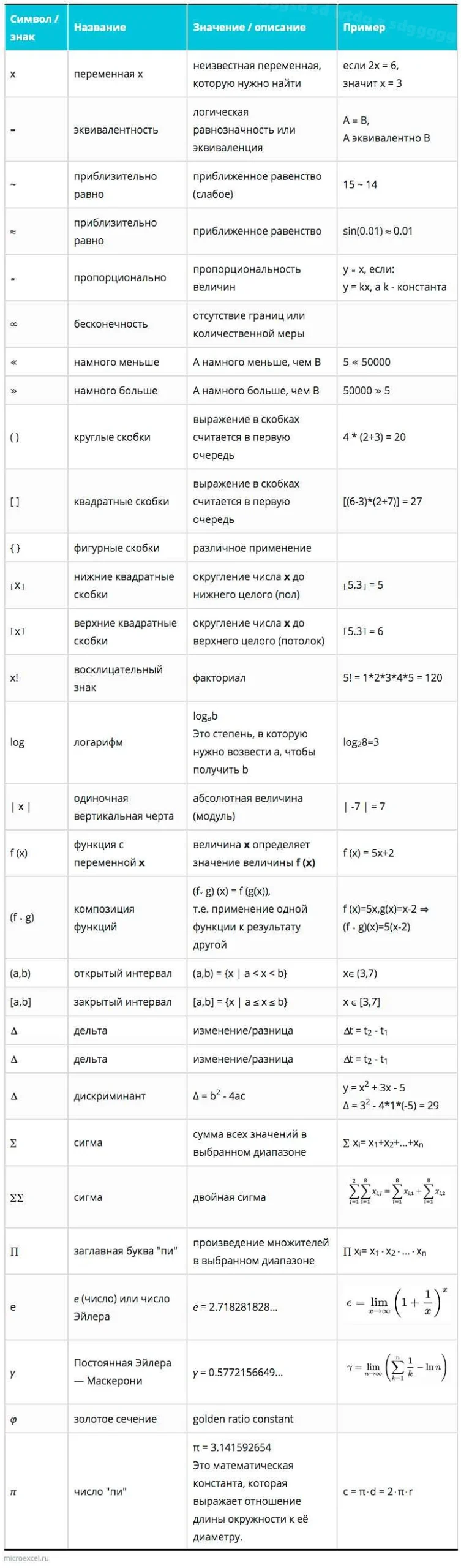
В математике существует множество символов и обозначений, которые используются для представления различных математических объектов, операций и отношений. Некоторые из самых основных символов и обозначений включают:

Числа:

— Целые числа обозначаются символами ℝ (заглавная буква Z). Например, Z = {…, -3, -2, -1, 0, 1, 2, 3, …}.

— Рациональные числа обозначаются символами ℚ (заглавная буква Q). Например, Q = {x | x = p/q, p ∈ Z, q ∈ Z, q ≠ 0}.

— Вещественные числа обозначаются символами ℝ (заглавная буква R).

— Комплексные числа обозначаются символами ℂ (заглавная буква C). Например, C = {a + bi | a, b ∈ R, i^2 = -1}.

Операции:

— Сложение обозначается символом +.

— Вычитание обозначается символом -.

— Умножение обозначается символом · или *.

— Деление обозначается символом ÷ или /.

Отношения:

— Равенство обозначается символом =.

— Неравенство обозначается символами < (меньше), > (больше), ≤ (меньше или равно), ≥ (больше или равно).

— Импликация обозначается символом → (стрелка вправо).

— Эквивалентность обозначается символом ↔ (стрелка влево и вправо).

Множества:

— Множество пустое (без элементов) обозначается символом ∅ (пустое множество).

— Множество всех элементов обозначается символом ∀ (всеобщее множество).

— Включение обозначается символом ∈ (принадлежит к множеству).

— Не включение обозначается символом ∉ (не принадлежит к множеству).

Это лишь небольшой обзор основных символов и обозначений, которые используются в математике. Они играют важную роль в записи и понимании математических выражений и уравнений.

Алфавитные обозначения

В математике часто используются алфавитные обозначения для определения переменных и констант. Это помогает упростить запись и чтение математических формул и уравнений.

Некоторые обозначения относятся к конкретным переменным или константам:

• a, b, c — обозначения для коэффициентов в уравнениях;
• x, y, z — обозначения для переменных;
• n — обозначение для натурального числа;
• i, j, k — обозначения индексов в суммах и произведениях;
• m, n — обозначения для целых чисел;
• p, q — обозначения для простых чисел.

Кроме того, существуют обозначения, которые используются для определения множеств:

• A, B, C — обозначения для множеств;
• U — обозначение для объединения множеств;
• ∩ — обозначение для пересечения множеств;
• ∅ — обозначение для пустого множества.

Алфавитные обозначения позволяют упростить запись математических выражений и сделать их более компактными и понятными. Они являются важным инструментом для математиков и учеников, изучающих математику.

Числовые обозначения

В математике числа обозначаются различными символами и обозначениями. Они используются для обозначения конкретных чисел, наборов чисел, и математических операций.

Наиболее распространенные числовые обозначения включают:

Натуральные числа: обозначаются символом ℕ. Это множество положительных целых чисел, начиная с единицы: 1, 2, 3, 4, и так далее.

Целые числа: обозначаются символом ℤ. Это множество всех положительных и отрицательных целых чисел, включая ноль: …, -3, -2, -1, 0, 1, 2, 3, …

Рациональные числа: обозначаются символом ℚ. Это множество всех чисел, которые можно представить в виде дроби, где числитель и знаменатель являются целыми числами, и знаменатель не равен нулю. Например, 1/2, -3/4, 0.25, и т.д.

Вещественные числа: обозначаются символом ℝ. Это множество всех чисел, которые можно представить на числовой прямой, включая рациональные числа и иррациональные числа, такие как корень из 2 или число π.

Комплексные числа: обозначаются символом ℂ. Это множество чисел, которые могут быть представлены в виде a + bi, где a и b являются вещественными числами, а i — мнимая единица, такая что i² = -1.

Иррациональные числа: обозначаются символом ℑ. Это множество всех чисел, которые не могут быть представлены в виде дроби, таких как корень из 2, число π или е.

Трансцендентные числа: обозначаются символом ℜ. Это множество всех иррациональных чисел, которые не являются алгебраическими числами, то есть не являются корнями полиномов с целыми коэффициентами.

Бесконечность: обозначается символом ∞. Это обозначение для предела, когда число не имеет конца или бесконечно большое.

Это лишь некоторые из числовых обозначений, используемых в математике. Они помогают упростить и стандартизировать запись и понимание математических концепций и операций.

Символы операций

В математике существует множество символов, которые используются для обозначения различных операций. Некоторые из наиболее распространенных символов операций включают:

— Знак плюс (+) используется для обозначения сложения.

— Знак минус (-) используется для обозначения вычитания.

— Знак умножения (×) используется для обозначения умножения.

— Знак деления (÷) используется для обозначения деления.

— Знак равенства (=) используется для обозначения сравнения и установления равенства двух выражений.

— Знак меньше (

— Знак больше (>) используется для обозначения отношения «больше».

— Знак меньше или равно (≤) используется для обозначения отношения «меньше или равно».

— Знак больше или равно (≥) используется для обозначения отношения «больше или равно».

Это лишь некоторые из символов операций, которые используются в математике. Знание этих символов позволяет удобно записывать и читать математические выражения и уравнения.

Пределы и интегралы

Предел функции может быть представлен в виде предела последовательности или предела функции приближающихся к данной точке. Он играет важную роль в анализе и используется для решения различных математических задач.

Интеграл — это математический объект, который обозначает площадь под кривой графика функции в определенном интервале. Он является одним из основных понятий математического анализа и находит широкое применение в физике, экономике, статистике и других областях науки.

Интегралы могут быть определены как неопределенные (интегралы от функций) или определенные (интегралы от функций на заданном интервале). В обоих случаях решение задачи сводится к нахождению антипроизводной функции.

Пределы и интегралы являются важными концепциями в математике и находят широкое применение в различных областях знания.

Системы координат

В математике система координат используется для определения положения точек в пространстве или на плоскости. Она состоит из набора числовых осей и начала координат.

Существует несколько типов систем координат:

• Декартова система координат: оси пересекаются под прямым углом, и точка задается двумя числами — координатами по оси X и по оси Y.
• Полярная система координат: точка задается расстоянием до начала координат и углом, который образует прямая, проведенная из начала координат в эту точку, с положительным направлением.
• Сферическая система координат: точка задается расстоянием до начала координат, углами между осью Z и радиус-вектором, а также углом между радиус-вектором проекции точки на плоскость XY и осью X.

Системы координат широко применяются в различных областях науки и техники, таких как физика, геометрия, графика и другие.

Вопрос-ответ:

Что такое система в математике?

Система в математике — это набор взаимосвязанных элементов или правил, которые используются для решения математических задач. Она может включать в себя как символы и обозначения, так и математические операции и законы.

Какие символы и обозначения часто используются в математике?

В математике используются различные символы и обозначения для обозначения математических объектов и операций. Некоторые из наиболее распространенных символов включают: «+», «-«, «*», «/», «>», »

Какие символы используются для обозначения операций в математике?

Для обозначения различных операций в математике используются следующие символы: «+» для сложения, «-» для вычитания, «*» для умножения, «/» для деления, «^» или «**» для возведения в степень, «√» для извлечения квадратного корня, «!» для факториала и «∑» для суммирования. Кроме того, существуют специальные символы для обозначения математических функций, например, «sin», «cos», «log» и другие.

Какие обозначения используются для обозначения констант и переменных в математике?

В математике обозначения для констант и переменных могут включать буквы латинского и греческого алфавита, а также индексы и верхние индексы. Например, для обозначения переменных часто используются буквы «x», «y», «z» и т.д., а для обозначения констант — буквы «a», «b», «c» и т.д. Для индексов и верхних индексов часто используется нижнее подчеркивание и верхние знаки «^» или «_».

Зачем нужны символы и обозначения в математике?

Символы и обозначения в математике играют важную роль, поскольку они позволяют компактно и точно записывать математические выражения, формулы и уравнения. Они также помогают облегчить понимание и коммуникацию между математиками, так как один и тот же символ может использоваться для обозначения одной и той же математической концепции в разных областях математики.

Что такое система в математике?

Система в математике — это совокупность взаимосвязанных объектов или правил, которые устанавливают порядок и логику в определенной области математики. Она помогает организовать знания и методы решения задач, используя символы и обозначения.

Какие символы и обозначения используются в математике?

В математике используются различные символы и обозначения для представления математических объектов и операций. Некоторые из них включают числа (0, 1, 2, …), арифметические операции (+, -, ×, ÷), знаки сравнения (>,

Видео по теме: