Что обозначает в математике по

В математике термин ‘по’ обозначает отношение или связь между двумя объектами или явлениями. Узнайте, как использовать это понятие в различных областях математики и как оно помогает устанавливать связи и отношения между различными элементами и операциями.

Математика — это наука, изучающая числа, структуры, пространства и изменения. Она имеет свой собственный язык, который включает в себя множество сокращений и обозначений. В этой статье мы рассмотрим некоторые из основных сокращений, используемых в математике, и их значения.

Одним из наиболее распространенных сокращений в математике является символ «пи» — π. Он обозначает отношение длины окружности к ее диаметру. Значение числа «пи» приближенно равно 3.14159. Это число имеет множество интересных свойств и используется во многих формулах и уравнениях.

Еще одним важным сокращением является символ «минус» — −. Он обозначает вычитание одного числа из другого. Например, 5 − 3 равно 2.

Также в математике часто используется символ «дельта» — Δ. Он обозначает разность или изменение. Например, если x и y — два числа, то Δx обозначает разность между ними. Этот символ также используется в теории вероятностей и дифференциальных уравнениях.

Кроме того, необходимо упомянуть символы «пи» и «е» — π и ϵ. Первый обозначает число «пи», а второй — основание натурального логарифма, приближенно равное 2.71828. Они являются одними из наиболее важных констант в математике и широко применяются в различных областях науки и техники.

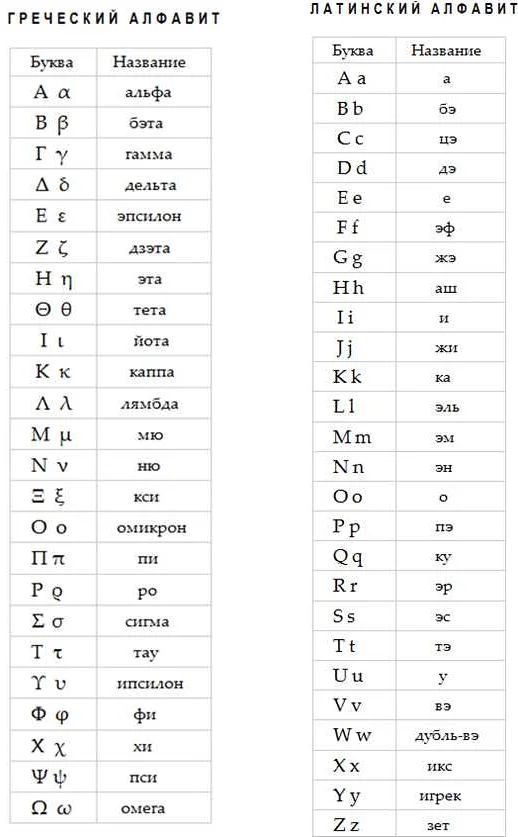
Понятие математики и ее роль в науке

Роль математики в науке трудно переоценить. Она является фундаментальной для многих других наук, таких как физика, химия, экономика и технические науки. Математика предоставляет инструментарий и язык для формулирования и решения проблем в этих областях.

Основная цель математики — это абстрактное моделирование и предсказание реальных явлений и процессов. Она позволяет анализировать данные, находить закономерности, строить модели и проводить прогнозы. Математические методы также используются для оптимизации процессов, принятия решений и разработки новых технологий.

Без математики многие научные и инженерные достижения были бы невозможны. Она играет важную роль в различных областях жизни, от разработки новых лекарств до поиска решений для экологических проблем. Математика также способствует развитию логического мышления, абстрактного мышления и умения решать сложные задачи.

В заключение, математика является фундаментальной наукой, которая играет важную роль в научном и техническом прогрессе. Ее методы и концепции применяются во многих областях жизни и позволяют нам лучше понимать и описывать окружающий нас мир.

Видео по теме:

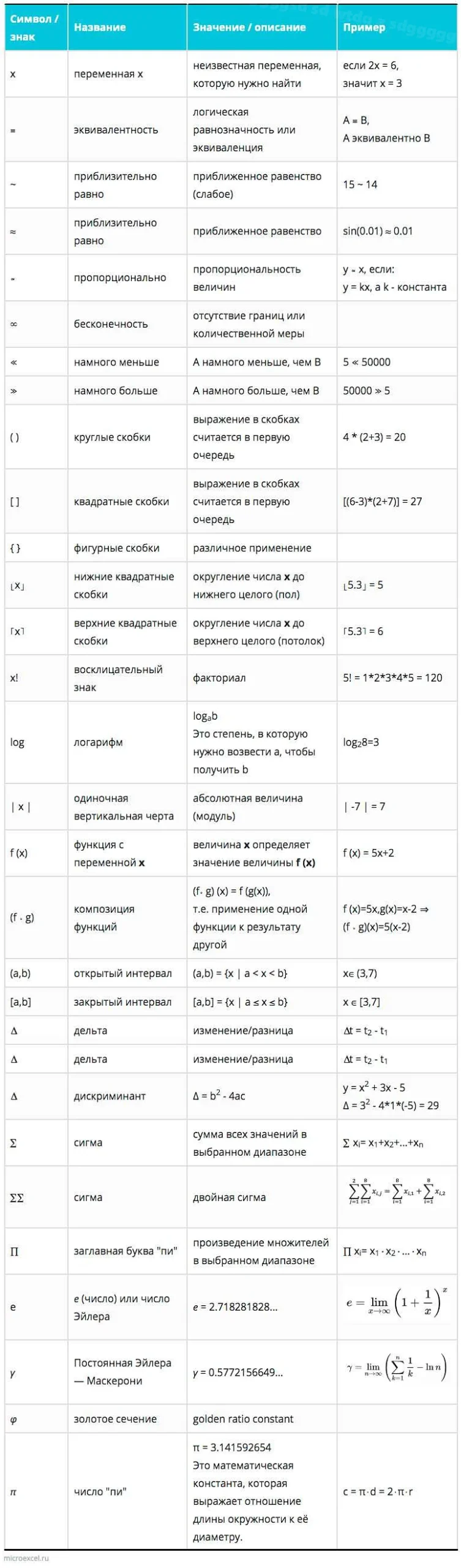
Значение основных сокращений в математике

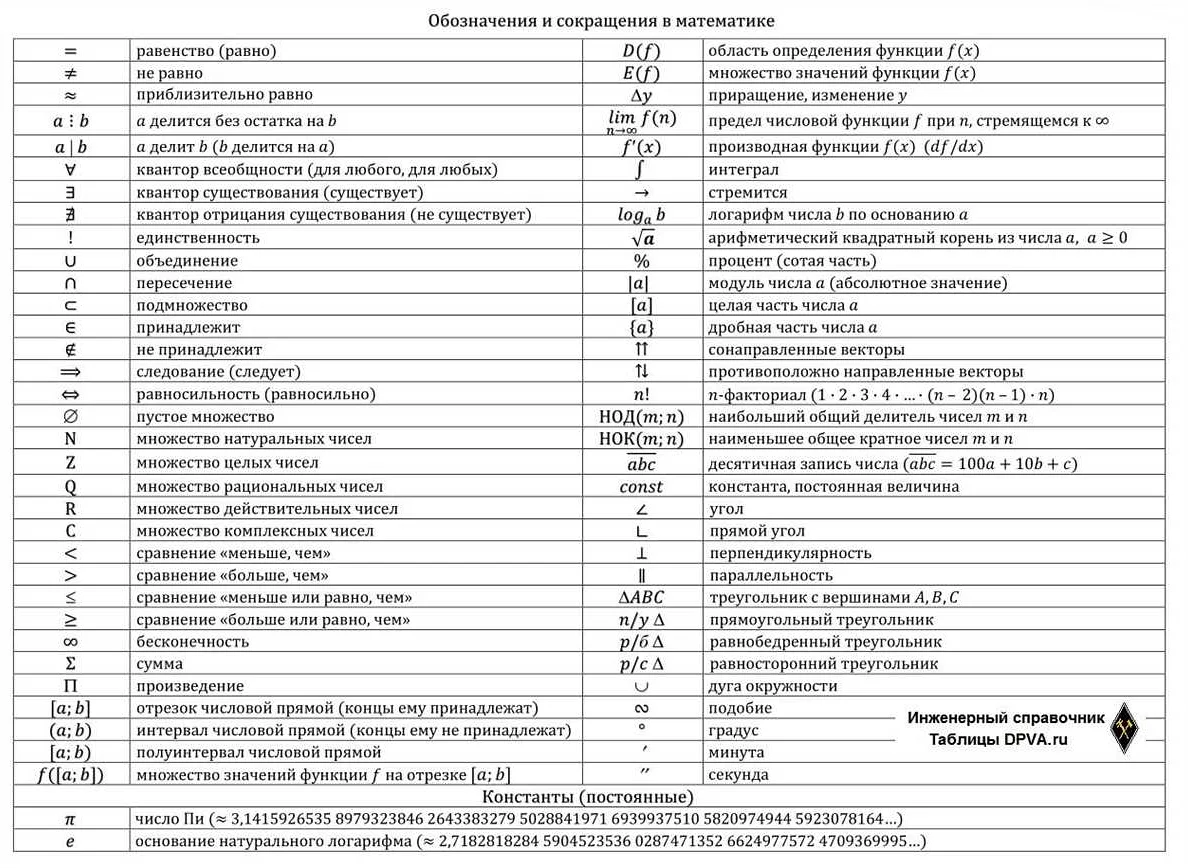
Одним из основных сокращений в математике является знак «=». Этот знак используется для обозначения равенства двух выражений или чисел. Например, «2 + 2 = 4» означает, что сумма двух чисел 2 равна числу 4.

Другим распространенным сокращением является знак «+», который обозначает операцию сложения. Например, «2 + 3» означает, что нужно сложить числа 2 и 3.

Сокращение «-«, знак минуса, используется для обозначения операции вычитания. Например, «5 — 3» означает, что нужно вычесть число 3 из числа 5.

Знак «*», или крестик, обозначает операцию умножения. Например, «2 * 4» означает, что нужно умножить число 2 на число 4.

Знак «/», или косая черта, обозначает операцию деления. Например, «8 / 2» означает, что нужно разделить число 8 на число 2.

Еще одно важное сокращение — «^», или знак степени. Оно используется для обозначения возведения числа в степень. Например, «2^3» означает, что нужно возвести число 2 в куб.

В математике также используются сокращения для обозначения специальных функций, таких как синус (sin), косинус (cos), тангенс (tan), арксинус (asin), арккосинус (acos), арктангенс (atan) и многих других.

Знание основных сокращений и их значений позволяет упростить запись математических выражений и легче понять математические термины и операции.

Определение понятия «Абсолютная величина»

Абсолютная величина числа обозначается символом |x|, где x – число. Она выражает расстояние от числа x до нуля на числовой оси. Независимо от знака числа, его абсолютная величина всегда положительна или равна нулю.

Формально, если x – число, то абсолютная величина |x| определяется следующим образом:

|x| =

 

x,

 

если x ≥ 0,

|x| =

 

-x,

 

если x < 0.

Например, абсолютная величина числа 5 равна 5, а абсолютная величина числа -3 равна 3.

Абсолютная величина широко используется в различных областях математики, физики и других наук. Она позволяет сравнивать и измерять значения без учета их знака и является важным инструментом для решения различных математических задач.

Роль «Бесконечно малой величины» в математике

В математике понятие «бесконечно малой величины» играет важную роль при рассмотрении пределов функций. Бесконечно малая величина обозначается символом ε (эпсилон) и используется для описания изменения функции вблизи определенной точки.

Бесконечно малая величина определяется как такая функция, значение которой стремится к нулю при приближении к заданной точке. Она имеет малую амплитуду, но важна при анализе поведения функции в окрестности этой точки.

В математике существуют различные способы определения бесконечно малых величин. Например, можно использовать понятие предела функции. Функция f(x) считается бесконечно малой при x стремящемся к a, если для любого ε > 0 существует такое δ > 0, что для всех x, удовлетворяющих условию |x — a| < δ, выполняется неравенство |f(x)| < ε.

Бесконечно малые величины широко используются в математическом анализе, дифференциальном исчислении и других областях математики. Они позволяют рассматривать функции в окрестности заданной точки, анализировать их поведение и решать различные задачи, связанные с пределами и производными.

Значение понятия «Логарифм»

Основное свойство логарифма состоит в том, что он позволяет решать уравнения вида a^x = b, находя неизвестное значение x.

Логарифмы широко применяются в различных областях науки и техники. Они позволяют упростить сложные математические выражения и решать различные задачи, связанные с экспоненциальным ростом, процентными изменениями и многими другими.

Основными свойствами логарифма являются:

• Свойство умножения: loga(b * c) = loga(b) + loga(c)
• Свойство деления: loga(b / c) = loga(b) — loga(c)
• Свойство возведения в степень: loga(bc) = c * loga(b)

Логарифмы с широкими применениями в математике включают натуральный логарифм (с основанием e) и десятичный логарифм (с основанием 10).

Знание логарифмов позволяет более эффективно работать с числами и решать сложные задачи в математике и её приложениях.

Определение понятия «Синус»

Синус обозначается символом sin и может принимать значения от -1 до 1. Значение синуса зависит от величины угла, на который опирается треугольник.

Синус является периодической функцией с периодом 2π, что означает, что значения синуса повторяются через каждые 2π радиан.

Синус широко используется в математике, физике и инженерии для решения задач, связанных с волнами, колебаниями и периодическими процессами.

Роль «Косинуса» в математике

Косинус используется в различных областях математики. В геометрии он позволяет вычислять углы между векторами и определять расстояния между точками на плоскости. В аналитической геометрии косинус угла между двумя векторами используется для определения их скалярного произведения.

Кроме того, косинус широко применяется в теории вероятностей и статистике. Он используется для определения корреляции между двумя случайными величинами и для вычисления расстояния между вероятностными распределениями.

В математическом анализе косинус играет важную роль при решении уравнений и дифференциальных уравнений. Также он используется при интегрировании функций и в различных методах численного анализа.

Значение понятия «Тангенс»

Значение тангенса угла можно вычислить с помощью соответствующих тригонометрических таблиц или с помощью калькулятора, на котором есть функция вычисления тангенса.

Тангенс широко применяется в различных областях науки и техники. Он используется, например, в физике для определения углов наклона, в астрономии для определения положения небесных объектов и в инженерии для решения задач, связанных с углами и прямоугольными треугольниками.

Вопрос-ответ:

Что такое «по» в математике?

В математике «по» обозначает отношение или операцию, которая выполняется с помощью определенного правила или алгоритма.

Какие основные сокращения используются в математике?

В математике используются различные сокращения для обозначения разных математических понятий. Некоторые из них включают «нод» (наибольший общий делитель), «нок» (наименьшее общее кратное), «д.б.» (должно быть), «н.у.» (неравенство), и т.д.

Что означает «нод» в математике?

В математике «нод» обозначает наибольший общий делитель двух или более чисел. Например, наибольший общий делитель чисел 12 и 18 равен 6.

Как определить «нок» в математике?

В математике «нок» обозначает наименьшее общее кратное двух или более чисел. Например, наименьшее общее кратное чисел 4 и 6 равно 12.

Когда используется сокращение «д.б.» в математике?

Сокращение «д.б.» в математике используется для обозначения того, что определенное условие должно быть выполнено. Например, в уравнении «x + 5 = 10, д.б. x = 5» означает, что для уравнения x + 5 = 10, значение x должно быть равно 5.

Что означает сокращение «по» в математике?

Сокращение «по» в математике может иметь несколько значений в разных контекстах. Одно из наиболее распространенных значений — это указание на способ выполнения операции или рассмотрения объекта. Например, если говорят «решить уравнение по Лапласу», это означает, что уравнение будет решаться с использованием преобразования Лапласа. В других случаях «по» может обозначать деление или распределение. В общем, значение сокращения «по» в математике зависит от контекста и должно исходить из соответствующих обозначений и правил.