Что такое хорда окружности в математике

Хорда в математике — это отрезок, соединяющий две точки на окружности. Она является одним из основных элементов геометрии окружности и играет важную роль в решении задач на плоскости. Узнайте, какие свойства и формулы связаны с хордой окружности и как она используется в различных областях науки и техники.

Окружность — одна из самых изучаемых и важных геометрических фигур. В математике существует множество понятий и свойств, связанных с окружностью. Одно из таких понятий — хорда окружности.

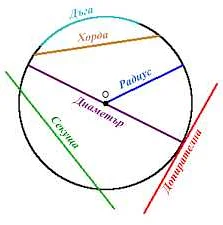
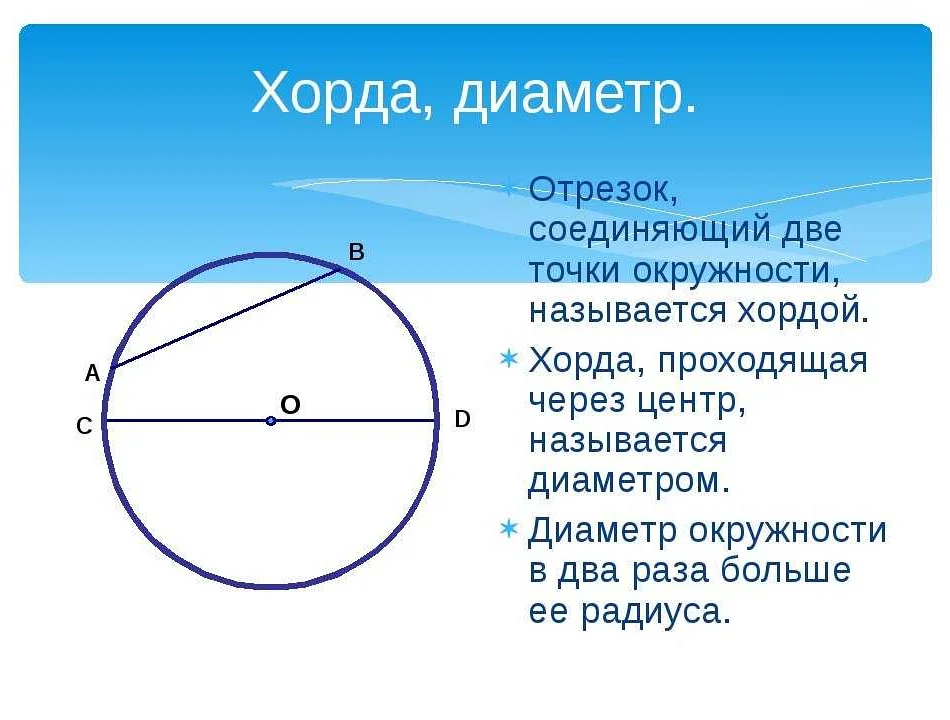
Хордой окружности называется отрезок, соединяющий две точки на окружности. Хорда проходит через центр окружности или нет, важно лишь ее начальная и конечная точки. Длина хорды может быть как меньше, так и больше диаметра окружности.

Хорда является основной составляющей в различных геометрических и алгебраических задачах. Она обладает рядом свойств, которые позволяют использовать ее в решении различных задач. Например, хорда, проходящая через центр окружности, является диаметром и делит окружность на две равные дуги. Дуги, образованные хордой, могут быть как меньше, так и больше полуокружности.

Хорды окружности находят применение не только в математике, но и в различных областях науки и техники. Например, они используются при построении и анализе графиков функций, в проектировании и строительстве, в компьютерной графике и дизайне. Знание свойств и особенностей хорд окружности позволяет более глубоко понять и изучать окружность и ее применение в практических задачах.

Понятие хорды окружности в математике

Основные свойства хорды окружности:

• Диаметр — это частный случай хорды, проходящей через центр окружности. Диаметр является самой длинной хордой окружности.
• Дуга — часть окружности, ограниченная хордой.
• Дуги, ограниченные параллельными хордами, равны между собой.
• Перпендикуляр, опущенный из центра окружности на хорду, делит хорду на две равные части.
• Хорды, равноудаленные от центра окружности, равны между собой.
• Площадь треугольника, образованного хордой и дугой, пропорциональна длине хорды.

Примеры хорды окружности:

1. AB — хорда окружности с конечными точками A и B.
2. CD — диаметр окружности, так как проходит через центр.
3. EF — хорда окружности, не являющаяся диаметром.

Определение хорды окружности

Основная особенность хорды заключается в том, что она всегда лежит внутри окружности и не может быть больше диаметра окружности. Если хорда проходит через центр окружности, она называется диаметром, в противном случае — недиаметром.

Хорды окружности могут быть разной длины, в зависимости от расстояния между точками, которые они соединяют. Если точки находятся близко друг к другу, хорда будет короткой, а если точки находятся далеко друг от друга, хорда будет длинной.

Хорды окружности имеют множество свойств и применений в математике, геометрии и физике. Они являются основой для понятий радиуса, диаметра, центрального угла, дуги и многих других. Изучение хорд окружности позволяет лучше понять геометрические законы и свойства окружностей.

Свойства хорды окружности

Свойства хорды окружности:

1. Хорда равна диаметру окружности, если проходит через ее центр.
2. Хорда меньше диаметра окружности, если находится внутри нее.
3. Хорда больше диаметра окружности, если находится снаружи ее.
4. Через любые две точки на окружности можно провести единственную хорду.
5. Любая хорда, проходящая через центр окружности, является диаметром.
6. Хорда, параллельная диаметру окружности, делит ее на две равные дуги.
7. Хорда, проходящая через центр окружности, делит ее на две равные дуги.
8. Середина хорды является ее точкой пересечения с радиусом, проведенным к центру окружности.
9. Хорда и ее перпендикулярный радиус пересекаются под прямым углом.

Примеры использования свойств хорды окружности могут быть следующими:

• Найти длину хорды, зная радиус и угол, под которым хорда пересекает окружность.
• Доказать, что хорда, проходящая через середину другой хорды, делит ее на две равные части.
• Найти координаты точки пересечения двух хорд на окружности.
• Доказать, что хорда, проходящая через центр окружности, делит ее на две равные дуги.

Примеры хорды окружности

ПримерОписание

Хорда AB	Отрезок, соединяющий точки A и B на окружности.
Хорда CD	Отрезок, соединяющий точки C и D на окружности.
Хорда EF	Отрезок, соединяющий точки E и F на окружности.

Это лишь несколько примеров хорд окружности, их может быть бесконечное множество на любой окружности.

Ссылки на хорду окружности

Если дана хорда окружности и точка, лежащая внутри окружности, то можно провести две хорды, которые пересекают данную точку и делят исходную хорду на три равные части. Это называется теоремой о хордах, которая имеет важное значение в геометрии.

Для более подробного изучения хорды окружности можно обратиться к следующим источникам:

• Математические учебники – в них можно найти определение хорды окружности, ее свойства и примеры задач.
• Геометрические справочники – они содержат подробную информацию о хордах окружности, включая доказательства теорем и различные геометрические примеры.
• Интернет-ресурсы – существуют множество математических сайтов, на которых можно найти информацию о хордах окружности, включая иллюстрации и интерактивные задачи.
• Учебные видео – на платформах для обучения, таких как YouTube или Курсера, можно найти видеоуроки по геометрии, включающие объяснение хорд окружности.

Изучение хорд окружности поможет лучше понять геометрию и ее применение в решении различных задач.

Длина хорды окружности

Формула для вычисления длины хорды окружности имеет вид:

l = 2 * r * sin(α/2)

Где:

• l — длина хорды
• r — радиус окружности
• α — угол, образованный хордой и радиусом

Свойства длины хорды:

• Длина хорды равна диаметру окружности, если хорда является диаметром.
• Длина хорды меньше диаметра окружности.
• Длина хорды увеличивается при увеличении угла, образованного хордой и радиусом.

Примеры вычисления длины хорды:

1. Радиус окружности равен 5, а угол, образованный хордой и радиусом, равен 60 градусов. Тогда:

l = 2 * 5 * sin(60/2) = 2 * 5 * sin(30) = 2 * 5 * 0.5 = 5

Длина хорды равна 5.

2. Радиус окружности равен 7, а угол, образованный хордой и радиусом, равен 120 градусов. Тогда:

l = 2 * 7 * sin(120/2) = 2 * 7 * sin(60) = 2 * 7 * 0.866 = 9.588

Длина хорды равна приблизительно 9.588.

Таким образом, длина хорды окружности зависит от радиуса окружности и угла, образованного хордой и радиусом. Это свойство позволяет расчитывать длину хорды при известных параметрах окружности.

Угол между хордой и радиусом

В геометрии углом между хордой и радиусом называется угол, образованный хордой и радиусом, имеющим общую начальную точку. Этот угол измеряется в радианах или градусах и может быть как положительным, так и отрицательным.

Угол между хордой и радиусом может быть вписанным или центральным. Вписанный угол определяется хордой, которая пересекает окружность, а радиусом, проведенным к точке пересечения. Центральный угол определяется хордой, которая соединяет две точки на окружности, и радиусом, проведенным к центру окружности.

Свойства угла между хордой и радиусом:

• Вписанный угол между хордой и радиусом равен половине угла, стоящего на дуге, охватываемой хордой;
• Центральный угол между хордой и радиусом равен удвоенному вписанному углу;
• Угол между хордой и радиусом определяет длину соответствующей дуги на окружности.

Примеры угла между хордой и радиусом:

• Пусть окружность имеет радиус 5 единиц и хорда, соединяющая две точки на окружности, равна 6 единиц. Угол между хордой и радиусом в данном случае можно найти, используя теорему косинусов;
• Если хорда является диаметром окружности, то угол между хордой и радиусом будет прямым.

Равенство длин хорд, отсекающих равные дуги окружности

Если две хорды окружности отсекают на ней равные дуги, то длины этих хорд также будут равны. Это свойство называется равенством длин хорд, отсекающих равные дуги окружности.

Для доказательства этого свойства рассмотрим окружность с центром O и две хорды AB и CD, которые отсекают равные дуги AC и BD. Предположим, что длина хорды AB меньше длины хорды CD, то есть AB < CD.

Поскольку AC и BD равны, то дуги AC и BD тоже равны. Но по правилу, что дуга, отсекаемая хордой, пропорциональна длине хорды, получаем, что дуга AC должна быть меньше дуги BD.

Таким образом, мы приходим к противоречию, так как утверждение AB < CD противоречит тому, что дуги, отсекаемые хордами, равны. Следовательно, предположение неверно и длины хорд AB и CD равны.

Это свойство может быть использовано для решения различных задач, связанных с окружностями. Например, если известно, что две хорды отсекают равные дуги, то можно сделать вывод о равенстве их длин. И наоборот, если известно, что длины двух хорд равны, то можно утверждать, что они отсекают на окружности равные дуги.

Видео по теме:

Что такое хорда окружности?

Хорда окружности — это отрезок, соединяющий две точки на окружности.

Как можно определить хорду окружности?

Хорду окружности можно определить как отрезок, соединяющий две точки на окружности.

Какие свойства имеет хорда окружности?

Хорда окружности имеет следующие свойства: она всегда меньше диаметра окружности, ее длина равна произведению диаметра на синус половины центрального угла, который она охватывает, и хорда, проведенная через центр окружности, является диаметром.

Можете привести примеры хорды окружности?

Конечно, примеры хорды окружности: отрезок, соединяющий две точки на окружности, например, AB, CD, EF.

Какие приложения имеет понятие хорды окружности в реальной жизни?

Понятие хорды окружности находит применение в различных областях, например, в географии при измерении расстояний между точками на Земле или в архитектуре при построении круглых зданий и сооружений.

Что такое хорда окружности?

Хорда окружности — это отрезок, соединяющий две точки на окружности.