Что означает idem в математике

Idem — это латинское слово, используемое в математике для обозначения того, что что-то является тождественным или одним и тем же. Узнайте, как используется понятие idem в математике и как оно помогает в решении различных задач.

В математике термин «idem» используется для обозначения элемента, который при операции с другими элементами дает тот же результат. Он происходит от латинского слова «idem», что означает «тот же самый». В математической нотации обозначается символом «=», что означает равенство.

Idem является одним из основных понятий в математике и используется в различных областях, таких как алгебра, теория множеств, логика и других. Например, в алгебре idem применяется для определения тождественных элементов или операций, которые сохраняют свойства элементов.

Примером idem является ноль в операции сложения чисел. Если к числу прибавить ноль, то результат будет равен этому числу. Также идентичными элементами являются единица в операции умножения и пустое множество в операции объединения.

Idem играет важную роль в математике и помогает устанавливать связи между элементами и операциями. Умение распознавать и применять idem позволяет упростить вычисления и доказательства в математических задачах.

Происхождение и значение слова «idem»

В математике термин «idem» используется для обозначения элемента, который при операции комбинирования с другим элементом остается неизменным. Например, в алгебре «idem» может означать элемент, который при сложении с другим элементом дает тот же самый элемент.

Примеры использования слова «idem» в математике:

• В полукольце идеалов, элемент, который является идемпотентом, остается неизменным при операции объединения.
• В латинских квадратах, идемпотентные элементы означают элементы, которые не меняют свое значение при операции комбинирования.
• В теории графов, идемпотентные вершины означают вершины, которые остаются неизменными при операции объединения с другими вершинами.

Таким образом, слово «idem» имеет различные значения в разных контекстах, но общая идея заключается в том, что оно обозначает элемент, который остается неизменным при определенной операции или действии.

Определение понятия «idem» в математике

В математике, понятие «idem» используется для обозначения элемента, который при операции умножения образует единичный элемент, то есть элемент, который при умножении на любой другой элемент остается неизменным.

Формально, пусть R — кольцо с единицей, а a — элемент кольца R. Тогда a называется «idem», если выполняется следующее условие:

• a * a = a

То есть, при умножении элемента a на себя получается элемент a.

Примеры элементов, которые являются «idem» в различных кольцах:

• В кольце целых чисел Z нулевой элемент 0 является «idem», так как 0 * 0 = 0.
• В кольце вещественных чисел R и комплексных чисел C единичный элемент 1 является «idem», так как 1 * 1 = 1.
• В кольце булевых значений {0, 1} оба элемента 0 и 1 являются «idem», так как 0 * 0 = 0 и 1 * 1 = 1.

Понятие «idem» имеет важное значение в алгебре и теории кольцевых структур, где исследуются свойства элементов в кольцах и их взаимодействие при операциях.

Примеры использования «idem» в математических уравнениях

Рассмотрим пример с множеством целых чисел. Пусть есть множество A = {1, 2, 3, 4, 5}. Если определить операцию умножения на множестве A, то можно установить, что число 1 является «idem». Это означает, что при умножении числа 1 на любое другое число из множества A, оно будет равно этому числу.

УмножениеРезультат

1 × 1	1
1 × 2	2
1 × 3	3
1 × 4	4
1 × 5	5

Таким образом, число 1 в данном примере является идентичным элементом (idem) при операции умножения.

Это лишь один из возможных примеров использования термина «idem» в математике. В различных областях математики он может иметь разные значения и использоваться для обозначения различных свойств и операций.

Свойства и особенности «idem» в математике

Одним из основных свойств «idem» является сохранение своего значения при повторении. Это означает, что если элемент или операция являются «idem», то при повторении их несколько раз результат остается неизменным.

Примером «idem» может служить операция сложения в арифметике. Если мы складываем число с нулем, то результатом будет само это число. Например, 4 + 0 = 4. В данном случае ноль играет роль «idem», так как его присутствие не меняет значение другого числа.

Другим примером «idem» может служить операция умножения в алгебре. Умножение любого числа на единицу дает в результате само это число. Например, 5 * 1 = 5. В данном случае единица играет роль «idem», так как она не меняет значение другого числа при умножении.

Также стоит отметить, что «idem» может быть не только элементом, но и операцией. Например, операция сложения, при которой складываемый элемент равен результату сложения, является «idem». Это означает, что сложение числа с самим собой дает в результате это число. Например, 3 + 3 = 6.

Таким образом, «idem» в математике обозначает элемент или операцию, обладающую особыми свойствами сохранения значения при повторении. Это понятие широко применяется в различных областях математики, играя важную роль в изучении и анализе различных математических структур и операций.

Связь между «idem» и другими математическими понятиями

Понятие «idem» в математике тесно связано с другими важными понятиями и операциями. Оно используется для обозначения элемента, который обладает свойством «идентичности» или «тождественности».

В частности, понятие «idem» тесно связано с понятием «единичного элемента» или «нейтрального элемента» в алгебре. Одним из основных свойств idem является то, что при операции умножения (в алгебре) или композиции (в теории категорий) с ней, другие элементы не изменяются. Таким образом, idem является идентичным элементом для всей группы элементов, с которыми он взаимодействует.

Также понятие «idem» имеет отношение к понятию «проекции» в линейной алгебре. Вектор, который сохраняется при действии линейного оператора, называется idem-вектором или проекцией. Проекции используются для описания различных явлений в физике и геометрии, а также для решения систем уравнений.

Кроме того, в теории категорий понятие «idem» связано с понятием «ретрактов». Ретракт — это такая часть объекта, которая является idem-объектом. То есть, ретракт является подобъектом, который является идентичным объектом для изначального объекта.

Итак, понятие «idem» имеет глубокую связь с другими понятиями и операциями в математике. Оно помогает описывать и анализировать различные структуры и отношения между элементами в различных областях математики.

Применение «idem» в различных областях математики

Термин «idem» имеет широкое применение в различных областях математики. Ниже приведены несколько примеров его использования:

1. В алгебре. В алгебре термин «idem» используется для обозначения элемента множества, который является идемпотентным относительно заданной операции. Идемпотентный элемент удовлетворяет условию, что повторное применение операции к нему не изменяет его значение. Например, в множестве {0, 1} с операцией сложения идемпотентным элементом является 0, так как 0 + 0 = 0.
2. В теории графов. В теории графов «idem» может использоваться для обозначения вершины графа, которая является идемпотентной относительно заданной операции. Идемпотентная вершина обладает свойством, что повторное применение операции к ней не меняет ее состояние. Например, в графе, представляющем сеть передачи данных, идемпотентной вершиной может быть узел, через который данные могут быть переданы в любом количестве, но его состояние не изменится.
3. В теории категорий. В теории категорий термин «idem» может использоваться для обозначения морфизма, который является идемпотентным относительно композиции морфизмов. Идемпотентный морфизм обладает свойством, что повторное применение композиции к нему не изменяет его результат. Например, в категории множеств и функций идемпотентным морфизмом может быть функция, которая возвращает тождественное отображение на множестве.

Это лишь несколько примеров применения термина «idem» в математике. Термин может иметь более специфическое значение в каждой отдельной области и использоваться для обозначения различных концепций и свойств.

Значимость «idem» в научных исследованиях и приложениях

Одним из примеров использования «idem» является его применение в алгебре и теории групп. В этом контексте «idem» обозначает элемент, который, когда умножается на себя, остается неизменным. Такой элемент также называется идемпотентом. В теории групп «idem» используется для описания свойств групповых операций и их элементов.

В физике «idem» может использоваться для описания повторяющихся процессов или состояний. Например, в квантовой механике «idem» может обозначать оператор, который приводит систему в то же состояние, в котором она находилась до применения оператора.

В компьютерных науках «idem» может использоваться для описания операций, которые не меняют состояние объекта или системы. Например, в базах данных «idem» может обозначать операцию, которая не имеет эффекта на данные или их структуру.

В целом, «idem» играет важную роль в научных исследованиях и приложениях, позволяя описывать и анализировать различные аспекты математических, физических и компьютерных систем.

Вопрос-ответ:

Что означает idem в математике?

Idem в математике — это латинское слово, которое означает «то же самое». В математике оно используется для обозначения равенства или эквивалентности двух выражений или объектов. Если два выражения или объекта считаются idem, это означает, что они идентичны или эквивалентны друг другу и могут быть заменены одно на другое без изменения результата.

Как можно использовать понятие idem в математике?

Понятие idem в математике можно использовать в различных областях. Например, в алгебре idem используется для определения равенства между элементами в полугруппах или кольцах. В логике idem может использоваться для определения эквивалентности логических выражений. В общем смысле, idem можно использовать в любой математической области, где необходимо сравнение или замена выражений или объектов.

Можете привести примеры понятия idem в математике?

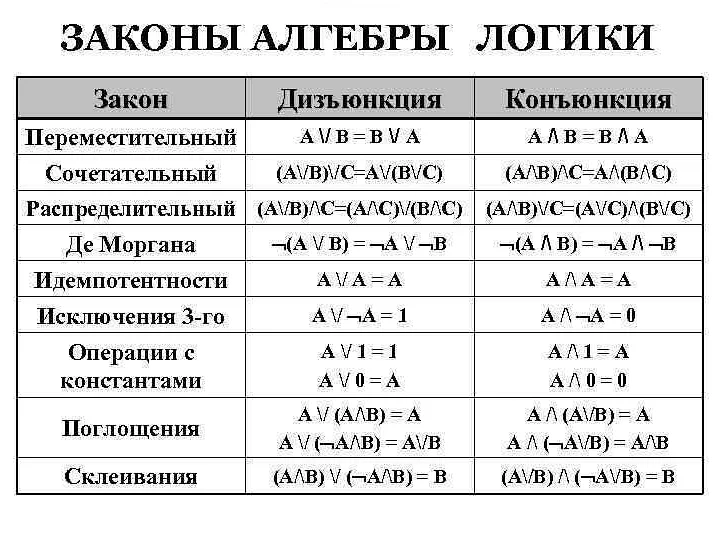
Конечно! В алгебре одним из примеров idem является равенство коммутативного закона сложения: a + b = b + a, где a и b — любые числа. Это означает, что порядок слагаемых не влияет на результат сложения. В логике другим примером idem является эквивалентность двух логических выражений: p ∨ q = q ∨ p, где p и q — любые логические выражения. Это означает, что порядок дизъюнкции не влияет на истинность выражения.

Как понятие idem связано с другими математическими понятиями?

Понятие idem в математике связано с понятиями равенства и эквивалентности. Равенство означает полное совпадение двух выражений или объектов, в то время как эквивалентность означает, что два выражения или объекта могут быть заменены друг на друга без изменения результата. Idem является более общим понятием, которое может быть использовано как для равенства, так и для эквивалентности.

Какое значение имеет понятие idem в математике?

В математике понятие idem имеет значение равенства или эквивалентности двух выражений или объектов. Оно позволяет сравнивать и заменять выражения или объекты, основываясь на их идентичности или эквивалентности. Понятие idem помогает упростить математические выкладки и выводы, облегчая работу с различными выражениями и объектами.

Выводы о роли «idem» в математике и его практическом применении

В математике термин «idem» используется для обозначения элемента, который при операции умножения обладает свойством идемпотентности. Это означает, что при повторном применении операции к этому элементу результат не изменяется.

Роль «idem» в математике заключается в том, что он позволяет упростить вычисления и анализ различных алгебраических структур. Например, в теории групп элемент «idem» может служить идентификатором для нахождения подгрупп с определенными свойствами. В теории кольцевых и алгебраических структур «idem» позволяет классифицировать элементы и определять различные свойства их комбинаций.

Практическое применение концепции «idem» можно найти в различных областях науки и техники. Например, в компьютерных науках «idem» может использоваться для оптимизации алгоритмов и структур данных, учитывая свойства идемпотентности операций. В теории управления «idem» может служить для моделирования и анализа систем с повторяющимися процессами или действиями.

Таким образом, понимание роли «idem» в математике и его практического применения позволяет использовать этот концепт для упрощения вычислений, классификации элементов и оптимизации различных алгоритмов и систем.

Видео по теме: