Что означает перечеркнутая z в математике
Содержимое
- 1 Что означает перечеркнутая z в математике
- 1.1 Что означает перечеркнутая z в математике?
- 1.2 Видео по теме:
- 1.3 Определение и значение символа z с перечерком
- 1.4 Применение и использование перечеркнутой буквы z
- 1.5 Вопрос-ответ:
- 1.5.0.1 Для чего используется перечеркнутая z в математике?
- 1.5.0.2 Как читать перечеркнутую z в математике?
- 1.5.0.3 Какие другие символы используются для обозначения множества всех целых чисел?
- 1.5.0.4 Какие примеры использования перечеркнутой z в математике?
- 1.5.0.5 Какая связь между перечеркнутой z и множеством всех целых чисел?
- 1.6 Примеры использования перечеркнутой z в математике
- 1.7 Значение перечеркнутой буквы z в уравнениях и системах
- 1.8 Перечеркнутая z в комплексных числах: объяснение и свойства
- 1.9 Перечеркнутая z в теории вероятности и статистике
- 1.10 Интересные факты и особенности перечеркнутой z в математике
Перечеркнутая z в математике обозначает комплексно-сопряженное число. Узнайте, как использовать перечеркнутую z и как она связана с другими математическими понятиями.
В математике перечеркнутая z обозначает комплексно сопряженное число z-черта. Комплексно сопряженное число получается путем изменения знака мнимой части исходного числа. Если z = a + bi, где a и b — вещественные числа, то z-черта = a — bi. Таким образом, перечеркнутая z указывает на число, которое симметрично относительно вещественной оси.
Перечеркнутая z часто используется при решении задач, связанных с комплексными числами. Например, при нахождении корней уравнений или при вычислении суммы и разности комплексных чисел. Комплексно сопряженные числа также играют важную роль в физике, инженерии и других областях, где требуется работа с векторами и сигналами.
Заметим, что если z является действительным числом, то его перечеркнутая форма равна исходному числу (z = z-черта). Это свойство особенно полезно при работе с вещественными числами, так как позволяет упростить вычисления и алгебраические преобразования.
Использование перечеркнутой z в математике помогает упростить запись и анализ комплексных чисел и их свойств. Она также предоставляет удобный способ обозначить комплексно сопряженное число и использовать его в дальнейших вычислениях. Понимание значения перечеркнутой z позволяет более глубоко изучить комплексную алгебру и применять ее в решении различных математических и физических задач.
Что означает перечеркнутая z в математике?
Комплексное сопряжение числа используется в различных областях математики, включая анализ, геометрию и теорию чисел. Одно из применений комплексного сопряжения — нахождение модуля комплексного числа. Модуль комплексного числа z определяется как |z| = √(a^2 + b^2).
Также, комплексное сопряжение позволяет находить сопряженные корни многочленов с комплексными коэффициентами и использовать их в решении уравнений.
Например, если z = 2 + 3i, то перечеркнутая z будет равна z̅ = 2 — 3i.
Видео по теме:
Определение и значение символа z с перечерком

Математически, если z = a + bi, где a и b — действительные числа, то z̅ = a — bi. Другими словами, если у нас есть комплексное число вида a + bi, где a — действительная часть, а bi — мнимая часть, то комплексно сопряженное число будет иметь вид a — bi.
Перечеркнутый символ z часто используется в математических выражениях и уравнениях, где требуется нахождение комплексно сопряженного числа. Например, при решении задач, связанных с комплексными числами, перечеркнутый символ z позволяет нам найти сопряженное число, которое может быть полезно для дальнейших вычислений.
Определение и значение символа z с перечерком являются важными концепциями в комплексном анализе и математике в целом. Понимание и использование этого символа помогает математикам и исследователям более эффективно работать с комплексными числами и их свойствами.
Применение и использование перечеркнутой буквы z
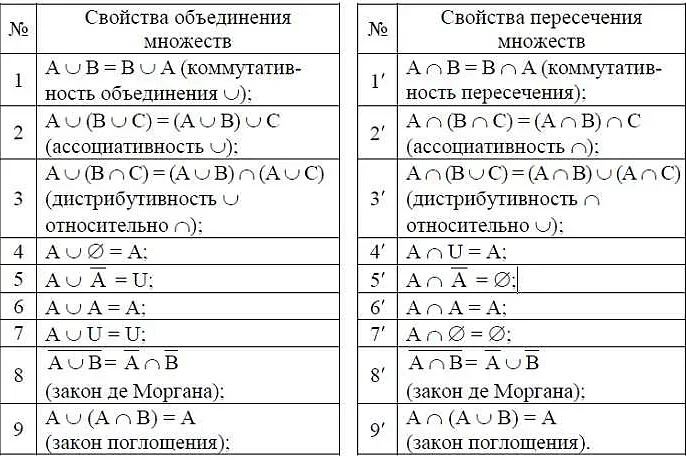
Перечеркнутая буква z (z̶) в математике используется для обозначения действия «зачеркивания» или «отрицания» элемента. Эта нотация позволяет выразить отрицание или исключение конкретного элемента из множества.
Пример использования перечеркнутой буквы z:
Пусть дано множество A = {1, 2, 3, 4, 5}, и множество B = {3, 4, 5}. Тогда множество A\B (читается как «A без B») обозначает множество элементов из A, которые не принадлежат множеству B. Математически это записывается как:
A\B = {1, 2}.
В данном примере элементы 3, 4 и 5, принадлежащие множеству B, исключаются из множества A с помощью перечеркнутой буквы z, чтобы получить новое множество A\B, состоящее только из элементов 1 и 2.
Также перечеркнутая буква z может использоваться для обозначения отрицания какой-либо утверждения, например:
Если утверждение P истинно, то перечеркнутая буква z над P обозначает отрицание этого утверждения ~P.
Использование перечеркнутой буквы z в математике позволяет удобно и ясно выразить отрицание элемента или утверждения и обозначить результат операции исключения из множества.
Вопрос-ответ:
Для чего используется перечеркнутая z в математике?
Перечеркнутая z в математике обозначает множество всех целых чисел. Она используется для обозначения этого множества в некоторых математических областях, например в теории чисел. Множество всех целых чисел обозначается символом Z.
Как читать перечеркнутую z в математике?
Перечеркнутая z в математике читается как «зэта-перечеркнутое» или «зэта-перечеркнутая». Этот символ обозначает множество всех целых чисел.
Какие другие символы используются для обозначения множества всех целых чисел?
Помимо перечеркнутой z, множество всех целых чисел может быть обозначено символом Z с двойной чертой сверху или без перечеркнутой z. В разных областях математики могут использоваться различные обозначения, но все они указывают на одно и то же множество всех целых чисел.
Какие примеры использования перечеркнутой z в математике?
Перечеркнутая z в математике используется во множественных примерах, например, множество всех целых чисел можно записать как Z = {…, -3, -2, -1, 0, 1, 2, 3, …}. Это множество содержит положительные и отрицательные целые числа, а также ноль.
Какая связь между перечеркнутой z и множеством всех целых чисел?
Перечеркнутая z в математике является символом, обозначающим множество всех целых чисел. Это означает, что перечеркнутая z и множество всех целых чисел тесно связаны между собой — каждый раз, когда вы видите символ перечеркнутой z, вы знаете, что он обозначает множество всех целых чисел.
Примеры использования перечеркнутой z в математике
Перечеркнутая z в математике обозначает совокупность множества чисел, которые удовлетворяют определенным условиям.
Например, символ z̶ может использоваться для обозначения перечеркнутого комплексного числа. Комплексные числа представляют собой совокупность чисел вида a + bi, где a и b — действительные числа, а i — мнимая единица, такая что i^2 = -1.
Если мы имеем комплексное число z = 2 + 3i, то его перечеркнутый вариант будет обозначаться как z̶ = 2 — 3i. Таким образом, перечеркнутая z указывает на комплексно-сопряженное число.
В другом примере, перечеркнутая z может использоваться для обозначения перечеркнутой переменной или неизвестной величины. Например, если у нас есть уравнение x + y = 5, и мы хотим найти значение y при известном значении x, мы можем обозначить перечеркнутую переменную z = y — x. Тогда наше уравнение станет z + x = 5, и мы сможем решить его для z.
Вывод: перечеркнутая z в математике может быть использована для обозначения перечеркнутого комплексного числа или перечеркнутой переменной, в зависимости от контекста.
Значение перечеркнутой буквы z в уравнениях и системах

Например, в уравнении 2x + 3y = z, переменная z может принимать любое значение в зависимости от значений переменных x и y. Это может быть полезно, когда требуется найти все решения уравнения при различных значениях x и y.
Перечеркнутая буква z также может использоваться для обозначения параметра в системах уравнений. В таких случаях уравнение соответствует некоторому условию или ограничению, а перечеркнутая переменная указывает на параметр, который может изменяться в пределах указанных ограничений.
Например, в системе уравнений:
2x + 3y = z
x + y = 5
переменная z является параметром, который может изменяться в зависимости от значений переменных x и y, удовлетворяющих второму уравнению.
Таким образом, перечеркнутая буква z в уравнениях и системах уравнений обычно обозначает переменную, которая может быть свободной или параметром, который может изменяться в пределах указанных ограничений.
Перечеркнутая z в комплексных числах: объяснение и свойства
Перечеркнутая z обозначает сопряженное комплексное число. Сопряженное комплексное число z̅ получается из исходного числа z путем изменения знака мнимой части. Если z = a + bi, то z̅ = a — bi. То есть, если исходное число имеет положительную мнимую часть, то сопряженное число будет иметь отрицательную мнимую часть, и наоборот.
Свойства перечеркнутой z в комплексных числах:
- Если z = a + bi, то z̅ = a — bi
- z + z̅ = 2a (мнимые части при сложении взаимно уничтожаются)
- z — z̅ = 2bi (вещественные части при вычитании взаимно уничтожаются)
- z * z̅ = a^2 + b^2 (произведение комплексного числа и его сопряженного равно квадрату модуля исходного числа)
Использование перечеркнутой z в комплексных числах позволяет упростить вычисления и анализ комплексных функций. Она помогает найти сопряженное число, а также определить модуль и аргумент комплексного числа.
Перечеркнутая z в теории вероятности и статистике

Перечеркнутая z (з) в теории вероятности и статистике обычно обозначает стандартное нормальное распределение. Это распределение имеет среднее значение 0 и стандартное отклонение 1.
Стандартное нормальное распределение играет важную роль в статистике и вероятности, так как позволяет проводить различные статистические тесты и оценивать вероятности событий.
Когда переменная имеет стандартное нормальное распределение, ее значения можно преобразовать с помощью таблицы стандартного нормального распределения. Эта таблица позволяет определить вероятность попадания значений переменной в определенный интервал.
Например, если имеется стандартное нормальное распределение, и мы хотим узнать вероятность того, что значение переменной будет меньше или равно определенному значению, мы можем использовать таблицу стандартного нормального распределения для определения этой вероятности.
Значение zВероятность
| -1.96 | 0.025 |
| 0 | 0.5 |
| 1.96 | 0.975 |
В таблице приведены значения z (стандартных отклонений) и соответствующие вероятности. Например, вероятность попадания значения переменной в интервал от -1.96 до 1.96 равна 0.95 (0.025 + 0.5 + 0.975).
Таким образом, перечеркнутая z в теории вероятности и статистике обозначает стандартное нормальное распределение, которое позволяет проводить различные статистические тесты и оценивать вероятности событий.
Интересные факты и особенности перечеркнутой z в математике
Важно отметить, что при работе с комплексными числами, их комплексно сопряженные значения играют важную роль. Например, комплексное число, умноженное на свое комплексно сопряженное значение, всегда будет вещественным числом. Это свойство используется в решении многих задач и проблем в физике, инженерии, и других областях науки.
Интересно отметить, что символ перечеркнутой z занимает особое место в комплексном анализе и теории функций. Он используется для обозначения глобальных комплексных переменных или функций, как например в теории Римана поверхностей.
Комплексные числа и комплексные функции играют важную роль в математике и ее приложениях. Перечеркнутая z представляет собой одну из ключевых концепций в работе с комплексными числами и функциями, и ее использование может привести к интересным и полезным результатам.



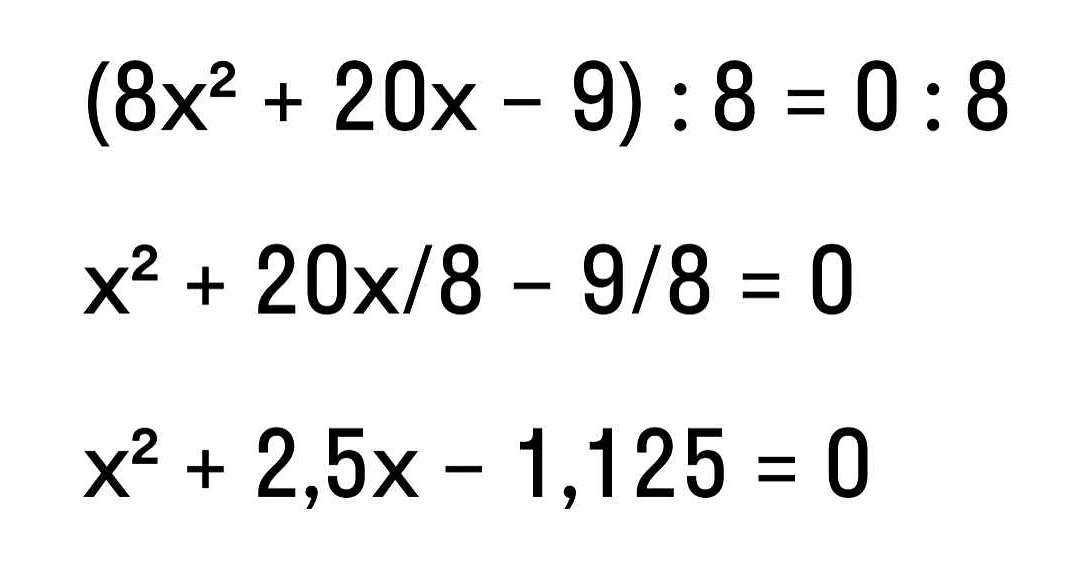

Перечеркнутая z в математике обозначает комплексно-сопряженное число. Это означает, что если у нас есть число z = a + bi, где a и b — вещественные числа, то перечеркнутая z будет обозначаться как z̅ = a — bi. Таким образом, перечеркнутая z является результатом замены знака перед мнимой частью числа. Перечеркнутая z находит широкое применение в алгебре и анализе, особенно при решении уравнений и задач, связанных с комплексными числами. Она используется для определения сопряженного числа, которое имеет такие же вещественные части, но противоположные мнимые части. Пример использования перечеркнутой z может быть следующим: пусть у нас есть число z = 2 + 3i. Тогда его комплексно-сопряженное число будет z̅ = 2 — 3i. Это означает, что вещественная часть остается неизменной, а мнимая часть меняет знак. Перечеркнутая z играет важную роль в математике, и ее понимание позволяет более глубоко разобраться в комплексных числах и их свойствах.
Математика всегда вызывала у меня интерес, поэтому я с удовольствием прочитал эту статью. Что же означает перечеркнутая z в математике? Как оказалось, эта символика используется для обозначения комплексно сопряженного числа. Комплексно сопряженное число получается путем изменения знака мнимой части числа. Например, если у нас есть число z = 3 + 2i, то его комплексно сопряженное число будет обозначаться как z̄ = 3 — 2i. Перечеркнутая z имеет несколько интересных свойств. Во-первых, если мы возьмем комплексно сопряженное от комплексно сопряженного числа, то получим исходное число: z̄̄ = z. Во-вторых, если у нас есть два числа z и w, то комплексно сопряженное от суммы этих чисел будет равно сумме комплексно сопряженных чисел: (z + w̄) = z̄ + w̄. Это свойство можно расширить и на произведение двух чисел: (zw̄) = z̄w̄. Перечеркнутая z является важным инструментом в комплексном анализе и находит применение во многих областях математики и физики. Зная ее свойства, мы можем решать различные задачи, например, находить корни уравнений или решать системы линейных уравнений. В целом, статья помогла мне лучше понять, что означает перечеркнутая z в математике. Теперь я могу применять ее знания в практике и расширять свои знания в области математики.
Перечеркнутая z в математике означает комплексно сопряженное число. Когда мы перечеркиваем букву z, это означает, что мы рассматриваем число, которое симметрично относительно вещественной оси на комплексной плоскости. Например, если у нас есть комплексное число z = a + bi, где a и b — вещественные числа, то перечеркнутая z будет иметь вид z = a — bi. Это понятие полезно во многих областях математики, физики и инженерии. Например, комплексно сопряженные числа используются для нахождения корней многочлена, решения систем линейных уравнений и анализа колебаний в электрических цепях. Они также играют важную роль в теории вероятностей и статистике. Таким образом, перечеркнутая z в математике помогает нам работать с комплексными числами и использовать их в различных приложениях. Это важное понятие, с которым полезно быть знакомым, особенно если вы изучаете математику или связанные с ней дисциплины.