Что в математике означает i

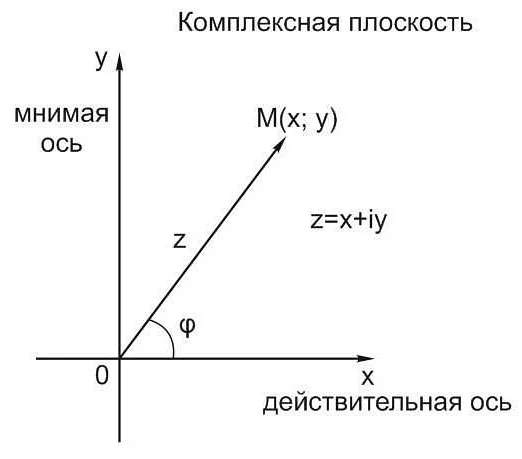
i в математике означает мнимую единицу, которая определяется как квадратный корень из -1. Мнимое число i используется для работы с комплексными числами и имеет ряд уникальных свойств и приложений в различных областях математики и физики.

i — это мнимая единица в математике, которая имеет особое значение и широко используется в комплексном анализе и других областях. Она определяется как квадратный корень из -1: i^2 = -1. Введение этой мнимой единицы позволяет решать уравнения, которые иначе были бы неразрешимыми.

Использование i в математике позволяет работать с комплексными числами, которые представляют собой комбинацию действительной и мнимой части. Комплексные числа записываются в виде a + bi, где a — действительная часть, b — мнимая часть, а i — мнимая единица.

Комплексные числа играют важную роль в математике и находят применение в различных областях, таких как физика, инженерия и информатика. Благодаря мнимой единице i мы можем решать уравнения, моделировать электрические цепи, анализировать колебания и многое другое.

Что такое значение i в математике?

Значение i определяется как корень из -1: i = √(-1). Оно имеет особые свойства и используется для обозначения комплексных чисел, которые представляются в виде суммы действительной и мнимой частей.

Комплексные числа записываются в виде a + bi, где a — действительная часть, а b — мнимая часть. Например, число 3 + 4i является комплексным числом, где действительная часть равна 3, а мнимая часть равна 4.

Значение i широко используется в различных областях математики, физики и инженерии для решения сложных задач. Оно помогает описывать и анализировать такие явления, как электрические цепи, колебательные процессы, квантовая механика и другие.

Роль символа i в математических выражениях

Символ i, известный также как мнимая единица, играет важную роль в математических выражениях, особенно в области комплексного анализа. Он представляет собой квадратный корень из -1, то есть число, для которого выполняется равенство i^2 = -1.

Символ i используется для обозначения мнимой части комплексного числа. Комплексное число представляет собой комбинацию действительной и мнимой частей, например, a + bi, где a и b — действительные числа, а i — символ мнимой единицы. Мнимая часть позволяет представлять числа, которые не могут быть представлены на вещественной оси числовой прямой.

Символ i также широко используется в комплексном анализе, который изучает функции, определенные на комплексной плоскости. Комплексный анализ имеет множество приложений в различных областях, таких как физика, инженерия и теория вероятностей.

Символ i обладает несколькими свойствами, которые позволяют его использовать в различных математических операциях. Например, умножение числа на i приводит к повороту числа на 90 градусов вокруг начала координат в комплексной плоскости. Также существует формула Эйлера, которая связывает символ i с другими математическими константами, такими как число e и гармонические функции.

Использование символа i в математических выражениях позволяет решать широкий спектр задач, включая электротехнику, теорию сигналов, квантовую механику и многое другое. Понимание роли символа i и его свойств позволяет математикам и инженерам решать сложные задачи и разрабатывать новые теории и методы.

Применение значения i в алгебре

Значение i в математике, также известное как мнимая единица, имеет важное применение в алгебре. Оно используется для обозначения мнимых чисел, которые не могут быть представлены на числовой оси. Мнимые числа включают в себя квадратный корень из отрицательного числа, такого как √(-1).

Использование значения i позволяет ввести новые математические объекты, такие как комплексные числа. Комплексное число представляет собой комбинацию вещественной и мнимой частей, записываемых в виде a + bi, где a — вещественная часть, а b — мнимая часть, умноженная на i.

Значение i также используется для определения операций с комплексными числами, таких как сложение, вычитание, умножение и деление. Например, умножение комплексных чисел выполняется путем перемножения их вещественных и мнимых частей, а также использования свойств мнимой единицы, таких как i^2 = -1.

Применение значения i в алгебре позволяет решать сложные математические проблемы, которые не могут быть решены с помощью обычных вещественных чисел. Оно также находит свое применение в физике, инженерии и других науках, где комплексные числа используются для моделирования и анализа различных явлений.

Таким образом, значение i играет важную роль в алгебре, позволяя работать с мнимыми числами и комплексными числами. Это открывает новые возможности для решения математических задач и развития научных и технических дисциплин.

Использование комплексных чисел с i

Математическое обозначение i используется для обозначения мнимой единицы или комплексного числа, которое определяется как квадратный корень из -1.

Комплексные числа с i имеют следующий вид: a + bi, где a и b являются действительными числами, а i — мнимая единица.

Использование комплексных чисел с i широко распространено в различных областях математики и физики. Например, комплексные числа с i используются в решении уравнений, моделировании электрических цепей и в комплексном анализе.

Комплексные числа с i также позволяют представить точки на плоскости, где действительная часть числа соответствует координате по оси x, а мнимая часть числа соответствует координате по оси y.

Использование комплексных чисел с i облегчает решение сложных математических задач и позволяет работать с числами, которые не являются действительными. Это делает их мощным инструментом для анализа и моделирования различных явлений и процессов.

Важно отметить, что комплексные числа с i также имеют свои особенности и правила работы, которые следует учитывать при их использовании. Например, умножение двух комплексных чисел с i осуществляется по правилу распределения и свойству i^2 = -1.

В заключение, использование комплексных чисел с i позволяет расширить возможности математического анализа и решения задач, предоставляя инструменты для работы с числами, которые не являются действительными. Это важное понятие в математике, которое находит применение в различных областях науки и техники.

Значение i в тригонометрии

Тригонометрические функции, такие как синус, косинус и тангенс, могут быть определены как экспоненциальные функции, включающие мнимую единицу i. Например, синус и косинус могут быть выражены через экспоненциальную функцию с использованием формулы Эйлера:

ФункцияФормула

Синус	sin(x) = (eix — e-ix) / (2i)
Косинус	cos(x) = (eix + e-ix) / 2

Где x — угол, e — основание натурального логарифма. Использование мнимой единицы i позволяет связать тригонометрические функции с комплексными числами и решать различные задачи в тригонометрии и алгебре.

Таким образом, значение i в тригонометрии играет важную роль при определении и вычислении тригонометрических функций и связывает их с комплексными числами.

Использование i в формулах тригонометрических функций

В математике символ i используется для обозначения мнимой единицы. Мнимая единица определяется как число, квадрат которого равен -1. Использование i позволяет расширить множество действительных чисел и включить в него комплексные числа.

В тригонометрии символ i используется для представления комплексных чисел в показательной форме. Комплексное число в показательной форме может быть записано как r * (cos(θ) + i * sin(θ)), где r — модуль комплексного числа, θ — аргумент комплексного числа.

Тригонометрические функции, такие как синус, косинус и тангенс, также могут быть выражены с использованием i. Например, синус и косинус комплексного аргумента θ могут быть записаны следующим образом:

ФункцияЗапись с использованием iЗапись без использования i

Синус	sin(θ) = (eiθ — e—iθ) / (2i)	sin(θ) = (eiθ — e—iθ) / 2
Косинус	cos(θ) = (eiθ + e—iθ) / 2	cos(θ) = (eiθ + e—iθ) / 2

Таким образом, использование i в формулах тригонометрических функций позволяет компактно и элегантно записывать их, особенно в контексте работы с комплексными числами.

Как использовать значение i в геометрии

Значение i, известное как мнимая единица, играет важную роль в математике и науке. В геометрии, i используется в комплексных числах для представления точек на комплексной плоскости.

Комплексные числа представляются в виде a + bi, где a и b — это действительные числа, а i — мнимая единица. Когда i возведено в квадрат, оно равно -1.

В геометрии, комплексные числа используются для представления векторов или точек на плоскости, где действительная часть a — это координата x, а мнимая часть b — это координата y.

Комплексные числа можно представить в виде таблицы, где в первом столбце указано действительное число a, во втором столбце — мнимое число bi, а в третьем столбце — результат сложения a+bi.

abia + bi

2	3i	2 + 3i
-1	4i	-1 + 4i
5	2i	5 + 2i

Использование комплексных чисел и мнимой единицы позволяет решать геометрические задачи, такие как нахождение расстояния между двумя точками, вращение объектов вокруг точки или масштабирование.

Значение i в геометрии открывает новые возможности для анализа и решения задач. Оно позволяет работать с комплексными плоскостями и решать задачи, которые были бы невозможны с использованием только действительных чисел.

Применение комплексных чисел с i в геометрических задачах

Комплексные числа с i, также известные как мнимые числа, имеют важное применение в геометрии. Они позволяют представлять точки на плоскости и выполнять различные операции над ними.

Для начала, давайте вспомним, что комплексное число состоит из действительной и мнимой частей. Действительная часть представляет собой горизонтальную координату точки на плоскости, а мнимая часть — вертикальную координату.

Одной из основных операций, которую можно выполнять с комплексными числами, является сложение. Когда мы складываем два комплексных числа, мы просто складываем их действительные и мнимые части отдельно. Например, если у нас есть комплексное число z1 = a + bi и комплексное число z2 = c + di, то их сумма будет равна z1 + z2 = (a + c) + (b + d)i.

Применение комплексных чисел с i в геометрических задачах позволяет нам легко представлять и манипулировать точками на плоскости. Например, мы можем использовать комплексные числа для нахождения расстояния между двумя точками или для нахождения координаты середины отрезка между двумя точками.

Также, комплексные числа с i могут быть использованы для представления геометрических фигур, таких как окружности и эллипсы. Мы можем использовать комплексные числа для нахождения радиуса и центра окружности, а также для определения фокусов и полуосей эллипса.

Одним из примеров применения комплексных чисел с i в геометрии является решение задачи о вращении точки вокруг начала координат. Для этого мы можем использовать умножение комплексного числа на другое комплексное число, представляющее угол поворота. Это позволяет нам легко определить новые координаты вращенной точки.

ПримерОписание

z1 + z2	Сложение двух комплексных чисел
z1 * z2	Умножение двух комплексных чисел
|z1|	Модуль комплексного числа

Использование комплексных чисел с i в геометрических задачах делает решение этих задач более эффективным и интуитивно понятным. Они позволяют нам работать с точками и фигурами на плоскости с помощью алгебраических операций и упрощают решение сложных геометрических задач.

Видео по теме:

Вопрос-ответ:

Зачем нужна буква i в математике?

Буква i в математике используется для обозначения мнимой единицы, которая представляет собой квадратный корень из -1. Мнимая единица является важным понятием в алгебре и имеет множество применений в различных областях математики и физики.

Как использовать букву i в алгебре?

В алгебре буква i используется для обозначения мнимых чисел. Мнимые числа представляют собой комбинации действительных чисел и мнимой единицы i. Например, число 3 + 4i, где 3 — действительная часть, а 4i — мнимая часть. С помощью мнимых чисел можно выполнять операции сложения, вычитания, умножения и деления, а также решать уравнения и решать задачи из различных областей науки и техники.

Как работать с комплексными числами?

Для работы с комплексными числами необходимо знать основные операции: сложение, вычитание, умножение и деление. Для сложения и вычитания комплексных чисел необходимо сложить или вычесть их действительные и мнимые части по отдельности. Для умножения двух комплексных чисел необходимо применить формулу разложения произведения суммы. Деление комплексных чисел можно осуществить путем умножения их на конъюгированные значения. Комплексные числа также могут быть представлены в полярной форме с помощью модуля и аргумента.

В каких областях науки и техники применяют комплексные числа?

Комплексные числа широко применяются в различных областях науки и техники. Они используются в электротехнике и электронике для моделирования и анализа электрических цепей. Кроме того, комплексные числа применяются в физике для описания колебаний, волн и сигналов. Они также находят применение в математическом моделировании, криптографии и других областях, где требуется работа с действительными и мнимыми числами.

Значение i в физике

Мнимые числа широко применяются в физике, особенно в теории поля и квантовой механике. В этих областях мнимые числа используются для описания волновых функций, состояний частиц и электромагнитных полей.

Мнимая единица также используется в комплексных числах и комплексном анализе, которые являются неотъемлемой частью физических законов и уравнений. Она позволяет выполнять математические операции с комплексными числами, такие как умножение, деление и возведение в степень.

Понимание мнимой единицы и ее значения i в физике позволяет исследователям и инженерам эффективно описывать и предсказывать различные физические явления и создавать новые технологии и материалы.

Использование комплексных чисел с i в физических уравнениях

Комплексные числа с мнимой единицей i находят широкое применение в физических уравнениях, где они позволяют моделировать поведение систем, которые не могут быть описаны только действительными числами.

Одной из областей применения комплексных чисел в физике является электромагнетизм. Уравнения Максвелла, описывающие электромагнитные поля, содержат комплексные числа при рассмотрении переменных полей во времени. Использование комплексных чисел позволяет учесть как активную компоненту поля (связанную с энергией), так и реактивную компоненту (связанную с электрическими и магнитными полями).

Комплексные числа также широко используются в квантовой механике для описания вероятностей и амплитуд. Волновая функция, описывающая состояние квантовой системы, может быть представлена комплексным числом. Использование комплексных чисел позволяет учесть как волновые процессы, так и вероятностные характеристики квантовых систем.

Также комплексные числа с i находят применение в теории управления и волновой оптике. В уравнениях управления комплексные числа позволяют учесть фазовые сдвиги и динамику систем. Волновая оптика использует комплексные числа для описания амплитуд и фаз световых волн.

Использование комплексных чисел с i в физических уравнениях позволяет более точно и полно описывать различные физические явления и взаимодействия между ними.