Что такое сопряженное в математике

Сопряженное число в математике — это число, полученное при замене знаков между вещественной и мнимой частями комплексного числа. Оно является основным понятием в теории комплексных чисел и имеет важное значение при решении задач из различных областей математики и физики.

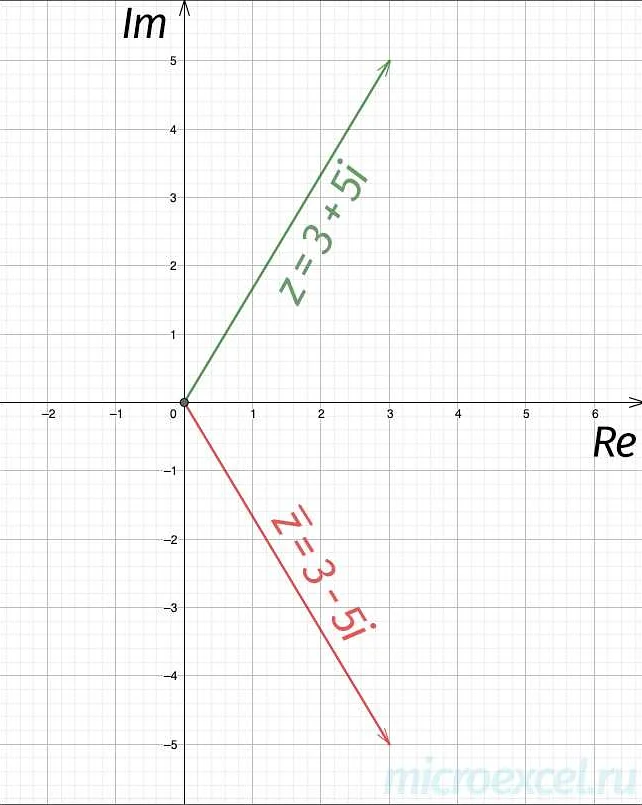
Сопряженное – это термин, часто используемый в математике, который означает отношение, связанное с комплексными числами. Сопряженное комплексного числа z обозначается как z* и представляет собой число, полученное изменением знака мнимой части числа z.

В более общем смысле, сопряженное также может означать отношение между объектами, где один объект является спутником или дополнением другого. В математике, сопряженное часто используется для описания отношений между геометрическими фигурами, алгебраическими структурами и даже функциями.

Например, в геометрии, сопряженное отношение может описывать отражение фигуры относительно прямой или плоскости. В алгебре, сопряженное часто используется для описания отношений между элементами алгебраических систем, таких как комплексные числа, кольца или поля.

Важно отметить, что понятие сопряженного может иметь различные значения в разных областях математики, и его использование зависит от контекста задачи. В любом случае, сопряженное отношение играет важную роль во многих областях математики и позволяет более глубоко понять связи и свойства различных математических объектов.

Сопряженное в математике: определение и примеры

Сопряженное пространство — это пространство, обратное по отношению к данному линейному пространству. Оно состоит из линейных функционалов, которые действуют на элементы данного пространства и превращают их в числа. Линейный функционал — это линейное отображение из данного пространства в поле, над которым оно определено. Сопряженное пространство позволяет рассматривать элементы пространства как функции на нем, которые могут быть интегрированы или умножены на другие функции.

Сопряженный оператор — это оператор, который связывает два сопряженных пространства. Он действует на элементы одного пространства и преобразует их в элементы другого пространства. Сопряженный оператор имеет связь с исходным оператором через сопряженность пространств: для каждого элемента исходного пространства, сопряженный оператор определяет элемент сопряженного пространства, который действует на этот элемент исходного пространства.

Примером сопряженного пространства является пространство непрерывных функций на отрезке [a, b] с весом и сопряженного оператора — интегральный оператор с ядром.

ПространствоСопряженное пространствоСопряженный оператор

Пространство непрерывных функций на отрезке [a, b] с весом

Пространство интегрируемых функций на отрезке [a, b] с весом

Интегральный оператор с ядром

Таким образом, сопряженное в математике играет важную роль при рассмотрении линейных пространств и операторов в них. Оно позволяет рассматривать элементы пространств как функции на них и определяет связь между пространствами через сопряженность исходного пространства и сопряженного оператора.

Видео по теме:

Что такое сопряженное в математике?

В линейной алгебре, сопряженное относится к операции, которая преобразует вектор в другой вектор, сохраняя некоторые свойства. Например, сопряженное векторное пространство — это пространство, в котором можно определить скалярное произведение между векторами.

В функциональном анализе, сопряженное относится к пространству, состоящему из линейных функционалов на данном пространстве. Линейный функционал — это отображение, которое сопоставляет каждому элементу пространства некоторое число.

В теории вероятностей, сопряженное распределение относится к паре распределений, которые обладают некоторыми специальными свойствами. Например, сопряженное распределение может быть использовано для нахождения апостериорного распределения в байесовской статистике.

Таким образом, сопряженное в математике — это понятие, которое связывает различные области математики и является основой для определения различных структур и операций.

Определение сопряженного числа

Если дано комплексное число вида a + bi, где a и b — действительные числа, то его сопряженным числом будет a — bi.

Таким образом, сопряженное число обладает теми же действительной частью, но противоположной мнимой частью.

Примеры:

Для числа 3 + 4i сопряженным числом будет 3 — 4i.

Для числа -2 — 7i сопряженным числом будет -2 + 7i.

Вопрос-ответ:

Что такое сопряженное в математике?

Сопряженное число – это число, получающееся из данного числа изменением знака мнимой части исходного числа. Если исходное число имеет вид a + bi, где a и b – действительные числа, то сопряженное число будет иметь вид a — bi.

Какую роль играют сопряженные числа в математике?

Сопряженные числа в математике имеют множество применений. Они используются, например, для упрощения выражений с комплексными числами, для решения уравнений с комплексными корнями, а также для определения симметричности относительно действительной оси на комплексной плоскости.

Можно ли взять сопряженное отрицательного числа?

Да, сопряженное отрицательного числа можно взять. Если исходное число имеет вид -a + bi, где a и b – действительные числа, то сопряженное число будет иметь вид -a — bi.

Какие примеры сопряженных чисел можно привести?

Примеры сопряженных чисел в математике могут быть следующими: для числа 3 + 2i сопряженным будет 3 — 2i; для числа -4 — 7i сопряженным будет -4 + 7i; для числа 2 сопряженным будет 2.

Свойства сопряженного числа

Сопряженное число обладает несколькими важными свойствами:

1. Сумма числа и его сопряженного равна удвоенной вещественной части числа.
2. Произведение числа и его сопряженного равно квадрату модуля числа.
3. Разность числа и его сопряженного равна удвоенной мнимой части числа.
4. Число и его сопряженное имеют одинаковую мнимую часть и противоположные вещественные части.
5. Модуль числа и его сопряженного равны.
6. Модуль произведения числа и его сопряженного равен квадрату модуля числа.

Эти свойства позволяют использовать сопряженные числа для решения различных задач и упрощения вычислений в математике и физике.

Сопряженное комплексное число

Сопряженное комплексное число обладает следующими свойствами:

1. Сумма числа $z$ и его сопряженного числа $\bar{z}$ равна двойной вещественной части числа $z$: $z + \bar{z} = 2a$.
2. Произведение числа $z$ и его сопряженного числа $\bar{z}$ равно квадрату модуля числа $z$: $z \cdot \bar{z} = (a^2 + b^2)$.
3. Если $z$ является чисто мнимым числом, то его сопряженное число $\bar{z}$ равно числу $-z$.

Сопряженное комплексное число находит применение в различных областях математики и физики, например, в алгебре, теории вероятности, электротехнике, оптике и других.

Примеры сопряженных чисел

В математике существует несколько примеров сопряженных чисел:

1. Комплексно-сопряженные числа. Комплексно-сопряженное число — это число, в котором мнимая часть меняет знак. Например, комплексно-сопряженными числами являются пары чисел (3 + 2i) и (3 — 2i). В этих парах реальные части чисел равны, а мнимые части отличаются только знаком.
2. Алгебраически сопряженные числа. Алгебраически сопряженное число — это число, которое получается из исходного числа путем смены знака у всех его иррациональных компонентов. Например, алгебраически сопряженным числом для числа 2 + √3 будет число 2 — √3, так как исходное число содержит иррациональную компоненту √3, которая меняет знак.
3. Рационально сопряженные числа. Рационально сопряженное число — это число, которое получается из исходного числа путем обращения рациональной части и смены знака у иррациональной части. Например, рационально сопряженным числом для числа 5 + √2 будет число 5 — √2, так как рациональная часть числа 5 не меняется, а иррациональная часть √2 меняет знак.

Это лишь некоторые примеры сопряженных чисел. В математике существует еще много различных видов и примеров сопряженных чисел, которые используются в различных областях и задачах.

Сопряженное рациональное число

Примером сопряженных рациональных чисел являются пара 2 и 1/2. Умножив их, получим:

2 * 1/2 = 1

Таким образом, числа 2 и 1/2 являются сопряженными рациональными числами, так как их произведение равно 1.

Сопряженные множества

В математике сопряженное множество или дополнение множества A обозначается как A’. Сопряженное множество состоит из всех элементов, которые не принадлежат множеству A. Иными словами, сопряженное множество содержит все элементы универсального множества, кроме тех, которые принадлежат множеству A.

Для определения сопряженного множества необходимо знать универсальное множество, которое включает все возможные элементы. В противном случае невозможно определить, какие элементы должны быть исключены из универсального множества.

Примером сопряженного множества может служить множество натуральных чисел. Если универсальным множеством является множество всех целых чисел, то сопряженным множеством будет множество всех целых чисел, кроме натуральных чисел.

Множество AСопряженное множество A’

{1, 2, 3}	{-∞, 0, 4, 5, …}
{a, b, c}	{x, y, z, …}

В таблице приведены примеры сопряженных множеств для конкретных множеств A. В первом примере множество A содержит натуральные числа, а сопряженное множество A’ содержит все целые числа, кроме натуральных. Во втором примере множество A содержит буквы а, b и c, а сопряженное множество A’ содержит все остальные буквы алфавита.

Сопряженное операторное пространство

Сопряженное операторное пространство обладает рядом важных свойств. Во-первых, оно является произведением двух пространств: пространства операторов и пространства объектов. Во-вторых, оно обладает структурой векторного пространства, что позволяет выполнять операции сложения и умножения на скаляр. Кроме того, сопряженное операторное пространство обладает также свойством сопряженности, что позволяет определить дуальное отношение между операторным и сопряженным операторным пространствами.

Примером сопряженного операторного пространства является пространство сопряженных операторов линейного оператора. Для линейного оператора можно определить его сопряженный оператор, который действует на двойственном пространстве. Сопряженный оператор обладает свойством сопряженности, то есть для любых двух операторов A и B выполняется равенство: (A * B) = (B * A).

Сопряженное операторное пространство играет важную роль во многих областях математики и ее приложений, таких как функциональный анализ, квантовая механика и теория вероятностей.