Что сделал революционного в математике лобачевский

Революционные открытия Николая Лобачевского перевернули представление о геометрии и привели к возникновению неевклидовых геометрий. Узнайте, какие принципиальные изменения он внес в математику и как это повлияло на развитие науки.

Николай Иванович Лобачевский – выдающийся русский математик, чье имя тесно связано с революцией в геометрии. В то время, когда все ученые считали, что евклидова геометрия является единственным истиным представлением о пространстве, Лобачевский доказал, что существуют и другие виды геометрии, отличные от евклидовой.

Основной вклад Лобачевского в математику заключается в разработке геометрии, которая стала известна как геометрия Лобачевского или неевклидова геометрия. Он доказал, что существуют геометрические системы, в которых не выполняются аксиомы евклидовой геометрии, в частности, аксиома о параллельных линиях. Это открытие перевернуло представление о пространстве и положило начало новой эпохе в геометрии.

Лобачевский развил свою теорию геометрии в нескольких работах, в которых он подробно изучал свойства и законы неевклидовой геометрии. Его исследования привели к созданию новых методов и инструментов для анализа и построения геометрических объектов в неевклидовых пространствах. Это позволило математикам более глубоко понять природу пространства и открыть новые горизонты в изучении геометрии.

«Исследование в области геометрии, в котором я работаю уже много лет, указывает на то, что существуют различные виды геометрии, отличные от евклидовой. Возможно, в будущем эти новые виды геометрии окажутся еще более полезными и важными, чем евклидова геометрия» – писал Лобачевский в одной из своих работ.

Сегодня геометрия Лобачевского широко используется в различных областях науки и техники, включая физику, космологию, компьютерную графику и теорию относительности. Она позволяет рассматривать пространство с учетом неевклидовых свойств и решать задачи, которые невозможно решить с помощью евклидовой геометрии. Безусловно, открытия Лобачевского имели огромное значение для развития математики и открыли новые горизонты в изучении пространства и его свойств.

Революционные идеи Лобачевского

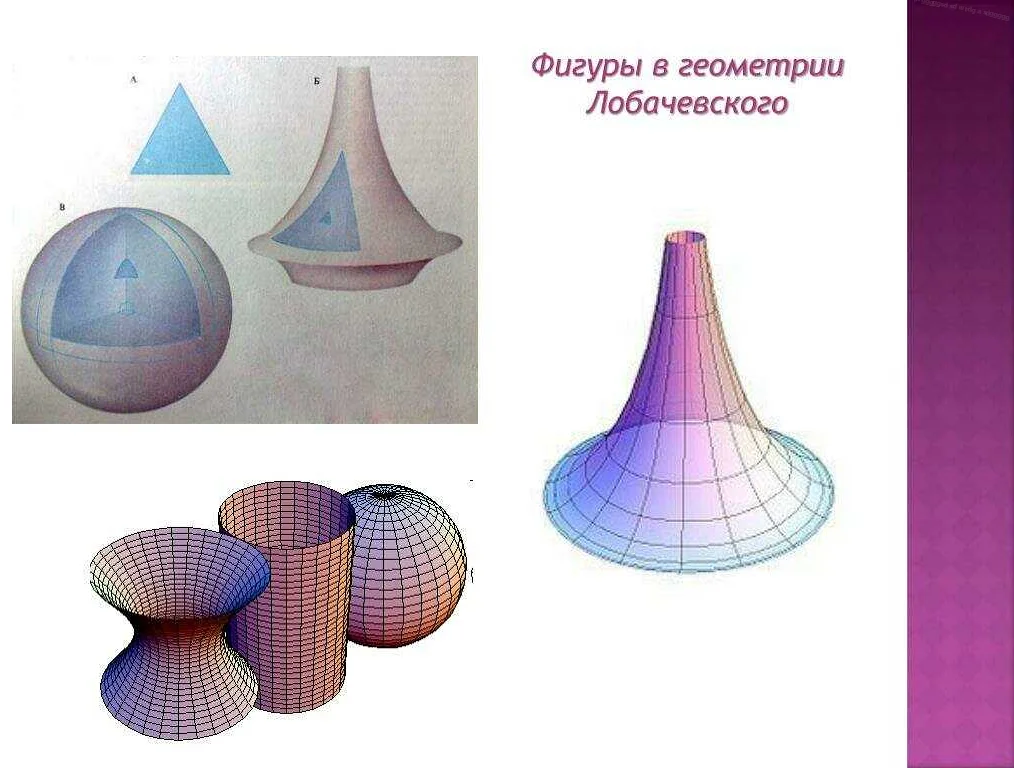
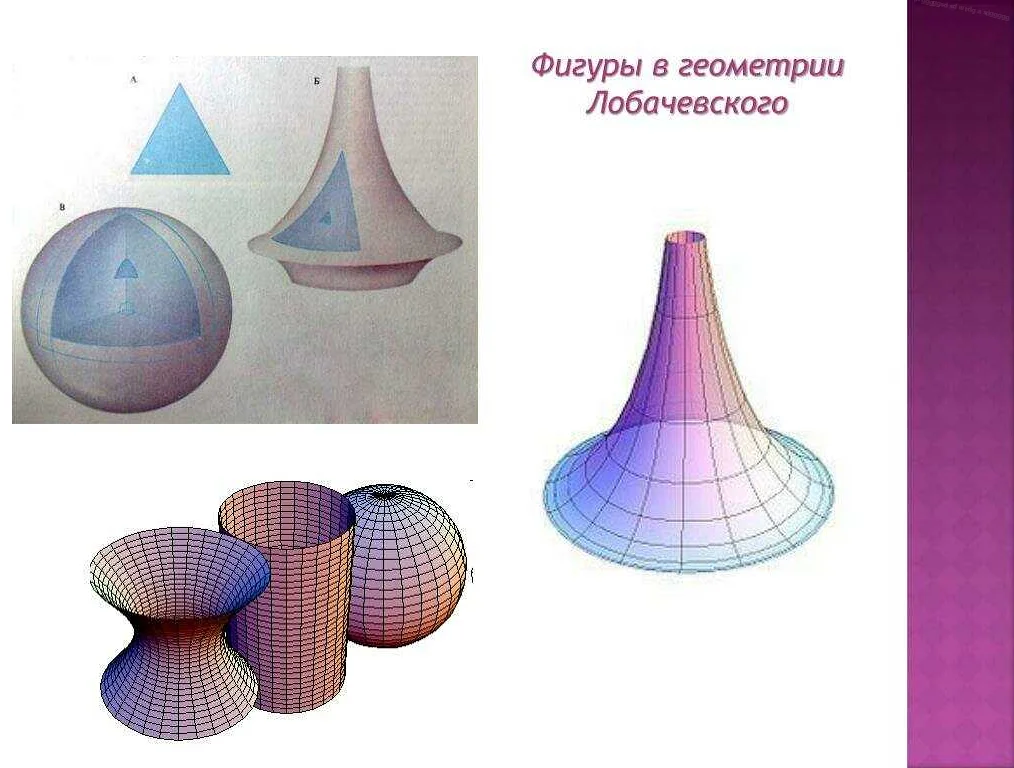
Николай Иванович Лобачевский был выдающимся русским математиком, который внес значительный вклад в развитие геометрии. Его работы открыли новые горизонты и перевернули привычные представления о пространстве и геометрии.

Одной из главных революционных идей Лобачевского была его неевклидова геометрия. Он смог создать систему, в которой аксиома параллельных линий не выполнялась. Это означало, что в его геометрии существовали несколько параллельных линий, проходящих через данную точку. Таким образом, он доказал, что существуют альтернативные модели пространства, в которых геометрические свойства могут отличаться от евклидовой геометрии.

Другой важной идеей Лобачевского было представление о бесконечности. Он развил концепцию бесконечно удаленных точек и линий, которые не имели определенного конца или предела. Это позволило ему создать новую геометрическую систему, в которой пространство было бесконечным и неограниченным.

Третьей важной идеей Лобачевского было его представление о геометрии как абстрактной науке. Он считал, что геометрия должна изучаться не только через практические применения, но и как самостоятельная наука, основанная на логических законах и математических принципах.

Все эти революционные идеи Лобачевского существенно изменили представление о геометрии и пространстве, и его работы продолжают влиять на современную математику и науку в целом.

Видео по теме:

Новые горизонты геометрии

Иван Иванович Лобачевский был выдающимся математиком XIX века, который совершил революцию в геометрии. В отличие от классической евклидовой геометрии, Лобачевский разработал неевклидову геометрию, которая открыла новые горизонты для математического и физического исследования.

Особенность неевклидовой геометрии заключается в том, что в ней отсутствует пятый постулат Евклида, так называемый аксиома параллельности. Это позволяет рассмотреть геометрию на плоскости с разными свойствами прямых, в том числе и с неограниченной геометрией, где существуют бесконечно далекие параллельные прямые.

Открытие неевклидовой геометрии Лобачевским имело огромное значение для развития математики и физики. Оно позволило рассмотреть новые модели пространства и времени, а также исследовать гипотезы, которые были недоступны в рамках евклидовой геометрии.

Несмотря на сопротивление некоторых математиков и философов, неевклидова геометрия стала основой для развития релятивистской физики Альберта Эйнштейна, который использовал ее в своей теории относительности. Таким образом, Лобачевский открыл новые горизонты для геометрии и сделал неоценимый вклад в развитие науки.

Альтернатива Евклидовой геометрии

Вместо этого Лобачевский предложил взять отрицание этого постулата, что привело к так называемой геометрии Лобачевского или гиперболической геометрии. В этой геометрии выполняются все остальные постулаты Евклида, кроме пятого.

Главным следствием отклонения от пятого постулата является то, что в гиперболической геометрии существуют несколько параллельных прямых, проходящих через одну точку. Это отличает гиперболическую геометрию от евклидовой, в которой существует только одна параллельная прямая.

Альтернативная геометрия Лобачевского имела огромное значение для математики и философии. Она позволила расширить представления о возможных геометрических структурах и открыть новые горизонты для исследований.

Сегодня гиперболическая геометрия находит применение в различных областях науки и техники, включая физику, компьютерную графику и космологию. Она также стала источником вдохновения для многих математиков и философов, открывая новые возможности для изучения структуры пространства и возможных вариантов его организации.

Отрицательная кривизна пространства

В геометрии с отрицательной кривизной пространства сумма углов треугольника будет меньше 180 градусов, а параллельные прямые могут пересекаться. Это означает, что в такой геометрии пространство может иметь отрицательную кривизну, а значит, оно может быть «вогнутым».

Открытие Лобачевского позволило расширить представления о возможных типах геометрии и открыть новые горизонты в математике. Геометрия с отрицательной кривизной нашла применение в различных областях, таких как теория относительности и неевклидова физика.

Важно отметить, что отрицательная кривизна пространства не означает его недостаточность или ошибку, а является лишь одним из возможных свойств. Благодаря исследованиям Лобачевского мы смогли понять, что мир геометрии гораздо более разнообразен и сложен, чем мы предполагали раньше.

Параллельные линии и их свойства

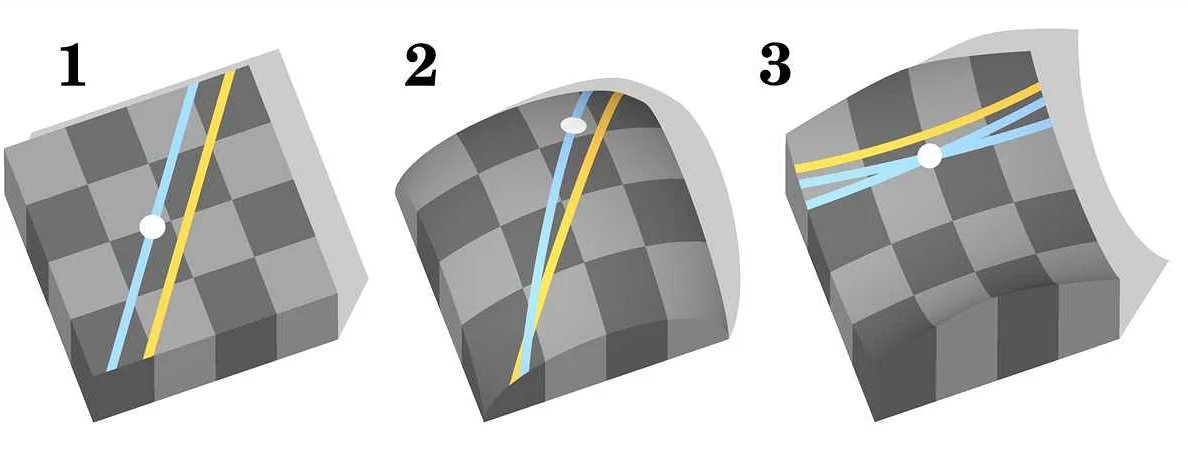
В геометрии Евклида существовало представление о том, что через точку вне прямой можно провести только одну прямую, параллельную данной. Однако Лобачевский открыл новое, революционное свойство параллельных линий.

Основное свойство параллельных линий, открытое Лобачевским, заключается в том, что через одну точку вне прямой можно провести бесконечно много прямых, параллельных данной. Это свойство было доказано математически и стало фундаментальным для новой геометрии, названной геометрией Лобачевского.

Геометрия Лобачевского отличается от геометрии Евклида тем, что в ней справедливо новое утверждение: через одну точку вне прямой можно провести не только одну, но и бесконечно много прямых, параллельных данной. Это свойство лежит в основе неевклидовой геометрии и открыло новые горизонты в математике.

СвойствоОписание

1	Параллельные линии находятся в одной плоскости и никогда не пересекаются.
2	Через одну точку вне прямой можно провести бесконечное количество прямых, параллельных данной.

Изучение свойств параллельных линий и геометрии Лобачевского имеет важное значение для различных областей науки и техники, таких как физика, информатика, астрономия и другие.

Влияние Лобачевского на современную математику

Ранее считалось, что евклидова геометрия является единственным способом описания пространства. Но Лобачевский показал, что существуют другие возможности. Он разработал геометрию, которая основывается на постулате о параллельных прямых, но отличается от евклидовой геометрии своими особенностями. Он доказал, что в такой геометрии сумма углов треугольника может быть меньше или больше 180 градусов, и введение понятия гиперболической геометрии.

Эти открытия Лобачевского имели огромное значение для математики и других наук. Они позволили развить новые направления и методы исследования. Неевклидова геометрия стала основой для развития дифференциальной геометрии, топологии и теории относительности. Она нашла применение в физике, астрономии, информатике и других областях.

Современная математика не может обойти вклад Лобачевского в развитие науки. Его открытия помогли пересмотреть привычное представление о пространстве и расширили возможности математического аппарата. Исследователи продолжают разрабатывать и применять неевклидову геометрию, внося новые открытия и улучшая методы анализа и моделирования.

Применение неевклидовой геометрииОбласть применения

Теория относительности	Физика
Геодезия	География
Теория кодирования	Информатика
Теория игр	Экономика

Влияние Лобачевского на современную математику неоценимо. Его открытия и идеи продолжают вдохновлять исследователей и вносить существенный вклад в развитие науки. Он показал, что существует множество возможностей и подходов к изучению математики, и его работы оставляют глубокий след в истории науки.

Применение геометрии Лобачевского в различных областях

Геометрия Лобачевского, основанная на неевклидовой геометрии, имеет широкий спектр применения в различных областях. Ее открытия и идеи Лобачевского сыграли важную роль в развитии науки и нашли свое применение в следующих областях:

1. Теория относительности: Геометрия Лобачевского стала фундаментальным инструментом в разработке и понимании теории относительности Альберта Эйнштейна. Ее применение позволило ученым представить пространство-время как неевклидову геометрическую структуру, что привело к революционным открытиям в физике.
2. Криптография: Геометрия Лобачевского нашла свое применение в криптографии, науке о защите информации. Открытия Лобачевского позволяют разрабатывать и анализировать криптографические алгоритмы, основанные на неевклидовых пространствах.
3. Космология: Идеи Лобачевского применяются в исследованиях космологии и изучении структуры Вселенной. Геометрия Лобачевского позволяет ученым представить неевклидовое пространство, что помогает в понимании законов развития Вселенной и формирования галактик.
4. Робототехника: Применение геометрии Лобачевского в робототехнике позволяет разрабатывать эффективные алгоритмы планирования движения для роботов в трехмерном пространстве. Это особенно важно для роботов, работающих в сложных условиях, например, в автономных автомобилях.
5. Теория игр и экономика: Геометрия Лобачевского находит свое применение в теории игр и экономике, где анализируются различные стратегии и взаимодействия между участниками. Идеи Лобачевского помогают ученым по-новому взглянуть на взаимодействия и развитие системы.

Таким образом, геометрия Лобачевского имеет важное значение в различных областях науки и технологий. Ее открытия и идеи помогают ученым расширить границы знаний и применить новые подходы в решении сложных задач.

Критика и отрицание Лобачевским аксиом Евклида

Николай Иванович Лобачевский, русский математик и геометр XIX века, внес революционные изменения в мир математики, в особенности в геометрию. Одной из самых значимых его научных открытий стала критика и отрицание аксиом Евклида, который считался фундаментом геометрии веками.

Евклидова геометрия основывалась на пяти аксиомах, которые считались неоспоримыми и неизменными. Однако Лобачевский начал сомневаться в их абсолютной истинности и предложил новую систему аксиом, противоположную аксиомам Евклида.

В частности, Лобачевский отрицал пятую аксиому Евклида – «через любую точку, не лежащую на прямой, можно провести только одну прямую, параллельную данной». Он предложил новую аксиому, согласно которой через данную точку можно провести бесконечное количество прямых, параллельных данной.

Такое отрицание аксиомы Евклида привело к созданию новой геометрии, которую назвали неевклидовой геометрией или геометрией Лобачевского. В этой геометрии справедливым было утверждение, что сумма углов треугольника меньше 180 градусов, и параллельные прямые могут пересекаться.

Это открытие Лобачевского имело огромное значение для развития математики и научных представлений о пространстве. Оно позволило расширить границы геометрии и привело к появлению новых разделов математики, таких как неевклидова геометрия и теория относительности.

Лобачевский своей критикой аксиом Евклида положил начало новому пониманию пространства, которое открыло для математики и науки в целом новые горизонты и возможности. Его открытие стало одним из важнейших в истории математики и оказало существенное влияние на развитие научного мышления.

Наследие Лобачевского: новые подходы к изучению пространства

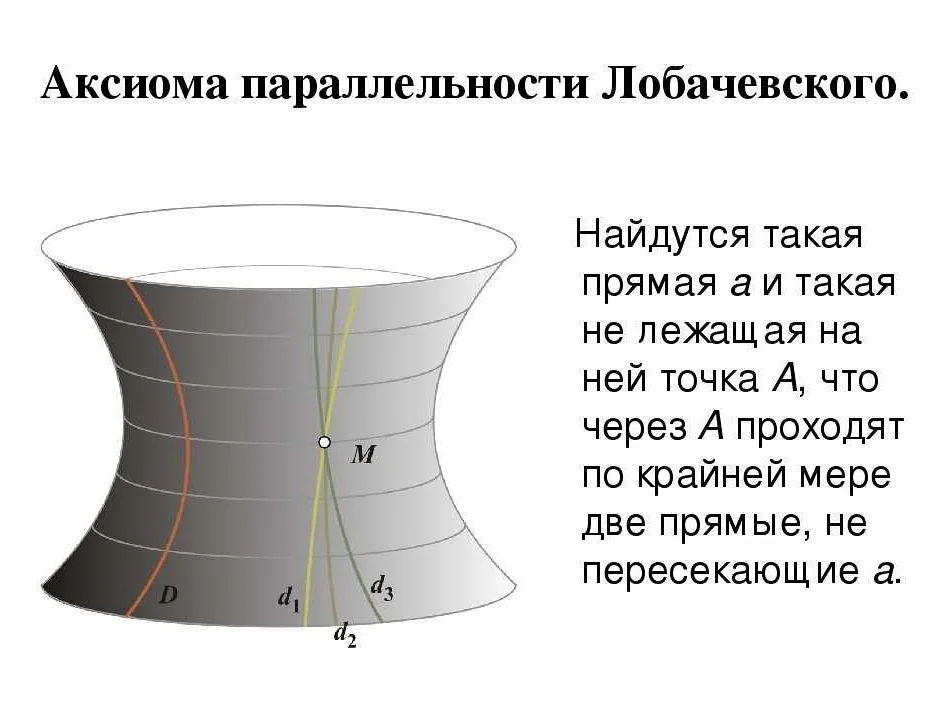
Известная как геометрия Лобачевского или гиперболическая геометрия, эта система исследовала пространство, в котором аксиома параллельности не выполняется. В результате было открыто, что существует множество возможностей для геометрических свойств и отношений, которые не были доступны в евклидовой геометрии.

Это наследие Лобачевского привело к новым подходам в изучении пространства. Ученые начали исследовать геометрические системы с различными аксиомами, открывая новые виды геометрии и исследуя их свойства. Так, появились эллиптическая геометрия и геометрия Римана, которые также отличаются от евклидовой геометрии.

Наследие Лобачевского не только расширило представление о пространстве, но и подтолкнуло развитие других областей математики и науки в целом. Исследования в области топологии, теории групп и дифференциальной геометрии стали неразрывно связаны с новыми подходами к изучению пространства, предложенными Лобачевским.

Сегодня наследие Лобачевского продолжает вдохновлять ученых и специалистов в различных областях. Изучение гиперболической геометрии и других неевклидовых геометрий не только позволяет лучше понять и описать физическое и математическое пространство, но и находит применение в различных сферах, включая компьютерную графику, робототехнику и космологию.

Наследие Лобачевского:Новые подходы к изучению пространства

Разработка негеометрической системы	Расширение представления о пространстве
Геометрия Лобачевского	Изучение геометрических систем с различными аксиомами
Эллиптическая геометрия и геометрия Римана	Развитие других областей математики и науки
Влияние на топологию, теорию групп и дифференциальную геометрию	Применение в компьютерной графике, робототехнике и космологии

Вопрос-ответ:

Кто такой Лобачевский?

Николай Иванович Лобачевский — русский математик, создатель геометрии Лобачевского, который внес огромный вклад в развитие математики и открыл новые горизонты в геометрии.

Чему посвящена статья о Лобачевском?

Статья посвящена жизни и научной деятельности Николая Ивановича Лобачевского, а также его вкладу в развитие математики и открытию новых горизонтов в геометрии.

Какие новые горизонты открыл Лобачевский в геометрии?

Лобачевский открыл новую форму геометрии — геометрию Лобачевского, которая отличается от классической евклидовой геометрии и имеет неевклидову основу. Он показал, что существуют пространства с неевклидовой геометрией, где выполняются различные аксиомы, отличные от аксиом евклидовой геометрии.

Какое значение имеет открытие Лобачевского для современной математики?

Открытие Лобачевского имеет огромное значение для современной математики. Оно позволило расширить представления о геометрии и открыть новые возможности в математическом исследовании. Геометрия Лобачевского нашла применение в различных областях, таких как теория относительности, топология и дифференциальная геометрия.