Математик лобачевский доказал что параллельные прямые пересекаются
Содержимое
- 1 Математик лобачевский доказал что параллельные прямые пересекаются
- 1.1 Математик Лобачевский
- 1.2 О жизни и научной деятельности
- 1.3 О геометрии и постулате Евклида
- 1.4 Основные идеи исследований Лобачевского
- 1.5 Открытие о параллельных прямых
- 1.6 Критика и согласие с открытием Лобачевского
- 1.7 Воздействие открытия на науку
- 1.8 Вопрос-ответ:
- 1.8.0.1 Как и когда Лобачевский доказал, что параллельные прямые пересекаются?
- 1.8.0.2 Каким образом Лобачевский доказал, что параллельные прямые пересекаются?
- 1.8.0.3 Почему Лобачевский пришел к выводу, что параллельные прямые пересекаются?
- 1.8.0.4 Какое значение имеет доказательство Лобачевского о пересечении параллельных прямых?
- 1.8.0.5 Какие последствия имеет доказательство Лобачевского о пересечении параллельных прямых?
- 1.8.0.6 Кто доказал, что параллельные прямые пересекаются?
- 1.8.0.7 Каким образом Лобачевский доказал, что параллельные прямые пересекаются?
- 1.9 Значение открытия для современной математики
- 1.10 Видео по теме:
Математик Лобачевский доказал, что параллельные прямые могут пересекаться. Узнайте, какое важное открытие сделал этот великий ученый и как оно изменило наше понимание геометрии.
Николай Иванович Лобачевский, выдающийся русский математик и геометр, стал первым, кто смог доказать, что параллельные прямые, оказывается, могут пересекаться. В то время, когда Евклидова геометрия считалась непоколебимой и единственно верной, Лобачевский открыл новый принцип, который перевернул мир математики.
Главное открытие Лобачевского, связанное с неевклидовой геометрией, дало начало развитию новой математической дисциплины. Он доказал, что если в евклидовой геометрии предполагается, что аксиома параллельности выполняется, то в неевклидовой геометрии можно сформулировать систему аксиом, в которой параллельные прямые пересекаются. Это открытие повлекло за собой революцию в понимании пространства и геометрии, и было одним из ключевых шагов в развитии математики.
Исследования Лобачевского имели глубокий воздействие на развитие математики и философии, и его работы открыли новые горизонты для геометрии и других областей науки. Он показал, что идеи, которые казались самоочевидными и неотъемлемыми, могут оказаться ошибочными, и настаивал на необходимости критического мышления и поиска новых подходов в науке и жизни.
Математик Лобачевский

Математик Николай Лобачевский (1792-1856) был российским ученым, который внес значительный вклад в развитие геометрии и математической логики. Он известен своими исследованиями в области неевклидовой геометрии, которая отличается от классической евклидовой геометрии.
В евклидовой геометрии справедливо утверждение, что параллельные прямые никогда не пересекаются. Однако Лобачевский доказал, что существует другой вид геометрии, в которой параллельные прямые могут пересекаться. Это стало возможным благодаря изменению пятого постулата Евклида, который определяет свойства параллельных линий.
Лобачевский предложил новую геометрию, которая получила название «гиперболической геометрии». В этой геометрии угол суммы треугольника всегда меньше 180 градусов, а сумма углов вокруг точки больше 360 градусов. Это противоречит теоремам евклидовой геометрии и открывает новые возможности для математических исследований.
Открытия Лобачевского имели огромное значение для развития математики и были важным шагом к развитию неевклидовой геометрии, которая впоследствии нашла практическое применение в физике и космологии. Сегодня гиперболическая геометрия используется в теории относительности и других науках для описания пространства с кривизной.
О жизни и научной деятельности
Математик Николай Иванович Лобачевский родился 1 декабря 1792 года в городе Нижний Новгород. С детства он проявлял большой интерес к математике и стремился разобраться в сложных проблемах этой науки.
Лобачевский учился в Казанском университете, где и начал свою научную карьеру. В 1826 году он был назначен ректором Казанского университета, что подтверждало его высокий уровень научных достижений и авторитет в области математики.
Основное достижение Лобачевского — это разработка геометрии, в которой аксиома параллельных прямых не выполняется. Он доказал, что параллельные прямые могут пересекаться, и тем самым изменил представление о пространстве и геометрии.
Лобачевский был уважаемым ученым и преподавателем. Он не только занимался научной деятельностью, но и активно участвовал в образовательной работе, привлекая к математике студентов и молодых ученых.
Весь свой жизненный путь Лобачевский посвятил математике. Он проводил много времени в научных исследованиях, публикации статей и разработке новых теорий. Его работа была признана важным вкладом в развитие математики и оказала огромное влияние на дальнейшие исследования в этой области.
Николай Иванович Лобачевский скончался 24 февраля 1856 года в Казани, но его научное наследие продолжает жить и развиваться до сих пор. Его открытия в геометрии имеют значительное значение не только для математики, но и для других областей науки и техники.
О геометрии и постулате Евклида

Один из этих постулатов, известный как «постулат о параллельных», давал определение параллельных прямых. Он гласил: «Через точку, не принадлежащую прямой, можно провести только одну прямую, параллельную данной». Этот постулат казался очевидным и не вызывал сомнений в течение многих веков.
Однако в 19 веке русский математик Николай Лобачевский доказал, что этот постулат не является единственно возможным. Он показал, что существует геометрия, в которой параллельные прямые могут пересекаться. Это стало одним из важнейших открытий в истории математики и привело к развитию неевклидовой геометрии.
Неевклидова геометрия оказалась применимой в физике и космологии, а также нашла свое применение в технических исследованиях. Она изменила наше представление о пространстве и позволила нам лучше понять его структуру и свойства.
Таким образом, открытие Лобачевским того, что параллельные прямые могут пересекаться, существенно расширило нашу геометрическую интуицию и показало, что истина в науке может быть относительной и зависеть от выбранной системы аксиом и постулатов.
Основные идеи исследований Лобачевского
Николай Иванович Лобачевский был выдающимся русским математиком и геометром, который внес значительный вклад в развитие геометрии. Одной из главных идей, которую Лобачевский разработал, было отрицание аксиомы Евклида о параллельных прямых.
Ранее считалось, что через одну точку можно провести только одну прямую, параллельную данной. Однако Лобачевский предположил, что через одну точку можно провести бесконечно много параллельных прямых. Он доказал, что если предположить существование параллельных прямых, которые никогда не пересекаются, то можно получить некоторые противоречивые утверждения.
Лобачевский представил новую геометрию, названную гиперболической геометрией. В гиперболической геометрии геометрические фигуры и свойства пространства существенно отличаются от привычной евклидовой геометрии.
Одним из главных результатов исследований Лобачевского стало доказательство того, что параллельные прямые на плоскости гиперболической геометрии пересекаются. Это оказалось принципиально новым и неожиданным результатом, который поставил под сомнение некоторые основные принципы геометрии Евклида.
Идеи Лобачевского имели огромное значение для дальнейшего развития математики и научного мышления в целом. Его работы стали отправной точкой для развития неевклидовых геометрий и имели огромное влияние на философию и фундаментальные науки.
Открытие о параллельных прямых
Российский математик Николай Лобачевский совершил значимое открытие в геометрии, доказав, что параллельные прямые могут пересекаться. Это открытие, сделанное в XIX веке, потрясло академическое сообщество и стало фундаментальным прорывом в математике.
В классической Евклидовой геометрии считалось, что параллельные прямые никогда не пересекаются. Однако Лобачевский подошел к этому вопросу с иной стороны и предложил новую геометрию, которая не была ограничена аксиомами Евклида. Он разработал геометрию на плоскости, в которой параллельные прямые могут пересекаться, и назвал ее геометрией Лобачевского.
Открытие Лобачевского имело большое значение для математики и философии, поскольку оно подвергло сомнению теории, которые казались неоспоримыми. Он показал, что существует несколько видов геометрии, и что их применимость зависит от контекста. Таким образом, Лобачевский расширил понимание геометрии и открыл новые возможности для ее применения.
Открытие Лобачевского о параллельных прямых стало одной из важнейших математических теорем и оказало влияние на развитие различных научных дисциплин. С его помощью удалось решить множество задач и проблем, которые ранее казались неразрешимыми.
Критика и согласие с открытием Лобачевского
Открытие Лобачевского о том, что параллельные прямые могут пересекаться, вызвало оживленные дискуссии в научном сообществе. С одной стороны, его открытие было встречено с восхищением и признанием его гениальности. Лобачевский положил начало новой геометрии, которая открыла двери для развития неевклидовой геометрии и имела глубокое влияние на развитие математики в целом.
С другой стороны, открытие Лобачевского вызвало и критику. Некоторые математики и ученые не принимали новую геометрию, так как она противоречила тривиальным и очевидным аксиомам Евклида. Они полагали, что только геометрия Евклида является истинной и все другие геометрии противоречат здравому смыслу и интуитивным представлениям.
Однако, с течением времени, открытие Лобачевского было все больше принято и ученые стали признавать его значимость. Используя математический аппарат Лобачевского, были сделаны множество открытий и достижений в различных областях науки и техники. Неевклидова геометрия стала незаменимым инструментом в изучении пространства и работе с комплексными системами.
Таким образом, открытие Лобачевского составляет важную часть научного наследия и способствовало развитию математики. Несмотря на начальные сомнения и критику, его открытие доказало свою ценность и привнесло новые знания и возможности в научный мир.
Воздействие открытия на науку
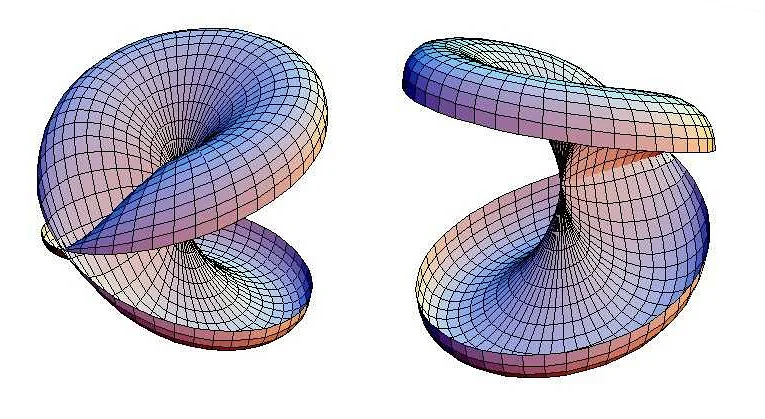
Открытие математиком Лобачевским того, что параллельные прямые могут пересекаться, имело огромное воздействие на развитие науки. Это открытие противоречило традиционной евклидовой геометрии, которая утверждала, что параллельные прямые никогда не пересекаются.
Открытие Лобачевского вызвало широкую дискуссию в научном сообществе и привело к революции в математике. Ранее считалось, что евклидова геометрия является единственно верной и абсолютной. Открытие Лобачевского показало, что существуют и другие геометрические системы, которые могут быть применены в реальном мире.
Открытие Лобачевского имело важное значение не только для математики, но и для физики и других научных дисциплин. Оно позволило развить новые модели и теории, которые ученые использовали для объяснения и предсказания различных явлений.
Воздействие открытия Лобачевского на науку было долгосрочным и привело к значительному прогрессу в понимании фундаментальных принципов и законов природы. Это открытие также показало, что наука всегда открыта для новых и неожиданных идей, которые могут изменить наше представление о мире.
Вопрос-ответ:
Как и когда Лобачевский доказал, что параллельные прямые пересекаются?
Лобачевский доказал это в своей работе «О началах геометрии». Данная работа была опубликована в 1829 году.
Каким образом Лобачевский доказал, что параллельные прямые пересекаются?
Лобачевский использовал неевклидову геометрию для доказательства этого факта. Он показал, что в геометрии с неевклидовыми аксиомами существуют параллельные прямые, которые пересекаются.
Почему Лобачевский пришел к выводу, что параллельные прямые пересекаются?
Лобачевский пришел к этому выводу, исследуя свойства неевклидовой геометрии. Свои результаты он опубликовал в работе «О началах геометрии». Он показал, что существуют модели, в которых параллельные прямые пересекаются.
Какое значение имеет доказательство Лобачевского о пересечении параллельных прямых?
Доказательство Лобачевского о пересечении параллельных прямых имеет важное значение для математики и геометрии. Оно показало, что неевклидова геометрия является возможной альтернативой классической евклидовой геометрии, и продемонстрировало, что аксиомы геометрии могут быть изменены.
Какие последствия имеет доказательство Лобачевского о пересечении параллельных прямых?
Доказательство Лобачевского о пересечении параллельных прямых привело к развитию неевклидовой геометрии и открытию новых математических концепций. Оно оказало значительное влияние на развитие общей теории относительности и применение геометрии в физике и других науках.
Кто доказал, что параллельные прямые пересекаются?
Доказательство того, что параллельные прямые пересекаются, было предложено русским математиком Николаем Ивановичем Лобачевским в 1829 году.
Каким образом Лобачевский доказал, что параллельные прямые пересекаются?
Лобачевский доказал это, введя в геометрию неевклидову модель, которая основывается на аксиомах, отличных от аксиом Евклида. В его модели, параллельные прямые действительно пересекаются.
Значение открытия для современной математики
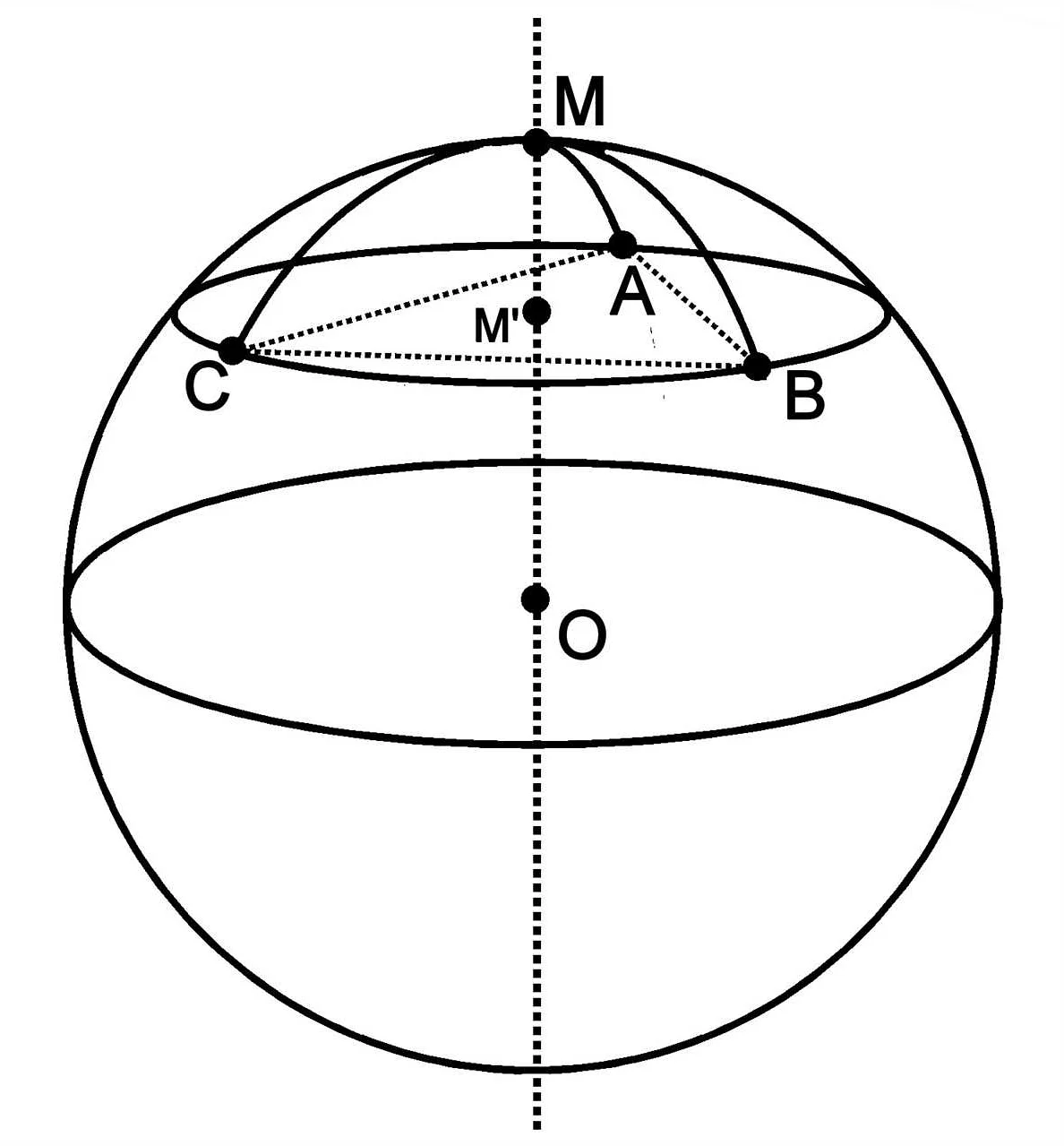
Открытие Николая Ивановича Лобачевского стало одним из важнейших вех в развитии математики. Его доказательство о том, что параллельные прямые могут пересекаться, перевернуло представление о геометрии и положило основу для развития неевклидовой геометрии.
Открытие Лобачевского имело огромное значение для современной математики. Оно позволило расширить границы геометрии и создать новую область исследований – неевклидову геометрию. Это открытие имело огромный вклад в развитие математической логики и анализа, а также нашло свое применение в других науках, таких как физика и астрономия.
Сейчас неевклидова геометрия широко применяется в различных областях науки и техники, включая компьютерную графику, криптографию, теорию относительности и многие другие. Открытие Лобачевского открыло новые горизонты для математики и стало отправной точкой для многих последующих исследований и открытий в этой области.
Таким образом, открытие Лобачевского оказало глубокое влияние на современную математику и научный прогресс в целом. Оно позволило пересмотреть устоявшиеся представления о геометрии и открыть новые возможности для дальнейших исследований и развития науки.

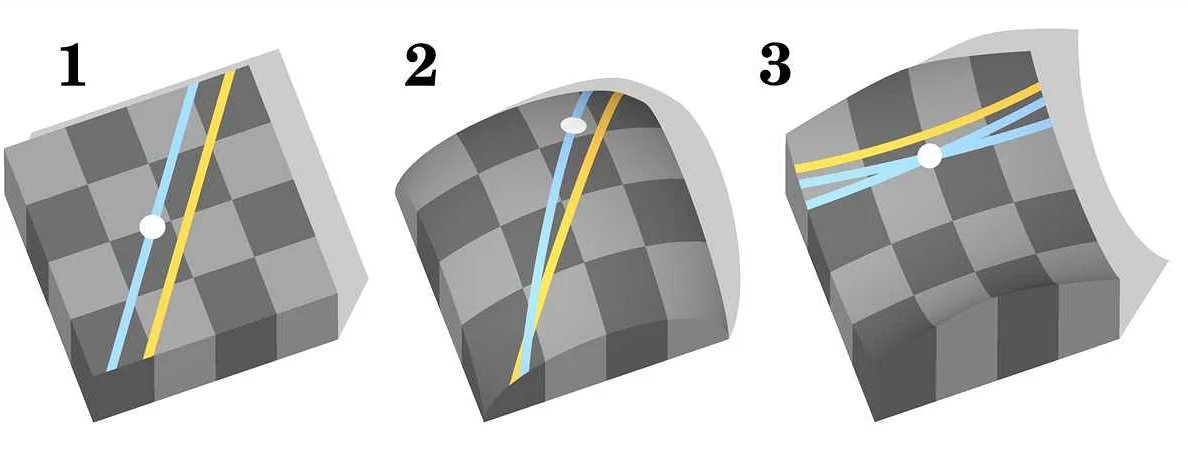
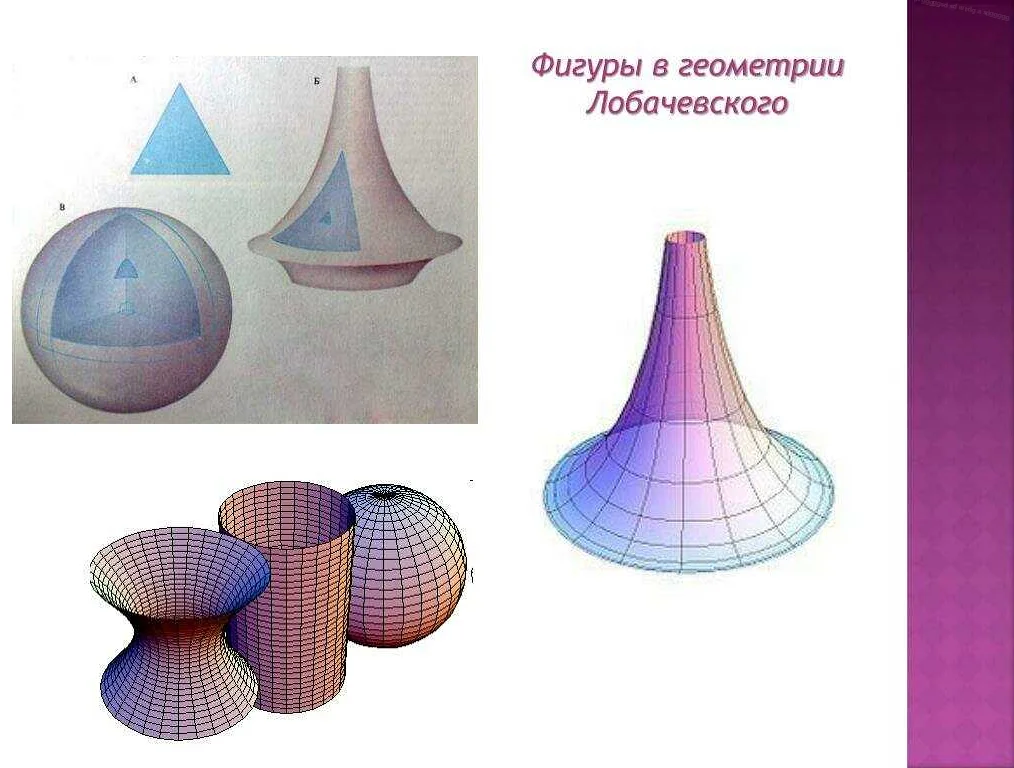


Математика всегда увлекала меня своей точностью и логикой. И вот, я наткнулся на интересную статью о Лобачевском и его открытии о параллельных прямых. Честно говоря, я всегда думал, что параллельные прямые не пересекаются вообще. Оказывается, это не так! Лобачевский доказал, что в геометрии на плоскости с неевклидовой метрикой, параллельные прямые могут пересекаться. Это открытие полностью изменило мое представление о геометрии и подтолкнуло меня к изучению более сложных математических концепций. Теперь я могу с уверенностью сказать, что мир математики бесконечен и полон открытий, которые могут перевернуть наше понимание окружающего нас пространства.
Увлекательно и захватывающе! Я всегда была увлечена миром математики, и открытия, которые делают ученые, всегда вызывают у меня интерес. Одним из таких открытий является теория Лобачевского о параллельных прямых, которая в корне меняет наше представление о геометрии. Доказательство Лобачевского о том, что параллельные прямые пересекаются, вызывает во мне невероятное волнение и удивление. Как женщина, я горжусь достижениями Лобачевского и его способностью видеть и понимать мир через призму математических формул и логики. Его открытие открывает двери к новым возможностям и переосмыслению привычных нам понятий о пространстве и геометрии. Я увлечена этой статьей и всегда готова изучать и погружаться в мир математики, который так близок к моему сердцу. Браво, Лобачевский, и спасибо за вашу важную работу!
Эта статья просто потрясающая! Я всегда думала, что параллельные прямые никогда не пересекаются, но оказывается, я ошибалась! Математик Лобачевский смог доказать, что это не так. Это действительно великое открытие! Я восхищаюсь талантом и умом ученых, которые способны найти такие невероятные решения. Теперь мне хотелось бы узнать больше об этом феномене. Каким образом Лобачевский смог это доказать? Какие были его исследования и эксперименты? Я уверена, что это очень интересно и я бы хотела глубже погрузиться в эту тему. Спасибо за такую увлекательную статью!
Удивительно, как математика может открывать нам новые грани реальности. Открытие Лобачевским того, что параллельные прямые на самом деле пересекаются, вроде бы противоречит нашему ежедневному восприятию мира. Но именно эта идея открывает перед нами новые возможности и меняет наше понимание геометрии. Математика — это наука, которая помогает нам разгадывать тайны и законы окружающего мира, и именно благодаря таким ученым, как Лобачевский, мы можем видеть вещи иначе и расширять свои познания. Не перестаю удивляться, насколько грандиозными и неожиданными могут быть открытия в науке. Большое спасибо ученым, которые открывают перед нами новые горизонты и расширяют наше понимание мира.