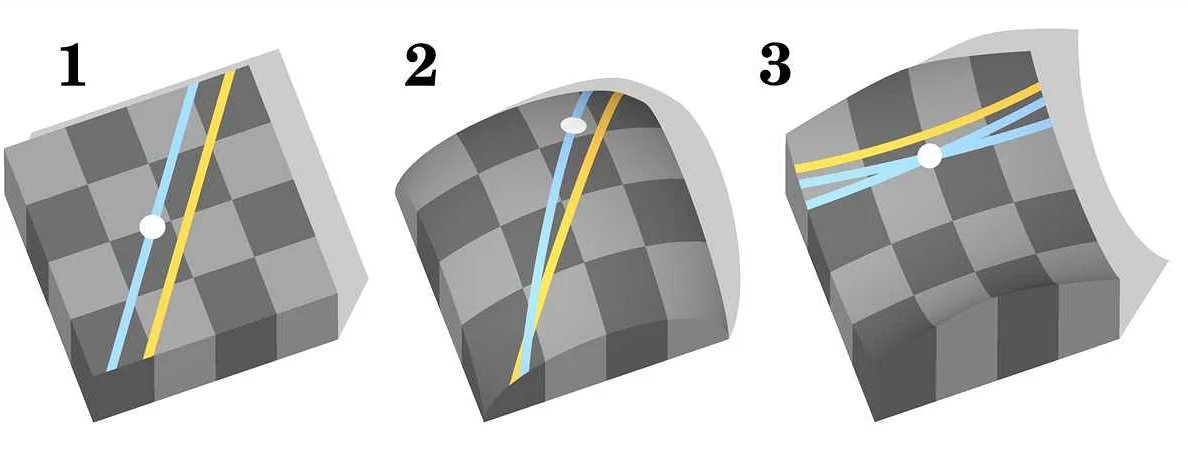
Может ли параллельная прямая пересечь другую линию? И гениальный математик Лобачевский дал на это ответ
Содержимое
- 1 Может ли параллельная прямая пересечь другую линию? И гениальный математик Лобачевский дал на это ответ
- 1.1 Математик Лобачевский и параллельные прямые
- 1.2 Видео по теме:
- 1.3 Жизнь и научная деятельность
- 1.4 Понятие параллельности
- 1.5 Вопрос-ответ:
- 1.5.0.1 Кто такой Математик Лобачевский?
- 1.5.0.2 Что такое неевклидова геометрия?
- 1.5.0.3 Что значит, что в евклидовой геометрии параллельные прямые не пересекаются?
- 1.5.0.4 Есть ли пересечение параллельных прямых в неевклидовой геометрии?
- 1.5.0.5 Какие тексты остались после Лобачевского, связанные с параллельными прямыми?
- 1.5.0.6 Какие последствия имеет отказ от постулата Евклида?
- 1.5.0.7 Как Лобачевский повлиял на развитие математики?
- 1.6 Проблемы Евклида
- 1.7 Реформулирование аксиом геометрии
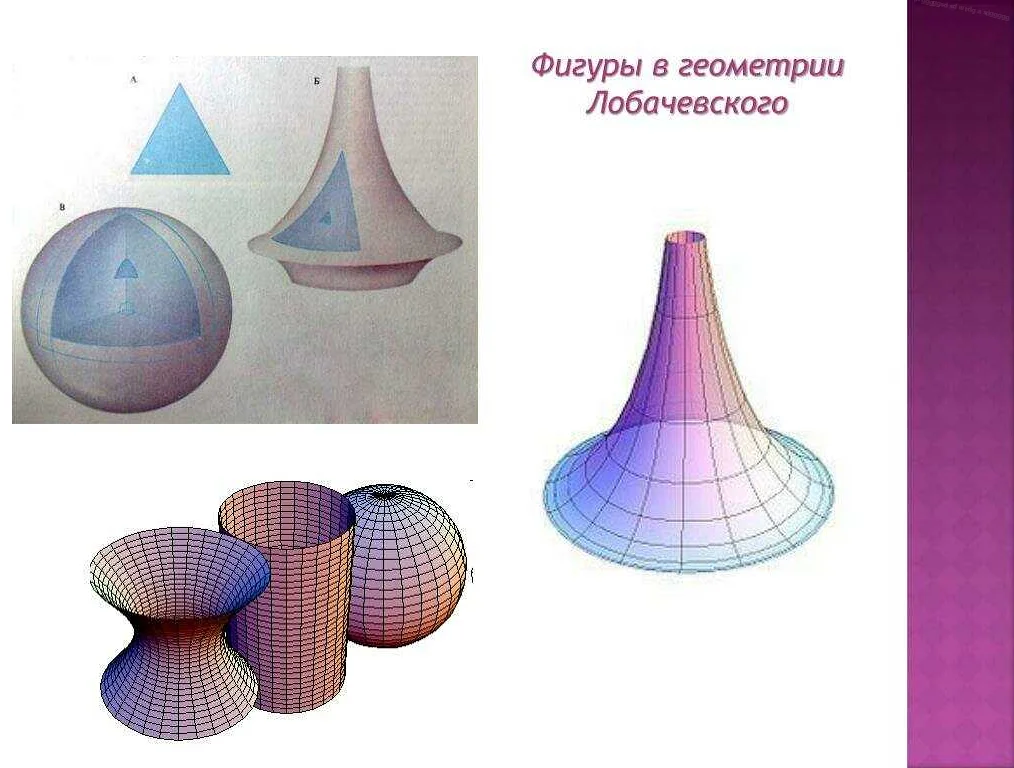
- 1.8 Геометрия Лобачевского
- 1.9 Пересечение прямых на плоскости
- 1.10 Линии и поверхности Лобачевского
- 1.11 Перспектива применения геометрии Лобачевского
- 1.12 Различия между геометрией Лобачевского и классической геометрией
- 1.13 Применение геометрии Лобачевского в современных науках
- 1.14 Выводы
Николай Лобачевский — знаменитый математик XIX века, разработавший геометрические теории о неевклидовых пространствах. Его открытия позволили убедительно доказать, что параллельные прямые действительно могут пересекаться, что противоречило традиционным представлениям евклидовой геометрии. Узнайте о революционном исследовании Лобачевского в нашей статье.
Николай Иванович Лобачевский — один из самых известных математиков XIX века. Он считается основателем неевклидовой геометрии, которая изменила наше представление о пространстве и открыла новые горизонты для науки и техники.
Одним из ключевых вопросов, которым занимался Лобачевский, был вопрос о пересечении параллельных прямых. В стандартной евклидовой геометрии, которую учат в школах, мы знаем, что две параллельные прямые никогда не пересекаются. Однако в неевклидовой геометрии это утверждение уже не такое очевидное.
Как же представляется мир в неевклидовой геометрии, и есть ли там пересечение параллельных прямых? Об этом и других важных вопросах мы расскажем в нашей статье.
«Далеко не всегда надо искать новые зеркала для наших глаз, чтобы увидеть чужую жизнь. Иногда для того, чтобы увидеть незнакомую действительность, достаточно поднять голову и посмотреть вокруг.» — Николай Иванович Лобачевский
Математик Лобачевский и параллельные прямые
Николай Иванович Лобачевский был российским математиком, который внес значительный вклад в геометрию. Одним из самых интересных его открытий стало доказательство того, что в геометрии, отличной от евклидовой, параллельные прямые могут пересекаться.
В евклидовой геометрии две прямые, которые находятся в одной плоскости и не пересекаются, считаются параллельными. Но Лобачевский показал, что при изменении некоторых аксиом, которые используются в евклидовой геометрии, прямые могут пересекаться. Такая геометрия называется неевклидовой.
В неевклидовой геометрии параллельные прямые пересекаются, и это приводит к изменению многих других геометрических свойств. Но такая геометрия нашла свое применение в физике и гравитации, и некоторые ученые считают ее более приближенной к реальности, чем евклидова геометрия.
Таким образом, открытие Лобачевского о том, что параллельные прямые могут пересекаться, оказало большое влияние на развитие математики и наше понимание геометрии.
Видео по теме:
Жизнь и научная деятельность
Николай Иванович Лобачевский (1792-1856) — выдающийся русский математик, который изучал геометрию и алгебру. Он родился в семье помещика и получил свое образование в Казанском университете, где впоследствии стал профессором и директором университетской библиотеки.
Лобачевский всю свою жизнь посвятил изучению двух областей математики: геометрии и теории чисел. Он разработал новую геометрию, с которой связано его имя и которую сейчас называют гиперболической геометрией. Его идеи и открытия революционизировали мировую математику и положили начало новой форме геометрии, отличной от привычной евклидовой геометрии.
Однако, Лобачевский не мог доказать свой теоремы о гиперболической геометрии из-за того, что она противоречила принципам евклидовой геометрии. Но в конечном итоге это привело к пониманию, что геометрические принципы, которыми мы руководствуемся, — всего лишь выбор нашего ума, а не абсолютная истина.
Кроме того, Лобачевский открыл новую область математики — геометрическую теорию чисел. Он дал определение функции Лобачевского и стал первым, кто раскрыл свойства конических секущих и касательных.
Хотя в его жизни не было достаточно признания, Лобачевский вошел в историю математики как великий ученый, который открыл новую область математики и изменил способ мышления, который позволил новым идеям и теориям прорваться в мировую математику.
Понятие параллельности
Параллельность – это свойство двух или более линий, находящихся на одной плоскости, не имеющих общих точек. Другими словами, параллельные линии расположены таким образом, что они не пересекаются и остаются одинаково удаленными друг от друга на всем протяжении.
На практике понятие параллельности находит применение в различных областях, включая геометрию, физику, инженерию и архитектуру. Например, в геометрии понятие параллельности используется для изучения свойств линий и углов, а в инженерии и архитектуре – для проектирования и строительства зданий и сооружений.
Понятие параллельности тесно связано с понятием угла, так как две параллельные линии образуют угол, равный 180 градусам. Кроме того, параллельные линии могут быть направлены вертикально, горизонтально или под наклоном к оси координат.
В математике особое внимание уделяется свойствам параллельных линий. Например, одной из основных теорем геометрии является теорема Планиметрии о параллельных линиях, которая утверждает, что при пересечении двух параллельных линий третья линия, пересекающая их, образует соответственные углы, равные между собой.
- Общие свойства параллельных линий:
- Они не пересекаются.
- Расстояние между ними постоянно на всем протяжении.
- Они находятся на одной плоскости.
Важное значение понятие параллельности имеет также в неевклидовой геометрии, которая изучает геометрические объекты, отличные от классической геометрии Евклида. Так, например, в геометрии Лобачевского параллельные линии могут пересекаться в одной точке, что противоречит классическим геометрическим законам.
Вопрос-ответ:
Кто такой Математик Лобачевский?
Николай Иванович Лобачевский был русским математиком-геометром, который считается одним из основателей неевклидовой геометрии. Он родился в 1792 году в Нижнем Новгороде и умер в 1856 году в Казани.
Что такое неевклидова геометрия?
Неевклидова геометрия — это геометрия, в которой не выполняется один из постулатов Евклида, а именно, постулат о параллельных прямых. В неевклидовой геометрии существует несколько видов параллельных линий и треугольники не имеют суммы углов, равной 180 градусов.
Что значит, что в евклидовой геометрии параллельные прямые не пересекаются?
В евклидовой геометрии существует только один вид параллельных линий, и они никогда не пересекаются. Это означает, что если две прямые находятся в одной плоскости и не пересекаются, то они будут параллельными и будут бесконечно удалены друг от друга.
Есть ли пересечение параллельных прямых в неевклидовой геометрии?
Да, в неевклидовой геометрии существуют несколько разных видов параллельных линий, которые могут пересекаться в точках, бесконечно удаленных от заданной плоскости. Например, на сфере любые две прямые, непересекающиеся на данной плоскости, пересекаются в двух точках, лежащих на сфере.
Какие тексты остались после Лобачевского, связанные с параллельными прямыми?
Лобачевский оставил после себя несколько работ на тему неевклидовой геометрии, в которых рассматривались проблемы связанные с параллельными прямыми. В частности, одной из наиболее известных работ является «О представлении геометрии на плоскости», опубликованная в 1829 году, в которой Лобачевский изложил свою концепцию неевклидовой геометрии.
Какие последствия имеет отказ от постулата Евклида?
Отказ от постулата Евклида и принятие неевклидовой геометрии привело к революции в математике и философии. Это помогло понять, что геометрические построения и измерения не являются единственными возможными и что реальность может быть описана различными способами, зависящими от выбранной системы координат и модели пространства. Следствия этого открытия были чрезвычайно важными для развития физики и технологии в XX веке.
Как Лобачевский повлиял на развитие математики?
Лобачевский считается одним из основоположников неевклидовой геометрии, которая стала ключевым открытием в математике XIX века. Его работы позволили понять, что абсолютную истину в геометрии невозможно достичь, а форма геометрических объектов зависит от выбранной модели пространства. Это привело к разработке новых математических теорий и методов, которые были важны для развития физики, геометрии, технологии и многих других областей знаний.
Проблемы Евклида
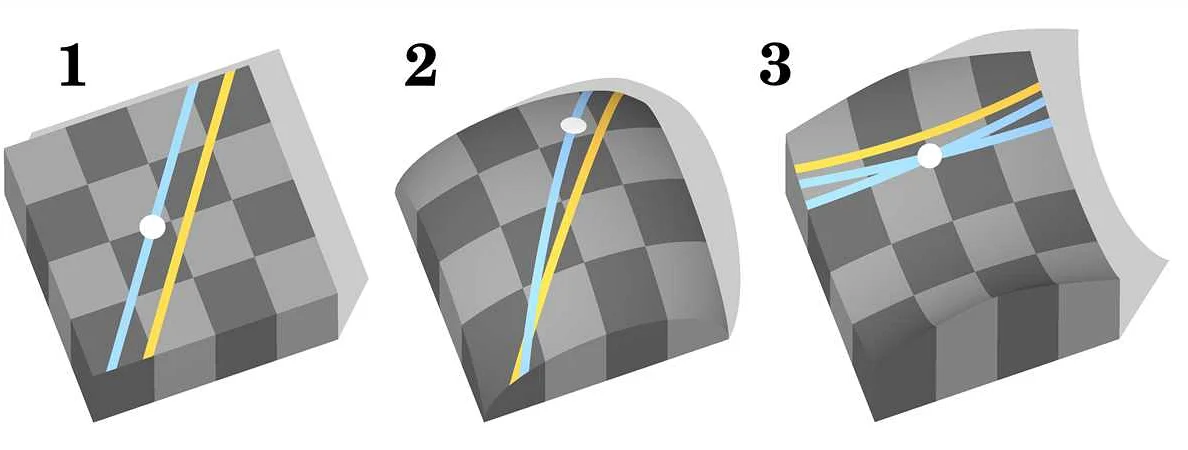
Евклид был великим древнегреческим математиком, но его работа «Начала» также является одним из наиболее известных примеров для демонстрации того, как некоторые утверждения, которые казались очевидными, могут быть ошибочными.
Проблемы Евклида были классическими проблемами в геометрии, которые были дебатированы на протяжении долгого времени. Так, например, невозможность нарисовать квадрат, который имеет площадь равную площади круга, известна как «классическая проблема квадратуры круга».
Евклид также сформулировал «проблему трёх углов», которая утверждает, что сумма углов треугольника равна 180 градусам. Он доказал это утверждение, используя свои знания о параллельных линиях, но в более общем смысле эта проблема осталась нерешенной до 19 века.
Проблемы Евклида показывают, что математика может быть сколь угодно точной и строгой, но даже в самых очевидных формулах могут быть ошибки и проблемы. Именно поэтому математики всегда стремятся искать новые доказательства и методы, которые помогут им найти ответы на вопросы, которые казались неразрешимыми.
Реформулирование аксиом геометрии
Основой ранней геометрии были аксиомы Евклида, которые были приняты как истины без доказательств. Однако, Лобачевский ввел новый способ мышления, который позволил рассматривать не единственную геометрию, а несколько.
Его новая геометрия, называемая геометрией Лобачевского, основывалась на реформулировании аксиом геометрии. Единственной и главной аксиомой стала аксиома параллельности, которая гласит что через точку, не лежащую на данной прямой, можно провести только одну параллельную данной прямой. Остальные аксиомы были пересмотрены и видоизменены.
Новые аксиомы геометрии Лобачевского стали базой для развития новых, неевклидовых геометрий. Например, Риманова геометрия представляет собой геометрию кривизны, которая нашла применение в современной физике.
Таким образом, реформулирование аксиом геометрии Лобачевским привело к возникновению новых подходов к изучению геометрии и раскрыло новые грани нашего понимания пространства и геометрии.
Геометрия Лобачевского
Геометрия Лобачевского – это геометрическая теория, основанная на работе российского математика Николая Лобачевского. Она изучает пространство, но в отличие от обычной трехмерной геометрии, Геометрия Лобачевского рассматривает пространство с кривизной, недоступной в обычной геометрии.
В Геометрии Лобачевского фундаментальным понятием является параллельность. В обычной геометрии две прямые, идущие параллельно, никогда не пересекаются. Однако в Геометрии Лобачевского это не так – казалось бы параллельные прямые могут пересекаться. Такая модель пространства называется гиперболическим пространством.
Геометрия Лобачевского имеет множество приложений в математике, физике и геодезии. Например, она используется при построении модели гравитации Леметр, при моделировании геометрических объектов на компьютере, при создании кривых Безье и др.
В итоге, Геометрия Лобачевского представляет собой интересную и важную область математики, изучающую свойства пространства с кривизной, хотя и не обычным.
Пересечение прямых на плоскости
Пересечение прямых на плоскости — важное понятие в математике, которое становится особенно интересным при рассмотрении параллельных прямых. Существует несколько случаев пересечения прямых на плоскости:
- Пересечение в точке: две прямых пересекаются в одной точке. Этот случай является самым обычным и распространенным в реальной жизни.
- Отсутствие пересечения: две прямые не имеют общих точек на плоскости.
- Совпадение прямых: две прямые совпадают, то есть имеют бесконечное число общих точек.
Если же рассматривать параллельные прямые на плоскости, то случай их пересечения не возможен. Параллельные прямые не будут иметь общих точек, кроме «бесконечно удаленных» точек, которые находятся за пределами рассматриваемой плоскости.
Именно этот факт стал предметом исследования для русского математика Лобачевского, который разработал неевклидову геометрию. Он показал, что параллельные прямые на плоскости могут иметь общее пересечение на бесконечности, что нарушает аксиому Евклида о параллельных прямых.
Понимание пересечения прямых на плоскости является важным для различных областей науки и техники. Например, в компьютерной графике и визуализации, геометрия играет большую роль в создании реалистичных изображений.
Линии и поверхности Лобачевского
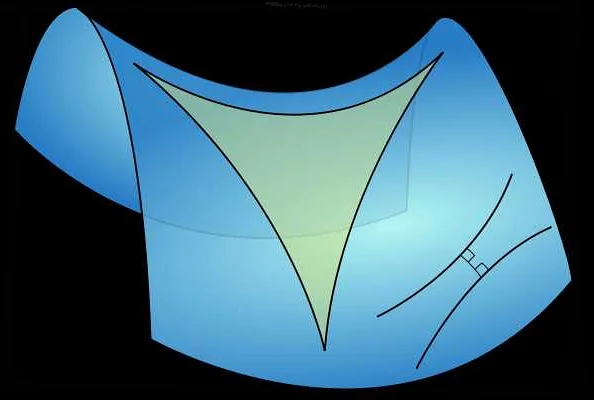
Николай Иванович Лобачевский – математик, который создал геометрию, отличную от евклидовой геометрии, называемую геометрией Лобачевского. В этой геометрии принцип параллельности не сохраняется, и нет определенного пересечения параллельных прямых. Вместо этого, параллельные линии расходятся в бесконечность.
В геометрии Лобачевского существуют различные типы линий и поверхностей, которые основаны на идеи неевклидовой геометрии. Одна из таких линий – геодезическая, которая является аналогом прямой в евклидовой геометрии. Геодезические линии Лобачевского имеют свойства, которые противоположны свойствам евклидовских прямых. Вместо того, чтобы быть одной, прямой, геодезическая линия Лобачевского может определяться как круг в гиперболической плоскости.
В геометрии Лобачевского также существуют поверхности, которые представляют собой аналоги плоскостей в евклидовой геометрии. Гиперболические поверхности Лобачевского имеют свойства, которые отличаются от свойств евклидовых плоскостей. Например, на гиперболической поверхности площадь треугольника суммируется меньше, чем на евклидовой плоскости.
Таким образом, геометрия Лобачевского представляет собой довольно непривычный мир, где принципы элементарной геометрии не действуют. Однако, эта геометрия имеет огромное значение в математике и физике, и применяется в различных областях науки.
Перспектива применения геометрии Лобачевского
Геометрия Лобачевского нашла свое применение в различных областях науки и техники. Например, она находит применение в геодезии, при создании геодезических сетей. Также она полезна в компьютерной графике и архитектуре при создании трехмерных моделей объектов и ландшафтов.
В области теории игр геометрия Лобачевского тесно связана с теорией выбора. Она позволяет рассчитывать рациональные и оптимальные стратегии в различных играх. Также она нашла применение в криптографии, например, при создании безопасных криптографических алгоритмов.
Кроме того, геометрия Лобачевского имеет большое значение в фундаментальной математике. Она позволила пересмотреть и расширить классическую геометрию Евклида, открыв двери для развития новых математических дисциплин, таких как топология или геометрия Римана.
Таким образом, геометрия Лобачевского — это не только теория, разработанная одним математиком, но и широкое поле для исследований и разработок в различных областях науки и техники.
Различия между геометрией Лобачевского и классической геометрией
1. Количество параллельных прямых
В классической геометрии существует только одна прямая, проходящая через заданную точку, и параллельная данной прямой. Однако, в геометрии Лобачевского существует бесконечное количество параллельных прямых, проходящих через заданную точку.
2. Углы
В классической геометрии сумма углов треугольника равна 180 градусов. В геометрии Лобачевского сумма углов треугольника меньше 180 градусов.
3. Длины искривленных линий
В классической геометрии длина окружности вычисляется по формуле C=2πr, где r — радиус окружности. В геометрии Лобачевского окружность является плоским гиперболоидом, поэтому для вычисления ее длины нужно использовать специальный интеграл.
4. Площадь фигур
В классической геометрии площадь фигуры вычисляется по формуле S=ab, где a и b — стороны прямоугольника, равного данной фигуре. В геометрии Лобачевского площадь фигуры вычисляется по формуле S=αR^2, где α — некоторая константа, зависящая от типа фигуры, а R — радиус некоторого круга, лежащего на плоскости, на которой находится фигура.
5. Аксиомы
Классическая геометрия основана на пяти аксиомах, сформулированных Евклидом. В геометрии Лобачевского одна из этих аксиом не выполняется — это аксиома параллельности.
Применение геометрии Лобачевского в современных науках

Геометрия Лобачевского – это необычайно интересная и популярная модель геометрии, которая нашла свое применение в различных областях науки. Созданная Николаем Лобачевским в XIX веке, она дает возможность рассматривать геометрические пространства, отличные от стандартных Евклидовых трехмерных пространств.
Одним из применений геометрии Лобачевского является теория относительности Альберта Эйнштейна, в которой основу составляют неевклидовы пространства. Большое значение геометрия Лобачевского имеет также в математическом анализе, теории вероятностей и теории информации. Геометрические модели Лобачевского нашли применение в конструировании ударопрочных стекол, а также в некоторых областях компьютерной графики и видеосъемки.
Безусловно, геометрия Лобачевского является актуальной для современных наук и находит все больше применений. Эта непривычная геометрическая модель дает возможность расширить понимание пространства и применить ее в практических вопросах.
- Применение геометрии Лобачевского в теории относительности
- Использование геометрии Лобачевского в математическом анализе
- Геометрия Лобачевского в конструировании ударопрочных стекол
- Геометрические модели Лобачевского в области компьютерной графики и видеосъемки
Таким образом, геометрия Лобачевского является одной из важнейших моделей геометрии, нашедшей свое применение в различных областях современных наук. Без ее использования невозможно было бы рассмотреть нетривиальные геометрические пространства и решать многие практические задачи.
Выводы

Изучение творчества Николая Ивановича Лобачевского, позволяет сделать следующие выводы:
- Лобачевский был выдающимся ученым-математиком, чьи заслуги очень высоко ценятся сейчас и были невероятно важны для развития математики в конце XIX и начале XX столетия.
- Парадокс Лобачевского о параллельных прямых стал частью математической теории неевклидовой геометрии, которая стала фундаментом для развития не только математики, но и физики и космологии.
- Работы Лобачевского перевернули устоявшиеся представления о геометрии и математике в целом, изменив понимание мира и способность понимать его законы.
- Лобачевский был гением своего времени, который смог, используя свой ум и научную находчивость, прийти к принципиально новым результатам и создать новый раздел математики.
Таким образом, творчество Лобачевского очень важно для истории математики, философии и науки в целом, и его достижения остаются актуальными и значимыми в наши дни.