Что такое математике модели

Математические модели — это абстрактные конструкции, которые используются для описания и предсказания реальных явлений и процессов с помощью математических методов. Они являются важным инструментом в науке, экономике, инженерии и других областях, позволяя исследователям анализировать сложные системы, прогнозировать результаты и принимать обоснованные решения. В этой статье мы рассмотрим основные принципы создания математических моделей и их роль в различных областях человеческой деятельности.

Математическая модель — это абстрактное представление какого-либо реального процесса, системы или явления при помощи математических символов и формул. Она позволяет описывать, анализировать и предсказывать поведение объектов и явлений в различных ситуациях. Математические модели широко применяются в науке, инженерии, экономике, социологии и других областях.

Математическая модель может быть дискретной или непрерывной, статической или динамической. Дискретная модель описывает объекты или процессы, которые принимают определенные значения или состояния в определенные моменты времени. Непрерывная модель, в свою очередь, описывает процессы, которые изменяются плавно и непрерывно во времени или пространстве.

Разработка математической модели включает в себя несколько этапов. Сначала необходимо определить цель моделирования и выбрать соответствующие математические методы и инструменты. Затем происходит математическое описание объекта или явления, выделение основных переменных и установление связей между ними. После этого проводятся вычисления, анализ полученных результатов и проведение экспериментов для проверки модели на реальных данных.

Математическая модель позволяет сократить время и затраты на проведение реальных экспериментов и исследований, а также предоставляет возможность исследовать объекты и явления, которые невозможно наблюдать или измерить напрямую. Она помогает улучшить понимание и предсказание поведения реальных систем, а также разрабатывать оптимальные стратегии и решения в различных областях деятельности.

Математическая модель может быть использована для решения различных задач, таких как оптимизация процессов, прогнозирование будущих событий, анализ и сравнение различных вариантов решений. Она позволяет ученому или инженеру увидеть «внутреннюю картину» объекта или явления, выявить его сильные и слабые стороны, а также предложить способы улучшения и оптимизации.

Понятие математической модели

Математическая модель позволяет представить сложные явления в виде формальной системы, которую можно изучать и анализировать. Она упрощает сложные задачи и позволяет решать их с помощью математических методов.

Математическая модель может быть использована для прогнозирования, оптимизации, анализа и планирования различных процессов и систем. Она помогает понять взаимосвязь различных переменных и факторов, а также предсказать поведение системы в различных условиях.

Важными характеристиками математической модели являются ее точность, адекватность и применимость. Она должна быть достаточно точной, чтобы отражать реальные явления или процессы, а также адекватной – чтобы учитывать все существенные факторы и переменные. Кроме того, модель должна быть применимой – чтобы можно было решать практические задачи с ее помощью.

Математические модели широко используются в различных областях, таких как физика, экономика, биология, социология и др. Они являются важным инструментом для исследований, предсказаний и принятия решений.

Какие задачи решает математическая модель?

Математическая модель позволяет решать широкий спектр задач в различных областях, включая физику, экономику, биологию, социологию и технику. Она может использоваться для:

• Прогнозирования и предсказания поведения объекта или явления.
• Оптимизации и поиска наилучших решений.
• Анализа и сравнения различных вариантов или стратегий.
• Изучения влияния различных факторов или параметров на систему.
• Моделирования и симуляции реальных процессов или систем.

Математическая модель может быть представлена в виде уравнений, систем уравнений, графов, статистических распределений и других математических объектов. Она позволяет формализовать и анализировать сложные явления и процессы, которые не всегда могут быть описаны с помощью естественного языка.

Использование математических моделей позволяет сократить время и ресурсы, которые требуются для решения сложных задач. Они позволяют проводить исследования, тестирования и оптимизации в виртуальной среде, что может быть намного более безопасным и экономически выгодным, чем проведение экспериментов на реальных объектах или системах.

Принципы работы математической модели

Математическая модель представляет собой формализованное описание реальной системы или явления с использованием математических методов и понятий. Она позволяет анализировать и прогнозировать поведение системы, оптимизировать ее работу и принимать решения.

Принципы работы математической модели включают следующие этапы:

1. Определение целей моделирования. На этом этапе определяются основные вопросы, на которые требуется получить ответы с помощью модели. Четкое определение целей позволяет сосредоточиться на ключевых аспектах моделирования и выбрать наиболее подходящие математические методы.
2. Сбор данных. Для построения математической модели необходимо обладать надежной и достаточной информацией о системе или явлении. Данные могут быть получены из источников, проведены эксперименты или использованы результаты предыдущих исследований. Сбор данных должен быть проведен с учетом требований моделирования и статистических методов обработки информации.
3. Выбор математических методов. На этом этапе определяются математические модели и методы, которые будут использоваться для описания системы или явления. Выбор зависит от типа модели, доступных данных и целей моделирования. Различные методы включают в себя статистические модели, дифференциальные уравнения, оптимизацию и другие.
4. Разработка модели. На этом этапе строится математическая модель на основе выбранных методов. Модель должна учитывать все существенные факторы и взаимосвязи, которые влияют на систему или явление. Разработка модели может быть сложным процессом, требующим математических расчетов, программирования и проверки на корректность.
5. Проверка и анализ модели. После построения модели необходимо ее проверить и проанализировать. Это включает в себя сравнение результатов моделирования с реальными данными или наблюдениями, а также анализ чувствительности модели к изменениям входных параметров. Если модель не соответствует требованиям, она может быть модифицирована или заменена другой моделью.
6. Применение модели. Последний этап заключается в использовании математической модели для решения конкретных задач или прогнозирования будущих событий. Модель может быть использована для оптимизации работы системы, прогнозирования результатов и принятия решений. Важно учитывать ограничения модели и возможные ошибки при ее использовании.

Принципы работы математической модели позволяют ученным, инженерам и другим специалистам в различных областях применять аналитические подходы для более глубокого понимания и управления сложными системами и явлениями.

Компоненты математической модели

Математическая модель представляет собой абстракцию реального явления или процесса, которую можно описать с помощью математических уравнений и формул. Она состоит из нескольких компонентов, каждый из которых выполняет определенную роль в описании моделируемого явления.

1. Переменные: Математическая модель содержит переменные, которые представляют собой величины, зависящие от времени или других параметров. Эти переменные могут быть измеримыми или неизмеримыми и представлять различные характеристики моделируемого объекта или процесса.
2. Параметры: Параметры математической модели определяют ее основные свойства и характеристики. Они могут быть константами или функциями времени и могут влиять на поведение модели и ее решение. Параметры модели могут быть определены с помощью экспериментов, наблюдений или теоретических предположений.
3. Уравнения: Математическая модель описывается системой математических уравнений, которые связывают переменные и параметры модели. Эти уравнения могут быть дифференциальными, алгебраическими или их комбинацией. Уравнения модели позволяют предсказывать изменение значения переменных во времени или в зависимости от других параметров.
4. Граничные условия: Граничные условия определяют значения переменных или их производных на границах модельной области или на определенных границах времени. Эти условия могут быть заданы экспериментально или теоретически и являются важной частью математической модели. Они ограничивают поведение модели и позволяют решать уравнения с учетом этих ограничений.
5. Начальные условия: Начальные условия определяют значения переменных или их производных в начальный момент времени или в начальной точке модельной области. Они могут быть заданы экспериментально или теоретически и также являются важной частью математической модели. Начальные условия позволяют решать дифференциальные уравнения и найти значения переменных в любой момент времени или в любой точке модельной области.

Компоненты математической модели взаимодействуют друг с другом, образуя систему уравнений, которые могут быть решены численными или аналитическими методами. Решение математической модели позволяет предсказать поведение моделируемого явления, оптимизировать параметры модели или принять решения на основе полученных результатов.

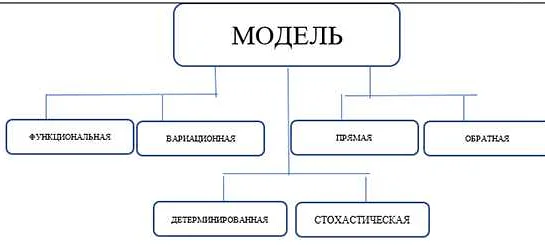
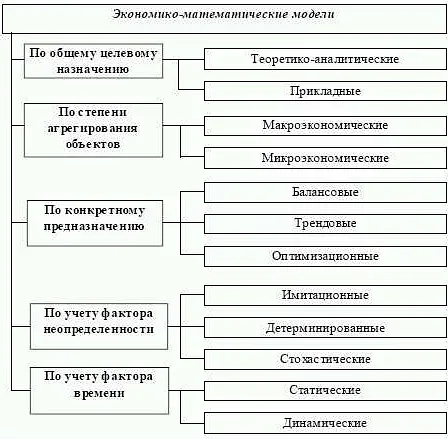
Виды математических моделей

Математические модели могут быть разделены на несколько типов в зависимости от того, как они описывают конкретные явления или системы. Ниже перечислены основные виды математических моделей:

1. Аналитические модели — это модели, которые могут быть выражены с помощью аналитических формул или уравнений. Они обычно используются для описания математических законов или физических принципов. Примерами аналитических моделей являются уравнения Ньютона в физике или уравнения Максвелла в электродинамике.
2. Статистические модели — это модели, которые используются для анализа статистических данных и предсказания вероятностных распределений. Они часто используются в экономике, социологии и других областях, где данные не всегда точны или полны. Примерами статистических моделей являются регрессионные модели и модели временных рядов.
3. Дискретные модели — это модели, которые описывают системы или явления с конечным или счетным числом состояний. Они часто используются в теории игр, теории очередей и теории автоматов. Примерами дискретных моделей являются игры в кости, модели марковских цепей и автоматы Тьюринга.
4. Непрерывные модели — это модели, которые описывают системы или явления с непрерывными переменными. Они используются в физике, инженерии и других областях, где переменные могут принимать любое значение в определенном диапазоне. Примерами непрерывных моделей являются уравнения теплопроводности и уравнения Навье-Стокса в гидродинамике.
5. Геометрические модели — это модели, которые используют геометрические принципы и формы для описания систем или явлений. Они часто применяются в компьютерной графике, дизайне и архитектуре. Примерами геометрических моделей являются трехмерные модели объектов или моделирование поверхностей.

Каждый тип модели имеет свои особенности и применение в различных областях науки и техники. Выбор конкретного типа модели зависит от целей и требований исследования или проекта.

Примеры применения математических моделей

Физика:

Математические модели используются в физике для описания различных физических явлений. Например, модель движения тела под действием гравитации позволяет предсказать его траекторию и скорость.

Экономика:

В экономике математические модели применяются для анализа и прогнозирования различных экономических процессов, таких как инфляция, валютные курсы и рост национального дохода.

Биология:

Математические модели используются в биологии для изучения различных биологических систем, таких как популяции животных или распространение болезней. Эти модели позволяют предсказать изменения в популяции или распространение болезней в зависимости от различных факторов.

Технические науки:

В технических науках математические модели применяются для проектирования и оптимизации различных систем, например, электрических цепей или механических конструкций. Они позволяют предсказать поведение системы и оптимизировать ее параметры.

Климатология:

В климатологии математические модели используются для изучения климатических изменений и прогнозирования будущих погодных условий. Они учитывают различные факторы, такие как солнечная радиация, атмосферные условия и океанические течения.

Социальные науки:

В социальных науках математические модели применяются для анализа социальных систем и прогнозирования их поведения. Например, моделируются социальные сети, распространение информации или формирование общественного мнения.

Эти примеры только небольшая часть областей, где математические модели находят свое применение. В каждой из них модели играют важную роль в анализе данных и прогнозировании результатов.

Ограничения и проблемы математических моделей

• Упрощение действительности: Математические модели обычно основываются на предположениях и упрощениях, чтобы сделать проблему более управляемой и понятной. Однако в реальном мире могут существовать множество факторов и взаимодействий, которые не учитываются моделью.
• Неполные данные: Часто бывает сложно получить полные и точные данные для построения математической модели. Недостаток информации может привести к неточным результатам или невозможности создания модели вообще.
• Сложность модели: Некоторые явления или системы могут быть настолько сложными, что создание математической модели становится сложной задачей. Это может быть вызвано высокой степенью нелинейности, случайностью или взаимодействиями множества переменных.
• Неясность параметров: В некоторых случаях может быть сложно определить значения параметров модели. Например, при моделировании экономических явлений может быть неясно, как оценить величину спроса или предложения.
• Чувствительность к начальным условиям: Многие математические модели являются чувствительными к начальным условиям. Это значит, что малые изменения входных данных могут привести к значительным изменениям результатов.
• Ограниченность предсказаний: Хотя математические модели могут помочь предсказать поведение системы в определенном диапазоне условий, они часто неспособны предсказывать долгосрочное поведение или реакцию на экстремальные условия.

Несмотря на эти ограничения и проблемы, математические модели по-прежнему являются ценным инструментом для науки, инженерии, экономики и других областей. Они позволяют ученым и исследователям лучше понимать и анализировать сложные системы, а также принимать обоснованные решения на основе предсказаний моделей.

Вопрос-ответ:

Что такое математическая модель?

Математическая модель — это абстрактная структура, созданная для описания и исследования реальных явлений с помощью математических методов и формул.

Как работает математическая модель?

Математическая модель работает путем представления реального объекта или процесса в виде математических уравнений и формул. Затем, используя эти уравнения, можно проводить различные вычисления и анализировать поведение модели в различных ситуациях.

Какие примеры математических моделей существуют?

Существует множество примеров математических моделей, которые применяются в различных областях. Например, модели научного прогнозирования, модели экономических процессов, модели климата, модели трафика и т.д.

Зачем нужны математические модели?

Математические модели позволяют упростить сложные реальные системы и процессы, выделить основные закономерности и прогнозировать их поведение в различных ситуациях. Они также позволяют проводить эксперименты и тестирование гипотез без необходимости непосредственного взаимодействия с реальными объектами или процессами.

Какие ограничения есть у математических моделей?

Одним из основных ограничений математических моделей является их абстрактность и упрощенность. Математическая модель не может полностью учесть все детали и особенности реального объекта или процесса. Также важно, чтобы модель была достаточно точной, чтобы давать адекватные результаты.

Что такое математическая модель?

Математическая модель — это абстрактная математическая структура, которая описывает определенную систему, процесс или явление в виде формул, уравнений или алгоритмов.

Видео по теме: