Что такое аргумент в математике

Аргумент в математике – это значение, которое подставляется в функцию или операцию для получения определенного результата. Аргумент может быть числом, переменной или выражением, которое задает условия для выполнения операции. В математике, аргументы играют важную роль в определении значений функций и решении уравнений и задач. Умение правильно определить и использовать аргументы помогает улучшить понимание и применение математических концепций.

Аргумент — это величина, которая определяет положение точки на плоскости или в пространстве. В математике аргумент обычно измеряется в градусах или радианах и используется для описания угла, который образуют вектор или сторона многоугольника с определенной осью или направлением.

Аргумент может принимать значения от 0 до 360 градусов или от 0 до 2π радиан. Например, если точка находится на положительной оси x, то ее аргумент равен 0 градусов или 0 радиан. Если точка находится на отрицательной оси x, то ее аргумент равен 180 градусов или π радиан.

Пример: Рассмотрим точку с координатами (3, 4) на плоскости. Чтобы найти аргумент этой точки, можно воспользоваться теоремой Пифагора и формулой tg(α) = противолежащий/противлежащий. В данном случае противолежащий равен 4, а прилежащий равен 3. Таким образом, tg(α) = 4/3. Находим α, используя функцию арктангенс: α = arctan(4/3). Ответ: α ≈ 53.13 градусов или π/3 радиан.

Аргументы широко применяются в различных областях математики, физики, инженерии и компьютерных наук. Они позволяют описывать положение и направление объектов, рассчитывать траектории движения, моделировать волновые процессы и многое другое. Понимание аргумента важно для решения задач, связанных с геометрией, тригонометрией, комплексными числами и другими областями математики.

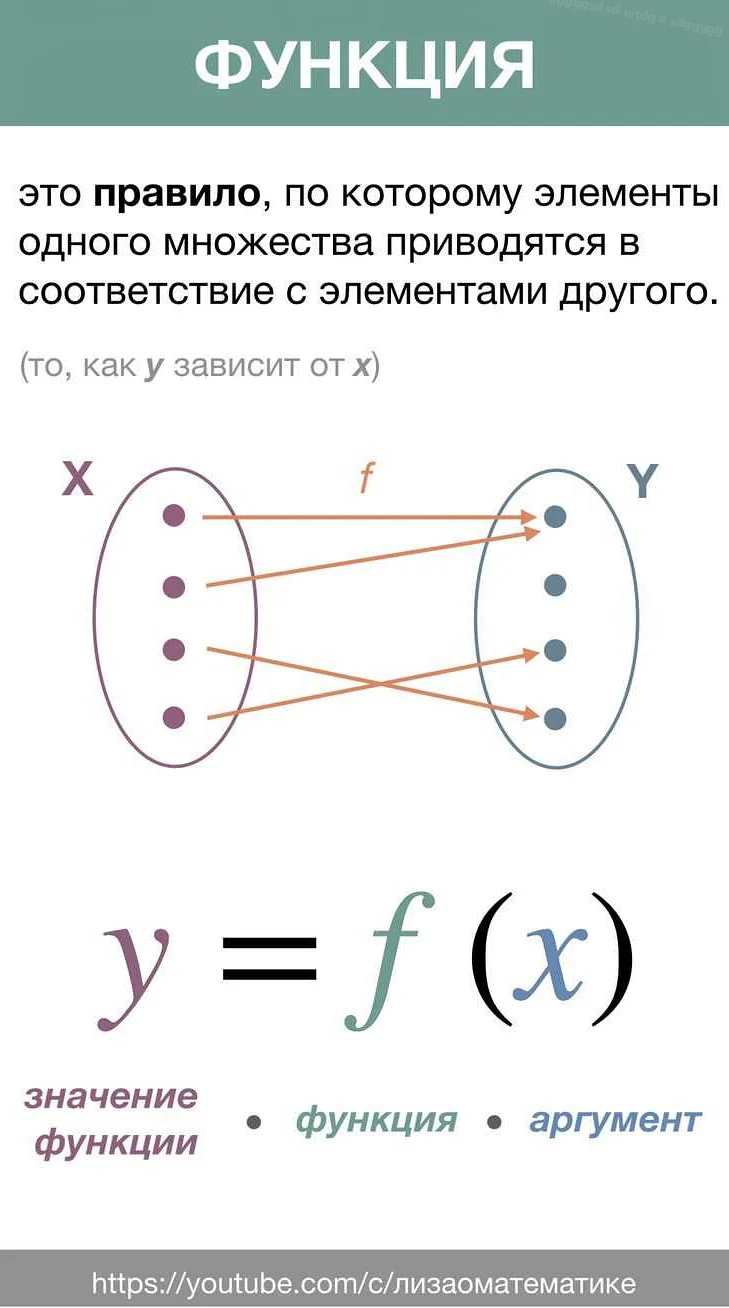
Определение понятия «аргумент»

Аргумент является одним из ключевых понятий в математике, поскольку он определяет, какие значения будут передаваться в функцию и какие результаты она будет возвращать.

Аргумент может быть числом, переменной или выражением. Например, в функции f(x) = x^2 переменная x является аргументом. Если передать в нее значение 2, то результатом будет 4.

Аргументы могут также использоваться для определения диапазона значений, в котором функция определена. Например, в функции g(x) = sqrt(x) аргумент x должен быть неотрицательным числом, поскольку иначе результатом будет комплексное число.

В математике аргументы могут также использоваться для определения условий или ограничений, которые должны выполняться. Например, в функции h(x) = log(x) аргумент x должен быть положительным числом, поскольку иначе результатом будет неопределенное значение.

ПримерЗначение аргументаРезультат

f(x) = x^2	2	4
g(x) = sqrt(x)	4	2
h(x) = log(x)	1	0

Роль аргумента в математике

В тригонометрии аргументом является угол, который определяет положение точки на окружности. Значение синуса, косинуса или других тригонометрических функций зависит от значения аргумента. Например, для угла 45 градусов аргументом будет π/4 радиан. Знание аргумента позволяет определить значение тригонометрической функции.

В комплексном анализе аргументом комплексного числа является угол, который образует данное число с положительным направлением оси действительных чисел. Аргумент комплексного числа важен при выполнении операций с ним, таких как умножение и деление. Например, умножение двух комплексных чисел сводится к умножению их модулей и сложению их аргументов.

Аргумент также играет важную роль в логарифмах и экспонентах. В этом контексте аргументом является число, возведенное в степень или взятое под логарифм. Знание аргумента позволяет определить значение функции.

В общем смысле, аргумент представляет собой независимую переменную, которая влияет на результат математической операции или функции. Знание аргумента позволяет определить и предсказать значения функций и операций в различных математических дисциплинах.

Аргумент в функциях

Аргументы в функциях могут быть различных типов, например, числами, строками, списками и т. д. В зависимости от определения функции, количество аргументов может быть разным – от одного до нескольких.

Аргументы могут быть обязательными или необязательными. Обязательные аргументы обязательно должны быть переданы в функцию при ее вызове, иначе будет ошибка. Необязательные аргументы могут иметь значения по умолчанию, которые будут использоваться, если аргумент не был передан при вызове функции.

Примером функции с обязательными аргументами может быть функция вычисления площади прямоугольника. Она принимает два аргумента: длину и ширину прямоугольника. Если не передать значения этих аргументов, функция не сможет вычислить площадь и выдаст ошибку.

Примером функции с необязательными аргументами может быть функция приветствия. Она принимает один аргумент – имя человека. Если имя не будет передано, функция будет использовать значение по умолчанию и приветствовать «гостя».

Таким образом, аргументы в функциях играют важную роль, определяя поведение функции и ее результаты.

Аргумент в комплексных числах

Аргумент обычно измеряется в радианах, но также может быть выражен в градусах. Диапазон аргумента обычно ограничен от 0 до 2π радиан или от 0 до 360 градусов.

Для комплексного числа z = a + bi, где a — действительная часть числа, b — мнимая часть числа, аргумент можно вычислить с помощью следующей формулы:

арг(z) = atan(b/a), если a > 0;

арг(z) = atan(b/a) + π, если a < 0 и b ≥ 0;

арг(z) = atan(b/a) — π, если a < 0 и b < 0;

арг(z) = π/2, если a = 0 и b > 0;

арг(z) = -π/2, если a = 0 и b < 0;

Здесь atan — обратная тангенс функция, возвращающая значение угла от -π/2 до π/2 радиан.

Знание аргумента комплексного числа позволяет найти его модуль и экспоненциальную форму записи.

Например, для комплексного числа z = 1 + i:

арг(z) = atan(1/1) = π/4 радиан (или 45 градусов).

Примеры использования аргумента в математике

Аргумент в математике используется для обозначения значения, при котором функция принимает определенное значение или удовлетворяет определенным условиям. Рассмотрим несколько примеров использования аргумента в математике:

1. Аргумент в тригонометрии: в тригонометрии аргументом функции является угол, выраженный в радианах или градусах. Например, в функции синуса sin(x), аргументом является угол x, который может быть задан в радианах или градусах.

2. Аргумент в логарифмической функции: в логарифмической функции log(x), аргументом является число x, для которого ищется логарифм. Например, в функции log(100), аргументом является число 100, для которого мы хотим найти логарифм.

3. Аргумент в функции экспоненты: в функции экспоненты exp(x), аргументом является число x, на которое возводится основание экспоненты (обычно число e). Например, в функции exp(2), аргументом является число 2, которое возводится в степень основания экспоненты.

4. Аргумент в квадратном уравнении: в квадратном уравнении ax^2 + bx + c = 0, аргументом является переменная x, которую мы ищем. Например, в уравнении 2x^2 + 5x — 3 = 0, аргументом является переменная x, которая должна удовлетворять уравнению.

Таким образом, аргумент в математике играет важную роль в определении и решении различных функций и уравнений. Он помогает нам определить значения функций при заданных условиях и найти решения уравнений.

Как найти аргумент числа

Для нахождения аргумента числа необходимо выполнить следующие шаги:

1. Представить число в виде комплексного числа вида z = a + bi, где a — действительная часть, b — мнимая часть.
2. Вычислить модуль числа z по формуле |z| = √(a^2 + b^2), где a^2 — квадрат действительной части, b^2 — квадрат мнимой части.
3. Вычислить аргумент числа z по формуле arg(z) = arctan(b/a), где arctan — арктангенс, b/a — отношение между мнимой и действительной частями числа.

В результате выполнения этих шагов мы получаем аргумент числа, выраженный в радианах. Чтобы получить аргумент в градусах, можно воспользоваться формулой: аргумент в градусах = аргумент в радианах * (180/π), где π — число Пи.

Например, если дано комплексное число z = 3 + 4i, то его аргумент можно найти следующим образом:

Модуль числа z = √(3^2 + 4^2) = √(9 + 16) = √25 = 5

Аргумент числа z = arctan(4/3) ≈ 0.93 радиан ≈ 53.13 градусов

Таким образом, аргумент числа z ≈ 53.13 градусов.

Свойства аргумента

1. Уникальность: каждому комплексному числу соответствует единственный аргумент. Это означает, что у разных комплексных чисел не может быть одинаковых аргументов.

2. Множественность: каждому комплексному числу соответствует бесконечное множество аргументов, отличающихся друг от друга на целое кратное 2π. Например, если аргумент одного комплексного числа равен π/4, то его множество аргументов будет содержать все числа вида π/4 + 2πk, где k — целое число.

3. Геометрическая интерпретация: аргумент комплексного числа определяет угол между положительным направлением оси действительных чисел и лучом, соединяющим начало координат и точку, соответствующую комплексному числу на комплексной плоскости.

4. Сложение аргументов: аргументы комплексных чисел можно складывать. Если у двух комплексных чисел аргументы равны α и β, то аргумент их суммы будет равен α + β.

5. Умножение аргументов: аргументы комплексных чисел можно умножать. Если у двух комплексных чисел аргументы равны α и β, то аргумент их произведения будет равен α + β.

Знание свойств аргумента позволяет более глубоко понять и использовать комплексные числа в математике и других науках.

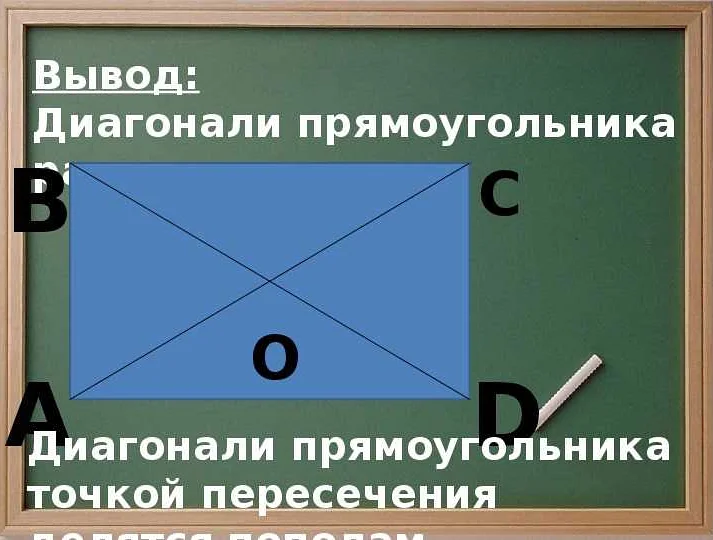
Значение аргумента в геометрии

Аргумент широко используется при описании положения точек на плоскости или в пространстве. Например, в полярной системе координат, аргумент определяет направление радиус-вектора от начала координат к точке. В трехмерной геометрии, аргумент может использоваться для указания угла поворота вокруг оси.

Значение аргумента может быть выражено как число, соответствующее углу, или как выражение с переменными. Например, в случае окружности, аргументом точки на окружности может быть угол, измеренный от положительного направления оси абсцисс до луча, проведенного от начала координат к точке.

В геометрии аргумент также используется для определения понятий пересечения и симметрии фигур. Например, при определении пересечения двух окружностей или пересечения прямой с плоскостью, аргументы углов могут использоваться для определения точки пересечения.

Вопрос-ответ:

Что такое аргумент в математике?

Аргумент в математике — это значение, которое подставляется в функцию или операцию для получения результата. В более простых словах, аргумент — это то, что мы «подаём на вход» в математическое выражение.

Можете привести пример аргумента в математике?

Конечно! Рассмотрим пример функции y = 2x — 3. Здесь аргументом функции является переменная «x». Если мы подставим вместо «x» значение, например, 5, то получим следующее выражение: y = 2 * 5 — 3 = 7. Таким образом, аргументом в этом случае будет число 5.

Какие еще примеры аргументов можно привести?

В математике аргументами могут быть не только числа, но и различные переменные, выражения или даже другие функции. Например, в функции y = sin(x), аргументом является переменная «x». Также можно рассмотреть пример выражения (a + b) * c, где аргументами будут выражения (a + b) и «c».

Какова роль аргумента в математических операциях?

Аргументы играют важную роль в математических операциях, так как именно через них мы задаем условия или значения для выполнения операции. Аргументы позволяют нам изменять входные данные и получать разные результаты при выполнении одних и тех же операций.

Может ли аргумент принимать отрицательные значения?

Да, аргументы могут принимать отрицательные значения. Например, в функции y = x^2, аргументом «x» может быть и отрицательное число, и положительное число. В зависимости от значения аргумента, мы получим разные значения функции.

Что такое аргумент в математике?

Аргумент в математике — это значение, которое подставляется в функцию для вычисления соответствующего значения функции. Он является независимой переменной, которая влияет на значение функции. Например, в функции f(x) = 2x, аргументом является x, который может принимать различные значения.

Видео по теме: