Что такое диагональ многоугольника 4 класс математика

Диагональ многоугольника 4 класс математика – это отрезок, соединяющий две вершины многоугольника, не являющиеся соседними. Узнайте, как найти длину диагонали многоугольника и узнайте, как применить это понятие в математике для решения задач.

Диагональ многоугольника – это отрезок, который соединяет две вершины многоугольника, не являющиеся соседними. Она проходит внутри многоугольника и делит его на два треугольника или несколько треугольников, в зависимости от количества его вершин. Диагональ является важным понятием в геометрии и используется для решения различных задач.

Например, если у нас есть пятиугольник, то у него будет две диагонали – одна, которая соединяет первую вершину с третьей, и вторая, соединяющая вторую и четвертую вершины. Диагонали помогают разбить многоугольник на более простые фигуры, что может быть полезно при решении задач на вычисление площади или поиска углов.

Использование диагоналей предоставляет дополнительные возможности для анализа и изучения многоугольников. Например, можно установить, что сумма углов в треугольнике, соседнем к одной из диагоналей, равна 180 градусам. Это позволяет использовать диагонали для нахождения значений углов в многоугольниках.

Что такое диагональ многоугольника?

Диагонали многоугольника играют важную роль в геометрии. Они помогают определить различные характеристики многоугольника, такие как количество диагоналей, сумма углов, число треугольников, образованных диагоналями и другие свойства.

Диагонали многоугольника могут быть равными или неравными. Например, в треугольнике все три стороны являются диагоналями, потому что все вершины несоседние. В квадрате есть две диагонали, которые являются равными сторонам квадрата.

Диагонали многоугольника могут пересекаться внутри или снаружи самого многоугольника. Количество пересечений диагоналей определяет, насколько сложной будет форма многоугольника.

Диагонали многоугольника используются в различных областях, включая архитектуру, графику, компьютерные игры и другие приложения. Знание о диагоналях многоугольника помогает в решении геометрических задач и построении различных фигур.

Видео по теме:

Понятие диагонали многоугольника

Внутренние диагонали — это отрезки, которые лежат полностью внутри многоугольника.

Внешние диагонали — это отрезки, которые соединяют вершину многоугольника с вершиной, не являющейся его соседней, и лежат вне многоугольника.

Диагонали многоугольника имеют ряд свойств:

1. В многоугольнике с n вершинами количество диагоналей равно n * (n-3) / 2.
2. Все диагонали многоугольника равны между собой по длине, если многоугольник равнобедренный.
3. Все диагонали многоугольника равны между собой по длине и равны радиусу описанной окружности, если многоугольник равносторонний.

Знание о диагоналях многоугольника позволяет решать задачи связанные с его свойствами и конструкциями.

Свойства диагоналей многоугольника

1. Количество диагоналей

Количество диагоналей в многоугольнике можно найти по формуле: D = (n × (n-3)) / 2, где D — количество диагоналей, а n — количество вершин многоугольника. Например, в треугольнике (n=3) нет диагоналей, в четырехугольнике (n=4) есть две диагонали, в пятиугольнике (n=5) — пять диагоналей.

2. Взаимное расположение диагоналей

Диагонали многоугольника могут пересекаться или не пересекаться. Если диагонали пересекаются внутри многоугольника, то они делят фигуру на треугольники. Если диагонали не пересекаются, то многоугольник делится на четырехугольники.

3. Свойства диагоналей

Диагонали многоугольника могут быть разной длины. Однако в выпуклых многоугольниках самая длинная диагональ соединяет самые удаленные вершины. Кроме того, сумма длин всех диагоналей выпуклого многоугольника равна произведению количества вершин на количество вершин минус 3, деленное на 2.

Например, в пятиугольнике (n=5) самая длинная диагональ соединяет первую и третью вершину, а сумма длин всех диагоналей равна (5 × (5-3)) / 2 = 5.

Таким образом, диагонали многоугольника имеют свои особенности и свойства, которые помогают лучше понять и изучить структуру этой геометрической фигуры.

Примеры диагоналей многоугольников

Рассмотрим несколько примеров диагоналей многоугольников:

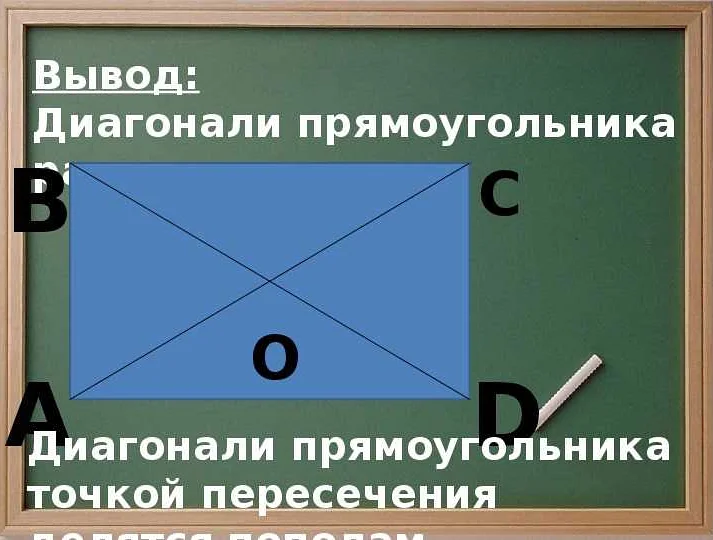
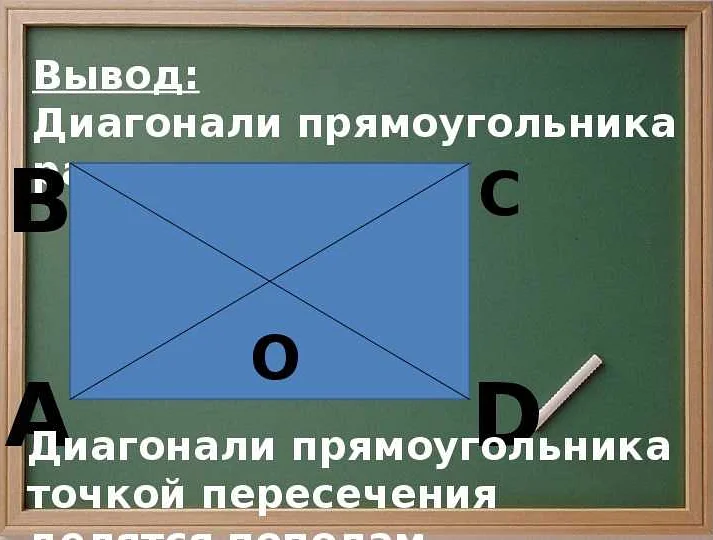
Прямоугольник:

Прямоугольник имеет четыре вершины. Диагонали прямоугольника соединяют противоположные вершины и пересекаются в центре прямоугольника. Таким образом, прямоугольник имеет две диагонали.

Равносторонний треугольник:

Равносторонний треугольник имеет три вершины, все стороны имеют одинаковую длину. Диагонали равностороннего треугольника проходят через его центр и делят его на три равных треугольника. Таким образом, равносторонний треугольник имеет три диагонали.

Пятиугольник:

Пятиугольник имеет пять вершин. Диагонали пятиугольника соединяют несоседние вершины и образуют пять треугольников внутри пятиугольника. Таким образом, пятиугольник имеет пять диагоналей.

Шестиугольник:

Шестиугольник имеет шесть вершин. Диагонали шестиугольника соединяют несоседние вершины и образуют девять треугольников внутри шестиугольника. Таким образом, шестиугольник имеет девять диагоналей.

Также стоит отметить, что чем больше количество вершин у многоугольника, тем больше количество диагоналей в нем.

Пример диагоналей в треугольнике

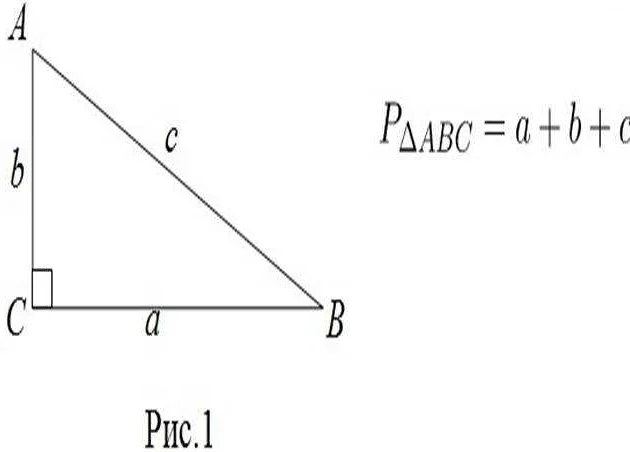
Рассмотрим треугольник ABC:

В треугольнике ABC можно выделить две диагонали:

Диагональ AC – отрезок, соединяющий вершины A и C, которые не являются соседними.

Диагональ AB – отрезок, соединяющий вершины A и B, которые не являются соседними.

Диагонали в треугольнике применяются, например, для нахождения центра окружности, вписанной в треугольник, а также для нахождения длин сторон треугольника по длинам его диагоналей.

Пример диагоналей в четырехугольнике

Примерами диагоналей в четырехугольнике могут быть следующие отрезки:

Пример 1: Рассмотрим четырехугольник ABCD. Диагональ AC соединяет вершины A и C, не являясь одной из его сторон.

Пример 2: Также в четырехугольнике ABCD можно найти диагональ BD, соединяющую вершины B и D, не являющуюся его стороной.

Эти диагонали разделяют многоугольник на три части: два треугольника и четырехугольник, образованный внутри четырехугольника.

Знание о диагоналях помогает в изучении свойств и характеристик четырехугольников, а также позволяет решать различные задачи с их участием.

Помните, что в четырехугольнике может быть несколько диагоналей, и приведенные примеры являются лишь наглядным их представлением.

Пример диагоналей в пятиугольнике

1. Диагональ, соединяющая первую вершину с третьей. Она пересекает две стороны пятиугольника, их можно обозначить как AB и CD. Такая диагональ образует угол, который может быть разным в каждом пятиугольнике.

2. Диагональ, соединяющая вторую вершину с четвертой. Она также пересекает две стороны пятиугольника, их можно обозначить как BC и DE. Угол, образованный этой диагональю, может быть разным в каждом пятиугольнике.

3. Диагональ, соединяющая первую вершину с пятой. Она также пересекает две стороны пятиугольника, их можно обозначить как AE и BD. Угол, образованный этой диагональю, может быть разным в каждом пятиугольнике.

Таким образом, в пятиугольнике имеется три диагонали, которые образуют различные углы и пересекают разные стороны. Изучение диагоналей в пятиугольнике помогает детям лучше понять геометрические свойства фигур и развивает их математическое мышление.

Пример диагоналей в шестиугольнике

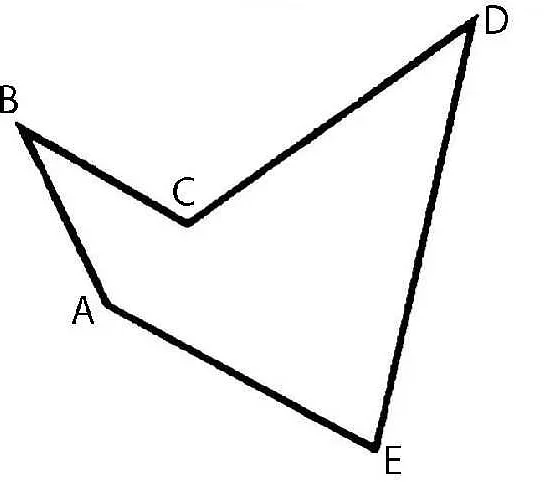
Рассмотрим пример шестиугольника и его диагоналей:

1. В шестиугольнике ABCDEF проведем диагональ AD — отрезок, соединяющий вершины A и D.
2. Также проведем диагональ BE — отрезок, соединяющий вершины B и E.
3. И проведем диагональ CF — отрезок, соединяющий вершины C и F.

Таким образом, в данном примере в шестиугольнике ABCDEF есть три диагонали — AD, BE и CF.

Диагонали в шестиугольнике могут иметь разные длины и углы между собой. Они могут быть пересекающимися или не пересекающимися.

Изучение диагоналей в шестиугольниках помогает учащимся лучше понять структуру и свойства многоугольников, а также развивает их пространственное мышление и логическое мышление.

Пример диагоналей в семиугольнике

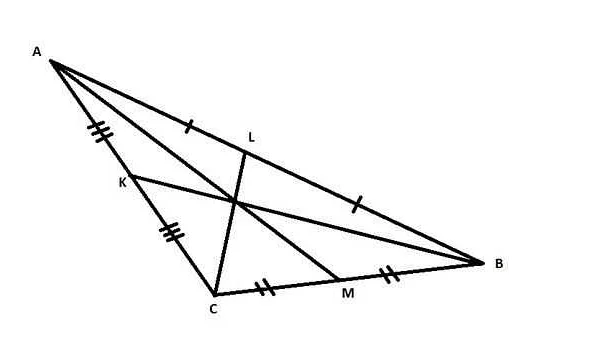
В семиугольнике есть четыре диагонали:

Номер диагоналиСоединяемые вершины

1	Вершина 1 и вершина 3
2	Вершина 2 и вершина 4
3	Вершина 3 и вершина 5
4	Вершина 4 и вершина 6

Диагонали в семиугольнике могут быть разной длины. Например, диагонали 1 и 3 могут быть короче диагоналей 2 и 4. Это зависит от размеров и формы семиугольника.

Пример диагоналей в восьмиугольнике

Рассмотрим восьмиугольник ABCDEFGH. В нем есть следующие диагонали:

ДиагональВершины

AC	A и C
AD	A и D
AE	A и E
AF	A и F
AG	A и G
AH	A и H
BC	B и C
BE	B и E
BH	B и H
CD	C и D
CF	C и F
CH	C и H
DE	D и E
DG	D и G
EF	E и F
EG	E и G
FG	F и G
GH	G и H

Таким образом, в восьмиугольнике имеется 18 диагоналей.

Вопрос-ответ:

Что такое диагональ многоугольника?

Диагональ многоугольника – это отрезок, который соединяет две его вершины, не являющиеся соседними.

Сколько диагоналей может быть у многоугольника?

Количество диагоналей в многоугольнике можно найти по формуле: n(n — 3) / 2, где n — количество вершин многоугольника. Например, у треугольника (n=3) нет диагоналей, у четырехугольника (n=4) — 2 диагонали, у пятиугольника (n=5) — 5 диагоналей и т.д.

Как проверить, является ли отрезок диагональю многоугольника?

Чтобы убедиться, что отрезок является диагональю многоугольника, нужно проверить два условия: 1) отрезок должен соединять две вершины, не являющиеся соседними; 2) отрезок не должен пересекать другие стороны или диагонали многоугольника.

Можно ли провести диагональ в многоугольнике с 6 вершинами?

Для многоугольника с 6 вершинами можно провести 9 диагоналей. Чтобы это проверить, можно воспользоваться формулой: n(n — 3) / 2. В данном случае получим: 6(6 — 3) / 2 = 6 диагоналей.