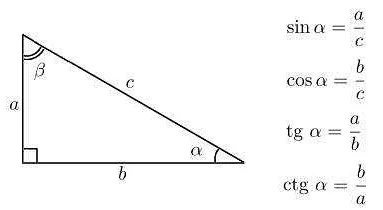
Что такое биссектриса математика

Биссектриса — это линия или отрезок, который делит угол на две равные части. В математике биссектриса играет важную роль при решении различных задач и нахождении неизвестных значений углов. Узнайте больше о понятии биссектрисы и ее применении в этой статье.

Биссектриса — одно из важных понятий в геометрии, которое играет значительную роль при решении различных задач. Биссектрисой называется прямая, которая делит угол пополам. Иными словами, биссектриса является линией, которая проходит через вершину угла и делит его на два равных угла.

Биссектриса может быть найдена для любого угла, независимо от его величины. Она всегда перпендикулярна стороне угла и делит ее на две отрезка, пропорциональных друг другу. Причем отношение этих отрезков равно отношению длин двух других сторон этого угла.

Важно отметить, что биссектриса имеет множество применений в геометрии. Она помогает решать задачи по нахождению неизвестных углов и длин сторон. Также биссектриса используется при построении и анализе треугольников, многоугольников и других геометрических фигур.

Биссектриса имеет важное значение не только в геометрии, но и в других областях математики. Она широко используется в теории вероятностей, а также в алгебре и анализе. Знание и понимание биссектрисы помогает студентам и ученым решать различные математические задачи и проблемы.

Что такое биссектриса?

Биссектриса может быть внутренней или внешней в зависимости от того, находится ли она внутри угла или за его пределами. Внутренняя биссектриса делит угол на два равных угла, а внешняя биссектриса делит внешнюю область угла на две равные части.

Биссектриса может быть построена с помощью компаса и линейки. Для построения внутренней биссектрисы нужно провести две дуги равного радиуса с центром в вершине угла. Затем проводится линия, проходящая через вершину угла и точку пересечения дуг.

Биссектриса имеет ряд важных свойств и применений. Например, она может быть использована для нахождения центра окружности, вписанной в треугольник. Также в геометрии биссектриса является одной из базовых линий, которые используются для доказательства различных теорем и свойств углов.

Важно отметить, что биссектриса не является единственной линией, которая делит угол пополам. Также существуют медиана и высота угла, но их определения и свойства отличаются от биссектрисы.

Определение

Биссектриса может быть проведена внутри или снаружи угла. Если биссектриса проведена внутри угла, то она пересекает его стороны. Если биссектриса проведена снаружи угла, то она продолжает одну из его сторон.

Биссектриса играет важную роль в геометрии, так как она используется для решения различных задач. Например, с помощью биссектрисы можно найти серединный перпендикуляр к отрезку, найти центр описанной окружности треугольника и многое другое.

Знание свойств и применения биссектрисы позволяет решать разнообразные геометрические задачи и углубляться в изучение геометрии.

Биссектриса в треугольнике

Биссектриса в треугольнике имеет несколько важных свойств и применений:

СвойствоПрименение

Биссектриса делит противоположную сторону в отношении, равном отношению соответствующих боковых сторон треугольника.	Позволяет находить отношения длин сторон треугольника и решать задачи, связанные с пропорциональностью.
Биссектрисы трех углов треугольника пересекаются в одной точке, называемой центром вписанной окружности.	С помощью центра вписанной окружности можно решать задачи о построении треугольника или нахождении его свойств.
Биссектрисы трех углов треугольника образуют окружность, называемую окружностью Эйлера.	Окружность Эйлера имеет много важных свойств и применений в геометрии и математике.

Таким образом, биссектриса в треугольнике играет важную роль в решении геометрических задач и нахождении свойств треугольника.

Биссектриса в угле

Когда мы говорим о биссектрисе в угле, мы имеем в виду линию, которая проходит через вершину угла и делит его на два равных участка. Биссектриса угла является перпендикулярной к стороне угла и проходит через его вершину.

Биссектриса угла имеет несколько важных свойств и применений. Одно из них – это нахождение точки пересечения биссектрисы с противоположной стороной угла. Эта точка называется точкой биссектрисы и является центром вписанной окружности в данный угол.

Биссектриса также используется для нахождения угла между двумя прямыми линиями, когда известна их наклонная. В этом случае биссектриса является осью симметрии между этими линиями.

Знание и понимание свойств биссектрисы в угле позволяет решать различные геометрические задачи и использовать их в практических ситуациях. Биссектриса является одним из базовых понятий геометрии, которое широко применяется в различных областях знания.

Свойства биссектрисы

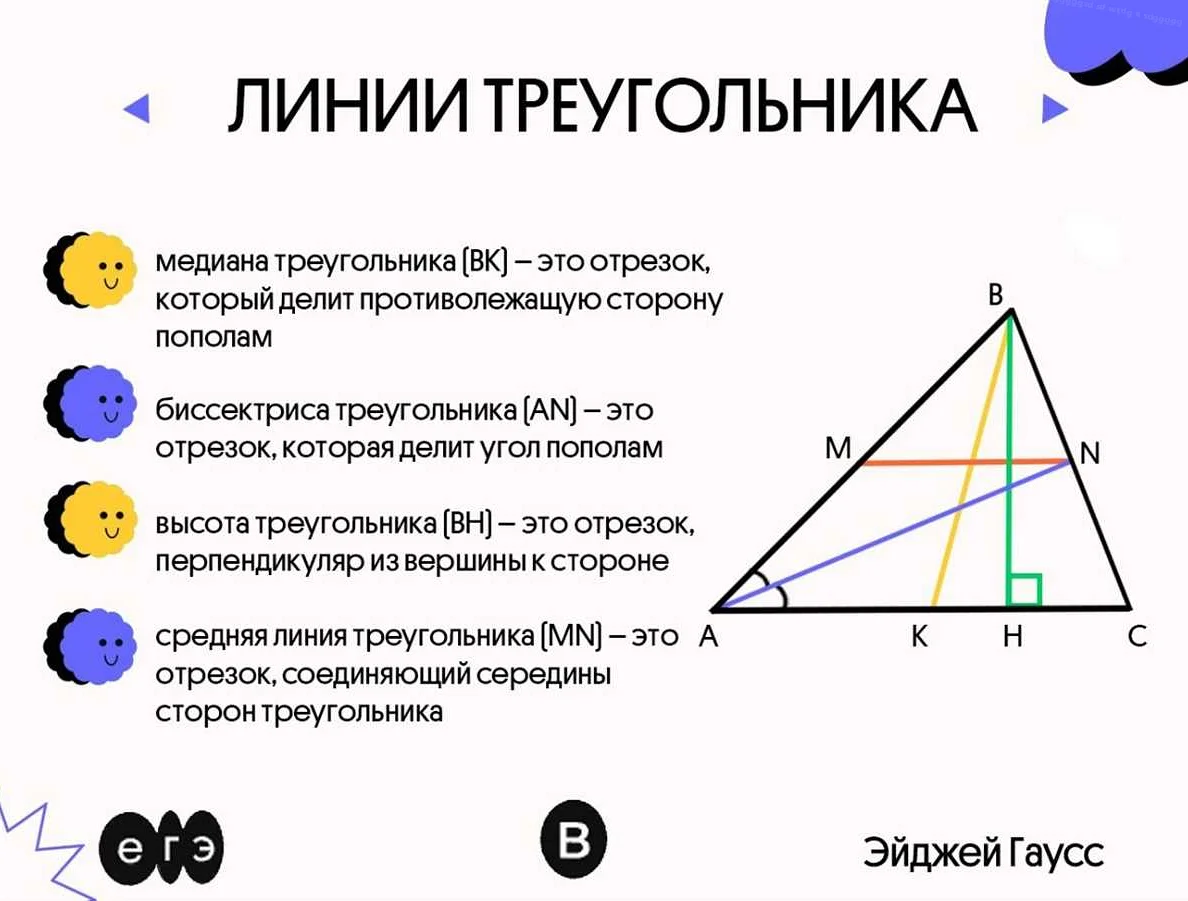
1. Биссектриса угла является отрезком, который соединяет вершину угла с серединой противоположной стороны.
2. Биссектриса угла делит противоположную сторону на две отрезка, которые имеют одинаковую длину.
3. Точка пересечения биссектрисы угла с противоположной стороной является точкой биссектрисы.
4. Если из вершины угла провести биссектрису, то угол, образованный этой биссектрисой и одной из сторон угла, будет равным половине исходного угла.
5. Биссектриса угла является осью симметрии для угла, она делит его на две равные части.

Свойства биссектрисы являются важными в математике и имеют широкое применение в геометрии, в частности при решении задач на построение и вычисление углов.

Свойство равенства углов

Это свойство может быть использовано для решения различных задач, связанных с углами. Например, если известно, что два угла равны, то можно использовать свойство равенства углов, чтобы найти длину и положение их биссектрисы.

Свойство перпендикулярности

Пусть AB – сторона треугольника, а BD – биссектриса угла A. Тогда верно следующее утверждение: BD перпендикулярна к AB.

Это свойство легко доказать. Рассмотрим треугольник ABD. Так как BD – биссектриса угла A, то угол ABD равен углу ADB. В свою очередь, угол ABD является внутренним углом треугольника ABD. Но внутренние углы треугольника в сумме равны 180°. Значит, углы ABD и ADB в сумме дают 180°. Так как они равны, то каждый из них равен 90°. Другими словами, угол ABD прямой. А значит, BD перпендикулярна к AB.

Из этого свойства следует, что биссектрисы двух углов, заключающихся на одной и той же стороне треугольника, перпендикулярны друг другу. То есть, если BD1 и BD2 – биссектрисы углов A и C соответственно, то BD1 перпендикулярна к BC, а BD2 перпендикулярна к AB. Кроме того, угол BDC2 также является прямым.

Применение

Биссектриса играет важную роль в различных областях математики и геометрии. Вот некоторые из её применений:

1. Геометрия треугольника: Биссектриса используется для нахождения центра вписанной окружности треугольника. Она также помогает определить длины отрезков, на которые биссектриса делит стороны треугольника.

2. Углы: Биссектриса используется для нахождения половины угла. Она делит угол на два равных угла.

3. Геометрия окружности: Биссектриса используется для нахождения радиуса окружности, проведенной касательно к окружности в данной точке.

4. Построение: Биссектриса может быть использована для построения равных углов и отрезков.

5. Геометрические задачи: Биссектриса помогает решить различные геометрические задачи, включая поиск углов, длин отрезков и нахождение центров окружностей.

6. Статистика: Биссектриса может быть использована для разделения данных на две равные группы.

Как видно, биссектриса имеет много применений и играет важную роль в геометрии и других областях математики.

Использование биссектрисы при нахождении площади треугольника

Для нахождения площади треугольника по биссектрисе, можно воспользоваться следующей формулой:

1. Найдите длины всех сторон треугольника.
2. Найдите полупериметр треугольника, который равен сумме длин всех сторон, деленной на 2.
3. Используя полупериметр и длины сторон, найдите радиус вписанной окружности треугольника по формуле: r = √((p-a)(p-b)(p-c))/p, где p — полупериметр, а a, b, c — длины сторон.
4. Вычислите площадь треугольника по формуле: S = r * p, где r — радиус вписанной окружности, а p — полупериметр.

Таким образом, используя биссектрису и формулу для нахождения площади треугольника, можно достаточно точно вычислить его площадь без необходимости знания высоты или других параметров треугольника.

Вопрос-ответ:

Что такое биссектриса?

Биссектриса — это линия или отрезок, который делит угол на две равные части. Она проходит через вершину угла и перпендикулярна его сторонам.

Как определить биссектрису угла?

Чтобы найти биссектрису угла, нужно провести две линии или отрезка, выходящих из вершины угла и пересекающих его стороны. Затем нужно провести прямую, которая делит угол на две равные части. Эта прямая и будет биссектрисой угла.

Какие свойства имеет биссектриса?

Биссектриса угла делит его на две равные части, поэтому любая точка на биссектрисе равноудалена от сторон угла. Также, если в треугольнике проведены биссектрисы трех углов, они пересекаются в одной точке, называемой центром вписанной окружности.

Где можно применить знание о биссектрисе?

Знание о биссектрисе угла может быть полезным при решении геометрических задач, например, при нахождении поперечника окружности, вписанной в треугольник. Также биссектрисы углов играют важную роль при измерении углов и проведении параллельных линий.

Использование биссектрисы при нахождении длины стороны треугольника

Для нахождения длины стороны треугольника с помощью биссектрисы можно воспользоваться теоремой биссектрисы. Согласно этой теореме, биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные другим двум сторонам треугольника.

Используя данную теорему, можно найти длину стороны треугольника. Для этого необходимо известными величинами являются длины двух сторон треугольника и длина биссектрисы, проведенной из вершины угла, находящегося против третьей стороны.

Процесс нахождения длины стороны треугольника с использованием биссектрисы может быть описан следующими шагами:

1. Найдите длины двух известных сторон треугольника и длину биссектрисы.
2. Примените теорему биссектрисы, чтобы найти отрезок, на который биссектриса делит противоположную сторону треугольника.
3. Используйте найденное отношение, чтобы выразить длину неизвестной стороны треугольника через длины сторон, известные величины и длину биссектрисы.
4. Решите полученное уравнение, чтобы найти длину неизвестной стороны треугольника.

Использование биссектрисы при нахождении длины стороны треугольника является одним из примеров практического применения данного математического инструмента. Биссектриса также может быть использована для нахождения других параметров треугольника, таких как площадь или высоты.

Видео по теме: