Что такое прямые в математике

Прямые в математике — это линии, которые не имеют выпуклости или изгибов. Они представляют собой самые простые геометрические объекты и определяются двумя точками или уравнением. Прямые широко используются в различных областях математики и физики, и представляют собой важный инструмент для изучения отношений между точками и линиями.

В математике прямая является одной из основных геометрических фигур, которая обладает рядом особых свойств и играет важную роль в различных областях науки. Прямая — это бесконечно тонкая и бесконечно протяженная линия, которая не имеет ни начала, ни конца.

Прямая характеризуется несколькими основными свойствами. Во-первых, любые две точки на прямой можно соединить отрезком, который будет лежать полностью на этой прямой. Кроме того, прямая делит плоскость на две полуплоскости. В каждой полуплоскости все точки расположены с одной стороны от прямой.

Прямые могут быть вертикальными, горизонтальными или наклонными. Вертикальная прямая проходит перпендикулярно горизонтальной плоскости и имеет угол наклона 90 градусов. Горизонтальная прямая, наоборот, лежит в горизонтальной плоскости и имеет угол наклона 0 градусов. Наклонная прямая имеет угол наклона, отличный от 0 и 90 градусов.

Примерами прямых могут служить отрезок между двумя точками, луч, биссектриса угла и множество других геометрических фигур. Прямые играют важную роль в алгебре, геометрии, физике и других областях науки. Они используются для решения различных задач, моделирования реальных объектов и разработки алгоритмов.

Определение прямой в математике

Главное свойство прямой — это то, что любые две ее точки можно соединить отрезком, который полностью лежит на самой прямой. Также прямая не имеет начала или конца, она простирается в бесконечность в обоих направлениях.

Прямая может быть задана различными способами. Например, она может быть задана уравнением вида y = mx + b, где m — угловой коэффициент, а b — свободный член. Также прямая может быть определена двумя точками, через которые она проходит. В математике прямая обозначается символом «l» или «AB», где A и B — две точки, через которые она проходит.

Прямая является основой для многих других геометрических фигур, таких как отрезки, полупрямые и углы. Она также играет важную роль в решении различных математических задач и построении графиков функций.

Видео по теме:

Свойства прямой

• Прямая имеет все точки, лежащие на ней, и не имеет точек, которые не лежат на ней.
• Любые две точки на прямой определяют ее полностью.
• Прямая не имеет ширины и толщины, она является одномерным объектом.
• Прямая имеет бесконечное количество точек, которые расположены вдоль нее.
• Прямая можно продлить бесконечно в обе стороны.

Эти свойства помогают нам лучше понять и работать с прямыми и использовать их в решении математических задач.

Уравнение прямой

y = mx + b

где y — координата по оси OY, x — координата по оси OX, m — наклон (угловой коэффициент) прямой, и b — свободный член.

Наклон прямой, задаваемой уравнением, определяется коэффициентом m. Если m положительное число, то прямая наклонена вверх (отлежит от оси OX в положительном направлении), если отрицательное — то прямая наклонена вниз (отлежит от оси OX в отрицательном направлении). Если m равно нулю, то прямая параллельна оси OX.

Свободный член b — это точка пересечения прямой с осью OY. Если b равен нулю, то прямая проходит через начало координат.

Таким образом, уравнение прямой позволяет нам однозначно определить каждую точку на прямой и описать ее геометрические свойства.

Геометрическое представление прямой

Прямая может быть представлена в виде графика на координатной плоскости. Для этого необходимо задать две точки, через которые проходит прямая. Затем, используя эти точки, можно построить график, который представляет собой линию, проходящую через эти точки.

Если прямая проходит через точку (0,0) и имеет угловой коэффициент k, то уравнение прямой может быть записано в виде y = kx. Примером такой прямой может служить линия, проходящая через точки (0,0) и (1,2). В этом случае угловой коэффициент равен 2, и уравнение прямой будет иметь вид y = 2x.

Геометрическое представление прямой позволяет анализировать ее свойства, такие как наклон, длина, углы и точки пересечения с другими прямыми или фигурами. Кроме того, оно помогает решать задачи, связанные с поиском расстояния между точками на прямой и нахождением точек пересечения с другими линиями.

СвойствоОписание

Наклон	Угловой коэффициент определяет наклон прямой относительно оси x.
Длина	Прямая может иметь ограниченную или бесконечную длину.
Углы	Прямые могут образовывать углы друг с другом.
Точки пересечения	Прямые могут пересекаться или не пересекаться с другими прямыми или фигурами.

Примеры прямых в математике

Вот некоторые примеры прямых в математике:

1. Вертикальная прямая: это прямая, которая идет вверх или вниз и параллельна оси y. Она имеет уравнение вида x = c, где c — константа. Например, прямая x = 2 будет вертикальной прямой, которая проходит через все точки с x-координатой 2.

2. Горизонтальная прямая: это прямая, которая идет влево или вправо и параллельна оси x. Она имеет уравнение вида y = c, где c — константа. Например, прямая y = -3 будет горизонтальной прямой, которая проходит через все точки с y-координатой -3.

3. Наклонная прямая: это прямая, которая идет вверх или вниз и не является ни вертикальной, ни горизонтальной. Она имеет уравнение вида y = mx + b, где m — наклон прямой, а b — точка пересечения с осью y (y-перехват). Например, прямая y = 2x + 1 будет наклонной прямой, которая идет вверх с наклоном 2 и пересекает ось y в точке (0, 1).

Это лишь несколько примеров прямых в математике. Прямые используются для моделирования и анализа различных явлений, от геометрических конструкций до физических законов. Изучение свойств и применений прямых является важной частью математического образования и науки в целом.

Прямая как наиболее короткий путь между двумя точками

Свойство прямой как наиболее короткого пути можно объяснить с помощью принципа наименьшего действия. Если мы хотим добраться из точки A в точку B, то идти по прямой будет наиболее быстро и экономично, поскольку это позволяет нам пройти самое короткое расстояние. В противном случае, если мы выберем не прямой путь, нам придется пройти больше расстояния, что займет больше времени и энергии.

Прямые имеют несколько важных свойств:

1.	Прямая не имеет начала и конца.
2.	Прямая имеет бесконечное количество точек.
3.	Прямая может быть ограничена другими линиями или поверхностями.

Примером прямой может служить отрезок между двумя точками на плоскости или прямая, заданная уравнением вида y = kx + b, где k и b — коэффициенты.

Прямые имеют важное значение в геометрии и математическом анализе, так как они позволяют решать множество задач, связанных с изучением пространства и движения объектов.

Прямая как граница между двумя полуплоскостями

Прямая может служить границей между двумя полуплоскостями в различных геометрических задачах. Например, в геометрии треугольников прямая может быть использована для построения медианы, биссектрисы или высоты, которые делят треугольник на две равные полуплоскости.

Также, прямая может быть использована для разделения плоскости на две части в задачах графики. Например, при построении графика функции, прямая может быть использована для разделения области, где функция положительна, и области, где функция отрицательна.

Прямая как граница между двумя полуплоскостями играет важную роль в различных математических и геометрических задачах, позволяя разделять пространство на две части и рассматривать их отдельно для более удобного анализа и решения задач.

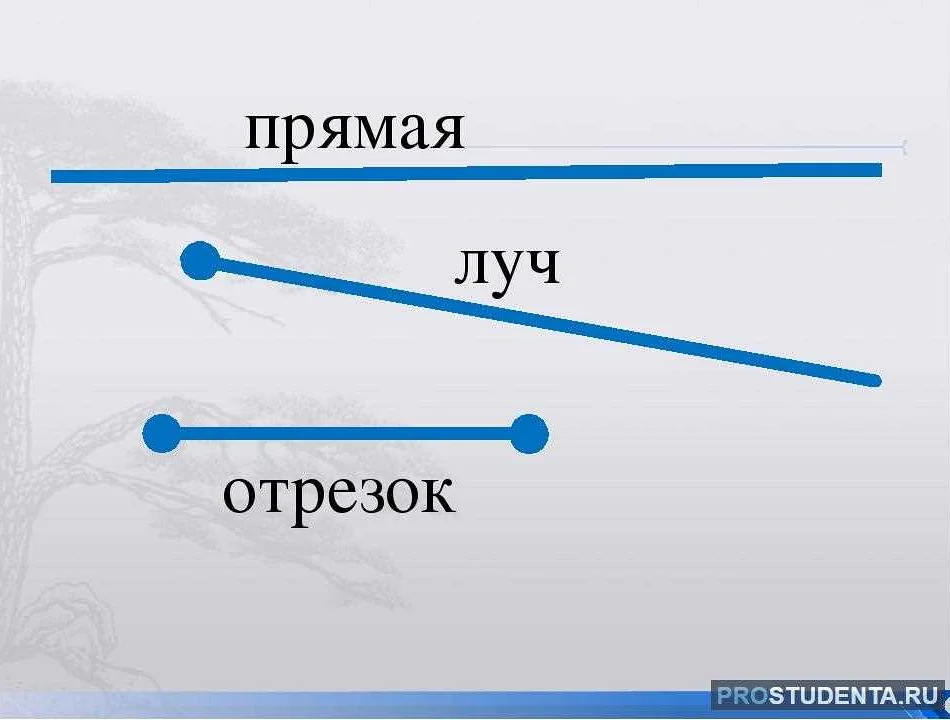
Прямая как наклонная линия на графике

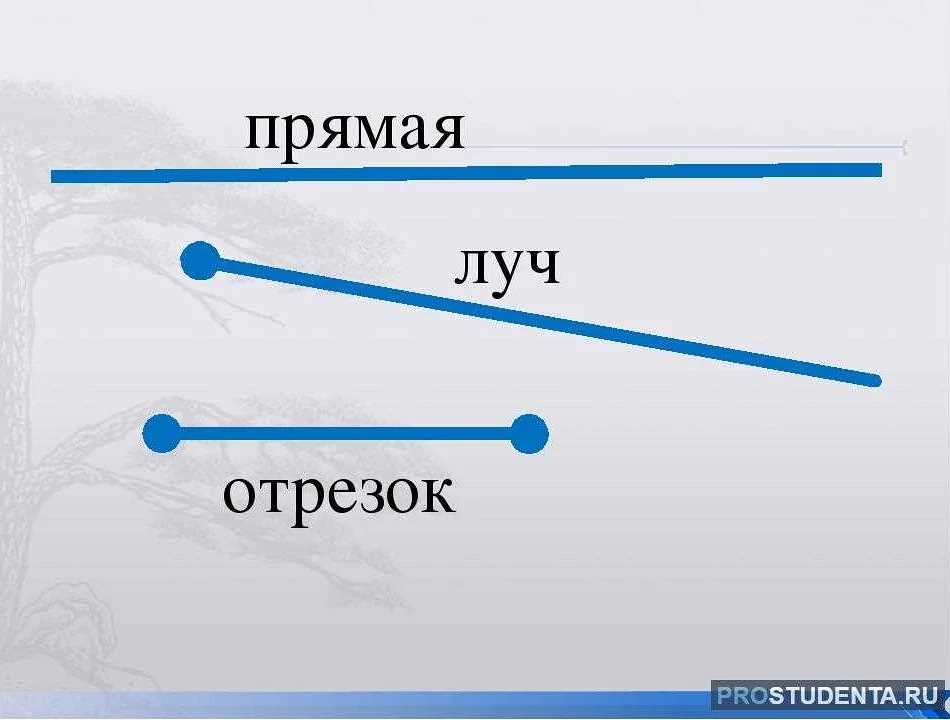
Наклонная линия – это прямая, которая имеет определенный угол наклона и проходит через две точки на плоскости. При построении графика функции, наклонная линия показывает зависимость между двумя переменными. Угол наклона определяет, насколько быстро меняется одна переменная по отношению к другой.

Для построения наклонной линии на графике необходимо знать координаты двух точек, через которые она проходит. Зная эти координаты, можно определить угол наклона и нарисовать линию, которая соединяет эти точки. Если угол наклона положителен, то прямая будет идти вверх, если отрицателен – вниз. Если угол наклона равен нулю, то прямая будет горизонтальной, а если бесконечно велик или отсутствует, то прямая будет вертикальной.

Примером наклонной линии на графике может служить график зависимости скорости автомобиля от времени. Пусть у нас есть данные о скорости автомобиля в разные моменты времени: 0 секунд – 0 км/ч, 1 секунда – 10 км/ч, 2 секунды – 20 км/ч и т.д. Построив график этих данных на плоскости, мы получим наклонную линию, которая будет идти вверх с положительным углом наклона, показывая, что скорость автомобиля увеличивается с течением времени.

Вопрос-ответ:

Что такое прямая в математике?

Прямая — это геометрическая фигура, состоящая из бесконечного числа точек, которые лежат на одной линии и не имеют никаких изгибов или углов.

Какие свойства имеют прямые в математике?

Прямые обладают несколькими важными свойствами. Они имеют бесконечную длину, то есть могут быть продолжены в обе стороны. Прямые также не имеют ширины и толщины. Каждая точка на прямой является ее частью, и любые две точки на прямой можно соединить отрезком.

Как можно задать прямую в математике?

Прямую можно задать с помощью уравнения. Например, y = mx + b, где m — угловой коэффициент, а b — свободный член. Угловой коэффициент определяет наклон прямой, а свободный член — точку, через которую проходит прямая.

Какие примеры прямых можно привести?

Примеры прямых в математике могут быть разнообразными. Например, вертикальная прямая, которая не имеет углового коэффициента и задается уравнением x = a, где a — это константа. Горизонтальная прямая задается уравнением y = b, где b — это константа. Еще один пример — наклонная прямая, заданная уравнением y = mx + b, где m — угловой коэффициент.

Как можно определить, параллельны ли две прямые?

Две прямые называются параллельными, если они никогда не пересекаются и имеют одинаковый угловой коэффициент. Если угловые коэффициенты двух прямых равны, то они параллельны.