Линия что это в математике

Линия в математике — это геометрическая фигура, состоящая из бесконечного числа точек, простирающаяся в обоих направлениях без конца. Линии широко используются в алгебре, геометрии и физике для описания и изучения пространства, форм и движения.

Линия – это геометрическая фигура, которая представляет собой множество бесконечных точек, расположенных на одной прямой. Линии играют важную роль в математике, так как они служат основой для изучения многих других понятий и конструкций. Они используются для решения различных задач и моделирования реальных объектов и явлений.

В математике выделяют несколько видов линий. Прямая линия – это наиболее простая форма линии, которая не имеет изгибов и кривизны. Прямая может быть бесконечной в обоих направлениях или иметь конечную длину. Кривая линия – это линия, которая может иметь изгибы и кривизну. Кривые могут быть замкнутыми или разомкнутыми. Также существуют различные типы кривых, такие как парабола, эллипс, гипербола и др.

Линии используются во многих областях математики и науки. Например, в геометрии линии используются для построения и изучения геометрических фигур. В физике линии используются для описания траекторий движения объектов. В экономике линии используются для построения графиков и анализа экономических данных. В компьютерной графике линии используются для создания изображений и анимации. В общем, линии – это неотъемлемая часть математики и широко применяются в различных сферах науки и техники.

Линия в математике: основное понятие и его значение

Значение линии в математике заключается в ее способности представлять различные объекты и явления. Линии могут быть использованы для представления пространственных отношений, изображения графиков функций, построения геометрических моделей и многое другое.

В математике существуют различные виды линий, каждая из которых имеет свои особенности и применение. Некоторые из наиболее распространенных видов линий включают:

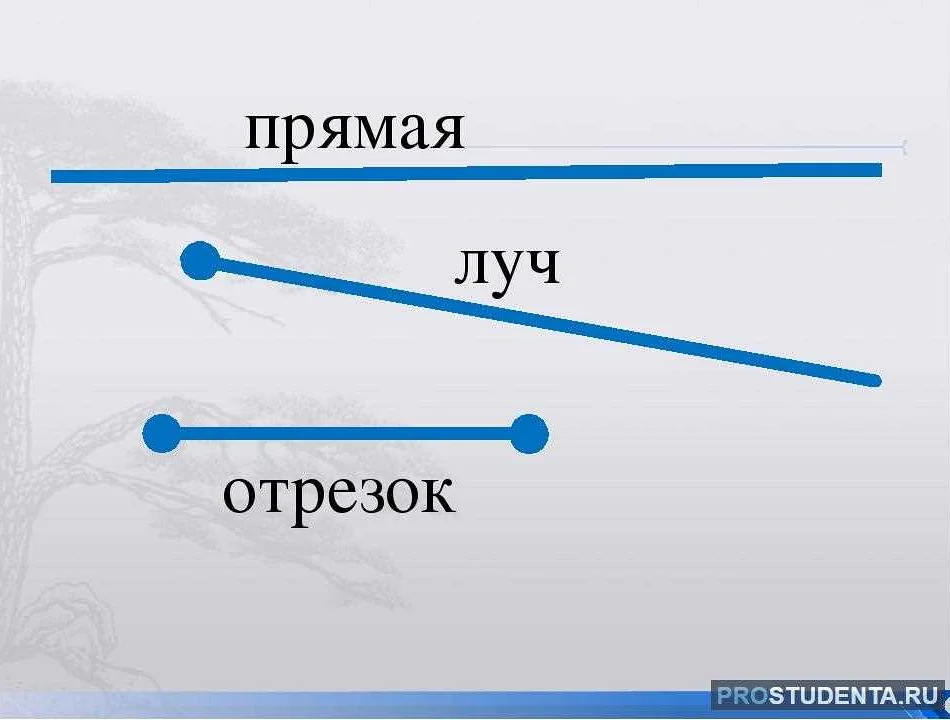
• Прямую линию — это линия, которая не имеет изгибов или пересечений. Она состоит из всех точек, которые лежат на одной прямой.
• Отрезок — это фрагмент прямой линии, который ограничен двумя конечными точками.
• Ломаную линию — это линия, состоящая из отрезков, соединенных конечными точками.
• Кривую линию — это линия, которая имеет изгибы и может быть описана уравнением.
• Окружность — это линия, состоящая из всех точек, которые находятся на одинаковом расстоянии от центра.

Каждый из этих видов линий имеет свои свойства и применение в различных областях математики. Изучение линий позволяет анализировать и представлять различные математические и физические явления, а также строить сложные математические модели.

История возникновения и развития понятия «линия»

Первые представления о линии появились в Древней Греции. Великий математик Евклид определил линию как непрерывное множество точек, которое не имеет ни длины, ни ширины. Евклид различал несколько видов линий: прямую, кривую и ломаную.

В средние века и Ренессансе понятие «линия» развивалось дальше. Великие ученые и математики, такие как Николай Коперник, Леонардо да Винчи и Галилео Галилей, продолжали исследования в области геометрии и вносили свои открытия и предложения.

В XIX веке математика и геометрия стали более строго оформленными научными дисциплинами. В этот период были разработаны аксиоматические системы, которые позволяли строго определить понятие «линия». Одним из важных результатов была классификация линий на пространственные и плоские.

В XX веке с развитием компьютерных технологий и появлением новых математических методов, понятие «линия» получило еще большее развитие. Сейчас линии широко применяются в различных областях, таких как инженерия, архитектура, компьютерная графика и дизайн.

ПериодОсновные открытия и исследования

Древняя Греция	Евклид определяет понятие «линия»
Средние века и Ренессанс	Исследования Николая Коперника, Леонардо да Винчи, Галилео Галилея
XIX век	Разработка аксиоматических систем и классификация линий
XX век	Развитие компьютерных технологий и новых математических методов

История возникновения и развития понятия «линия» является важной частью истории математики и геометрии. Знание этой истории позволяет лучше понять и оценить значимость этого понятия в современном мире.

Виды линий в математике: прямая, кривая, сегмент, отрезок

В математике существуют различные виды линий, которые могут быть классифицированы по своим характеристикам и свойствам.

Прямая – это линия, которая не имеет ни начала, ни конца. Она простирается бесконечно в обе стороны и не имеет никаких изгибов или кривых.

Кривая – это линия, которая имеет изгибы и может быть изогнута в различных направлениях. Кривая может быть замкнутой или незамкнутой, гладкой или разрывной.

Сегмент – это часть линии, ограниченная двумя точками. В отличие от прямой или кривой, сегмент имеет конечную длину и может быть прямолинейным или изогнутым.

Отрезок – это сегмент, который соединяет две точки. Отрезок является прямолинейным и имеет конечную длину, которая определяется расстоянием между двумя точками.

Все эти виды линий имеют свои особенности и применяются в различных областях математики и физики для изучения геометрических отношений и решения различных задач.

Вид линииОписание

Прямая	Линия без начала и конца
Кривая	Линия с изгибами и изогнутостями
Сегмент	Часть линии, ограниченная двумя точками
Отрезок	Сегмент, соединяющий две точки

Геометрические свойства линий: параллельность, пересечение, смежность

Линии в геометрии могут обладать различными свойствами, которые определяют их взаимное расположение и взаимодействие. Рассмотрим основные геометрические свойства линий: параллельность, пересечение и смежность.

Параллельность — это свойство двух или более линий, которые находятся на одной плоскости и никогда не пересекаются. Параллельные линии обозначаются двумя параллельными знаками (||). Например, две прямые AB и CD, если они находятся на одной плоскости и не пересекаются, считаются параллельными: AB || CD.

Пересечение — это свойство двух или более линий, которые имеют общую точку. Точка пересечения линий обозначается символом «∩». Например, две пересекающиеся прямые AB и CD имеют общую точку O: AB ∩ CD = O.

Смежность — это свойство двух или более линий, которые имеют общий конечный или начальный пункт. Смежные линии могут быть как параллельными, так и пересекающимися. Например, линии AB и BC являются смежными, так как они имеют общую точку B.

Знание геометрических свойств линий позволяет анализировать и решать различные задачи в геометрии и других областях математики. Они играют важную роль в построении и изучении геометрических фигур, а также в применении геометрии в реальных ситуациях.

Арифметические операции с линиями: сложение, вычитание, умножение

Сложение линий:

Сложение линий представляет собой процесс объединения двух или более линий в одну. Для выполнения сложения линий необходимо найти точки пересечения каждой пары линий и соединить их, образуя новую линию.

Если линии имеют одинаковый наклон, то новая линия будет иметь такой же наклон, а ее смещение будет равно сумме смещений исходных линий.

Если линии имеют разный наклон, то новая линия будет иметь средний наклон между наклонами исходных линий, а ее смещение будет определяться соответствующим образом.

Вычитание линий:

Вычитание линий представляет собой процесс удаления одной линии из другой. Для выполнения вычитания линий необходимо найти точки пересечения между линиями и удалить соответствующую часть из исходной линии.

Если линии имеют одинаковый наклон, то вычитание линий сводится к удалению смещения одной линии из смещения другой линии.

Если линии имеют разный наклон, то вычитание линий может быть более сложным и требовать использования дополнительных математических методов.

Умножение линий:

Умножение линий представляет собой процесс масштабирования линии по горизонтали и вертикали. Для выполнения умножения линии необходимо умножить ее координаты на определенный множитель.

Умножение линии на положительное число приведет к увеличению ее размера, а умножение на отрицательное число — к перевороту и отражению линии.

Умножение линий может применяться для создания различных эффектов и трансформаций в графическом дизайне и компьютерной графике.

Линия как элемент графических представлений: графики функций и диаграммы

Для построения графика функции необходимо задать набор точек, каждая из которых состоит из значений аргумента и функции. Затем эти точки соединяются линией, что позволяет визуально представить форму графика. График функции может быть положительным или отрицательным, возрастающим или убывающим, иметь различные перегибы и точки экстремума.

Диаграмма является еще одним способом визуального представления данных. Она используется для сравнительного анализа или отображения различных категорий и их соотношений. Диаграммы могут быть гистограммами, круговыми диаграммами, линейными диаграммами и т.д. Во всех этих типах диаграмм линия является ключевым элементом, который отображает соотношения или изменение данных.

Тип диаграммыОписание

Гистограмма	Показывает количество или частоту появления значений в определенном интервале.
Круговая диаграмма	Показывает соотношение долей различных категорий по отношению к целому.
Линейная диаграмма	Показывает изменение данных во времени или по другой шкале.

Все эти типы диаграмм используют линию для визуального представления данных и их соотношений. Линия является главным элементом, который позволяет анализировать данные и делать выводы о соотношениях между различными значениями.

Применение линий в пространстве: построение и измерение

Применение линий в пространстве имеет свои особенности. Построение линий в трехмерном пространстве требует использования дополнительных инструментов и методов. Вместо простого определения двух точек, линия в пространстве определяется тремя точками или векторами. Также можно использовать параметрическое представление линии с помощью уравнений, которые описывают ее положение в пространстве.

Измерение линий в пространстве также имеет свои особенности. Вместо простого измерения длины, линия в трехмерном пространстве может иметь дополнительные характеристики, такие как направление, угол наклона или кривизна. Для измерения линий в пространстве используются специальные инструменты, такие как трехмерные координатные системы или лазерные уровни.

Применение линий в пространстве находит свое применение в различных областях. Например, в архитектуре линии используются для построения планов зданий, проектирования фасадов и создания интерьеров. В инженерии линии применяются для построения трехмерных моделей, проектирования механизмов и определения точных координат объектов. В физике линии используются для описания траекторий движения тел и электромагнитных полей.

Таким образом, применение линий в пространстве играет важную роль в различных областях науки и техники. Построение и измерение линий в трехмерном пространстве требует специальных инструментов и методов. Понимание особенностей применения линий в пространстве позволяет успешно решать задачи, связанные с анализом и моделированием трехмерных объектов.

Видео по теме:

Вопрос-ответ:

Что такое линия в математике?

Линия в математике — это геометрическая фигура, представляющая собой набор бесконечно маленьких точек, расположенных на одной прямой.

Какие виды линий бывают в математике?

В математике существуют различные виды линий, включая прямую линию, кривую линию, замкнутую линию и отрезок. Каждый вид линии имеет свои уникальные свойства и характеристики.

Каким образом линии применяются в математике?

Линии в математике играют важную роль в геометрии и анализе. Они используются для изучения форм, расстояний и углов. Они также являются основой для создания графиков и диаграмм, которые помогают визуализировать и анализировать данные.

Как определить, что две линии параллельны?

Две линии считаются параллельными, если они никогда не пересекаются и всегда остаются на одинаковом расстоянии друг от друга. Это можно проверить, используя геометрические методы, такие как измерение углов, использование особенностей фигур и конструкцию параллельных линий.

Какие свойства имеет прямая линия?

Прямая линия имеет несколько свойств. Она является самым коротким расстоянием между двумя точками и не имеет ни начала, ни конца. Прямая также продолжается в бесконечность в обе стороны и делит плоскость на две части.

Что такое линия в математике?

Линия в математике — это понятие, обозначающее бесконечно тонкое и прямое образование, состоящее из бесконечно маленьких точек. Она не имеет толщины и длины, но имеет направление и протяженность.

Линии в технических и инженерных расчетах: применение в строительстве и архитектуре

Линии играют важную роль в технических и инженерных расчетах, особенно в строительстве и архитектуре. Они используются для создания планов, чертежей, схем и других технических документов.

Одним из основных видов линий, применяемых в строительстве и архитектуре, является линия контура. Она используется для обозначения формы и размеров зданий, сооружений и других объектов. Линия контура помогает определить границы объекта и его основные характеристики.

Еще одним важным видом линии является линия разреза. Она используется для показа внутренней структуры объекта, например, стен, перекрытий, фундамента и других элементов конструкции. Линия разреза помогает инженерам и архитекторам понять, как устроены объекты изнутри и как они взаимодействуют между собой.

Еще одним важным видом линии является линия проекции. Она используется для показа объектов и их частей во взаимосвязи с плоскостью проекции. Линия проекции помогает инженерам и архитекторам представить объекты в трехмерном пространстве на плоскости чертежа или схемы.

Кроме того, в строительстве и архитектуре часто используются различные виды линий для обозначения осей, размеров, уровней и других характеристик объектов. Например, линия оси используется для обозначения центральной оси объекта, линия уровня помогает обозначить горизонтальное положение объекта на местности, а линия размера используется для указания размеров объектов и их частей.

В заключение, линии являются неотъемлемой частью технических и инженерных расчетов в строительстве и архитектуре. Они позволяют визуально представить объекты, определить их форму, размеры и взаимное расположение. Без использования линий было бы трудно создавать точные и понятные технические документы, необходимые для успешного выполнения проектов в строительстве и архитектуре.

Линии в компьютерной графике: создание и анимация

Создание линий в компьютерной графике осуществляется с помощью алгоритмов, которые определяют координаты и цвет каждого пикселя на экране, через которые должна проходить линия. Существуют различные алгоритмы построения линий, такие как алгоритм Брезенхема и алгоритм Дэвиса-Стейнберга.

Анимация линий в компьютерной графике позволяет создавать движущиеся объекты и эффекты. Для анимации линий используются различные методы, такие как изменение их координат или цвета с течением времени. Анимированные линии могут быть использованы для создания плавных переходов, эффектов движения или изменения формы объектов.

Виды линийОписание

Прямая линия	Линия, которая соединяет две точки без промежуточных изгибов или углов.
Кривая линия	Линия, которая имеет изгибы и может быть задана с помощью математических уравнений или сплайнов.
Сегментированная линия	Линия, состоящая из нескольких отрезков, которые могут иметь различные углы и длины.
Контурная линия	Линия, которая образует контур объекта и определяет его форму.

Линии в компьютерной графике являются важным инструментом для создания и анимации объектов. Они позволяют визуализировать и передать информацию с помощью графических элементов, создавая эффекты и впечатления для пользователя.