Что такое диаметр в математике
Содержимое
- 1 Что такое диаметр в математике
Диаметр в математике — это расстояние, измеряемое вдоль окружности или сферы, проходящее через ее центр и соединяющее две точки на ее поверхности. Узнайте, как вычислить диаметр и его свойства в математике.
Диаметр — это один из основных понятий в математике, которое используется для измерения расстояния между двумя точками на окружности или сфере. Он является линейным отрезком, соединяющим две противоположные точки на окружности или сфере.
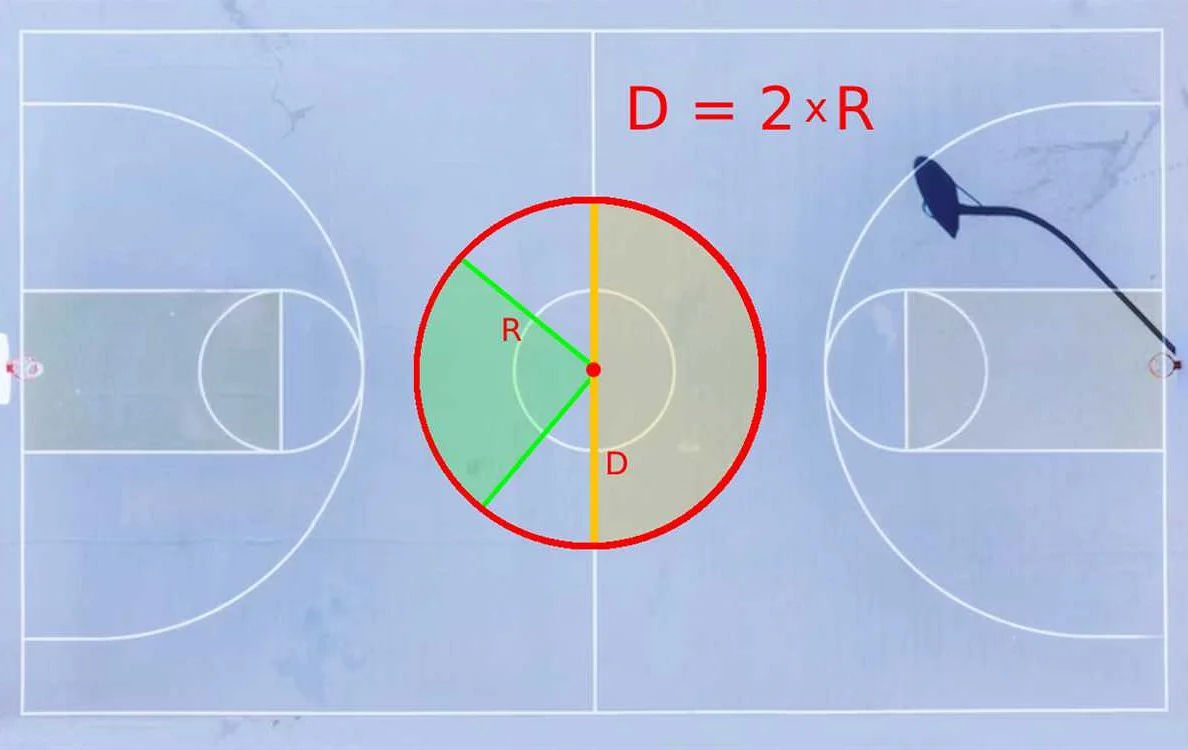
Диаметр обычно обозначается буквой «d» и является удвоенным радиусом окружности или половиной длины окружности. В математике диаметр также может быть определен как наибольшее расстояние между двумя точками на геометрической фигуре.
Например, если радиус окружности равен 5 см, то диаметр будет равен 10 см. То есть диаметр в два раза больше радиуса.
Диаметр широко используется в различных областях математики и науки, таких как геометрия, астрономия, физика и инженерия. Знание диаметра позволяет проводить различные вычисления, например, находить площадь и объем фигур, а также определять расстояния и размеры объектов.
Диаметр в математике: определение и примеры
Для круга, диаметр — это отрезок, соединяющий две точки на окружности и проходящий через ее центр. Длина диаметра равна удвоенному радиусу круга. Например, если радиус круга равен 5 см, то его диаметр будет равен 10 см.
Также диаметр можно определить для эллипса. В этом случае диаметр называется главной осью эллипса и представляет собой отрезок, проходящий через центр эллипса и соединяющий два самых удаленных друг от друга точки на его границе.
Важно отметить, что диаметр может быть определен не только для плоских фигур, но и для трехмерных объектов, таких как сфера. В этом случае диаметр — это отрезок, проходящий через центр сферы и соединяющий две точки на ее поверхности, наиболее удаленные друг от друга.
Диаметр имеет важное значение при решении различных геометрических задач. Например, для нахождения площади круга необходимо знать его диаметр или радиус. Также диаметр используется при вычислении объема и площади трехмерных объектов.
В заключение, диаметр — это величина, определяющая максимальное расстояние между двумя точками на геометрической фигуре. Он широко используется в математике для описания кругов, эллипсов, сфер и других геометрических объектов.
Что такое диаметр в математике?
Диаметр широко используется в различных областях математики, включая геометрию, топологию и анализ. Например, в геометрии диаметр окружности равен длине отрезка, проходящего через центр окружности и соединяющего две противоположные точки на ее границе.
Диаметр также может быть определен для других геометрических фигур, таких как эллипс, прямоугольник, треугольник и т.д. В каждом случае диаметр будет иметь свои уникальные свойства и значения.
Например, в прямоугольнике диаметр — это длина диагонали, соединяющей две противоположные вершины прямоугольника. В треугольнике диаметр может быть определен как длина отрезка, соединяющего две противоположные вершины треугольника, а также проходящего через его центр.
ФигураДиаметр
| Окружность | Длина отрезка, соединяющего две точки на границе окружности |
| Прямоугольник | Длина диагонали, соединяющей две противоположные вершины прямоугольника |
| Треугольник | Длина отрезка, соединяющего две противоположные вершины треугольника |
Знание диаметра позволяет получить информацию о размере и форме геометрической фигуры и использовать ее в различных математических задачах и рассуждениях. Поэтому понимание диаметра и его свойств является важным элементом в математике.
Определение диаметра
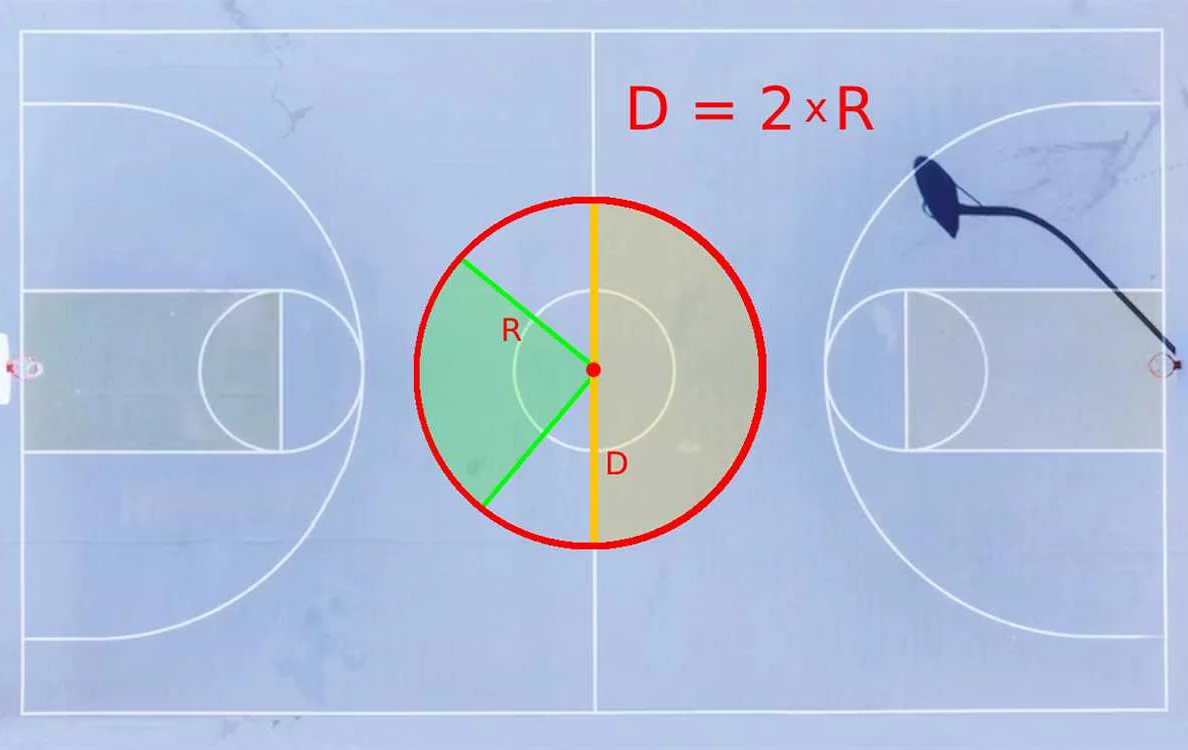
Чтобы найти диаметр фигуры, необходимо найти две точки на ее границе, через которые проходит отрезок, и провести его через центр фигуры. Например, для окружности диаметром будет отрезок, соединяющий две точки на ее границе и проходящий через ее центр.
Диаметр имеет большое значение в геометрии и используется в различных математических формулах и задачах. Он позволяет найти радиус фигуры, площадь и объем, а также решать задачи связанные с вписыванием и описыванием фигур вокруг других фигур.
Свойства диаметра
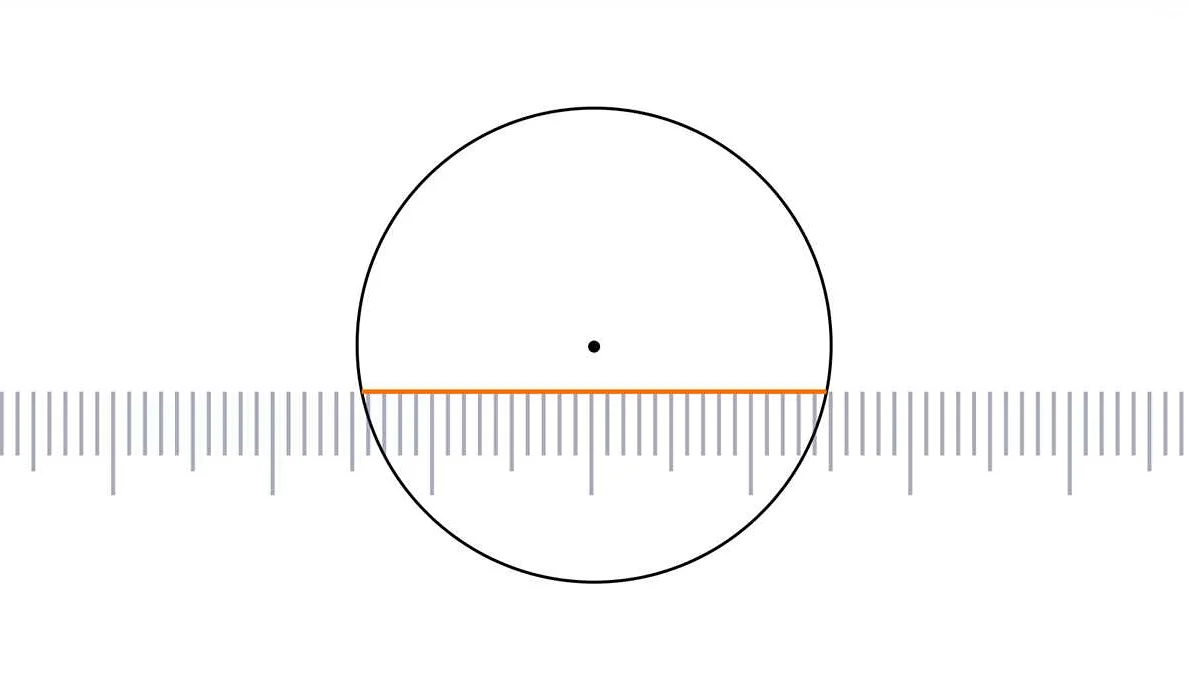
Вот несколько основных свойств диаметра:
- Диаметр является отрезком, соединяющим две противоположные точки на фигуре. Он всегда проходит через центр фигуры.
- Диаметр делит фигуру на две равные половины — симметричные относительно центра.
- Диаметр окружности является наибольшим возможным диаметром фигуры, так как окружность — это фигура с наименьшей площадью.
- Диаметр эллипса является наибольшей возможной прямой, соединяющей две точки на его границе.
- Диаметр прямоугольника совпадает с его длиной, если он вытянут вдоль одной из сторон.
Знание свойств диаметра является важным при решении различных геометрических задач и построении фигур.
Как найти диаметр?
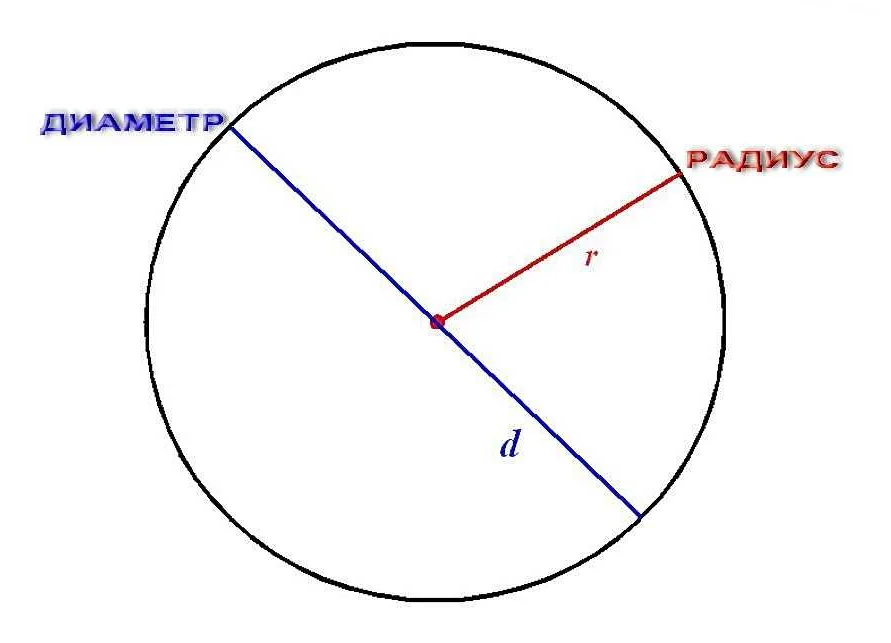
Существует несколько способов определения диаметра окружности:
1. Использование радиуса
Диаметр окружности можно найти, зная ее радиус (расстояние от центра окружности до любой ее точки). Диаметр равен удвоенному значению радиуса:
Диаметр = 2 * Радиус
2. Использование длины окружности
Если известна длина окружности, то диаметр можно найти, разделив длину на число π (пи):
Диаметр = Длина окружности / π
3. Использование координат
Для нахождения диаметра окружности по координатам двух ее точек можно воспользоваться формулой расстояния между двумя точками в пространстве:
Диаметр = √((x₂ — x₁)² + (y₂ — y₁)²)
Где (x₁, y₁) и (x₂, y₂) – координаты точек, через которые проходит диаметр.
Зная диаметр окружности, можно вычислить и другие важные параметры, такие как площадь и периметр окружности.
Примеры нахождения диаметра
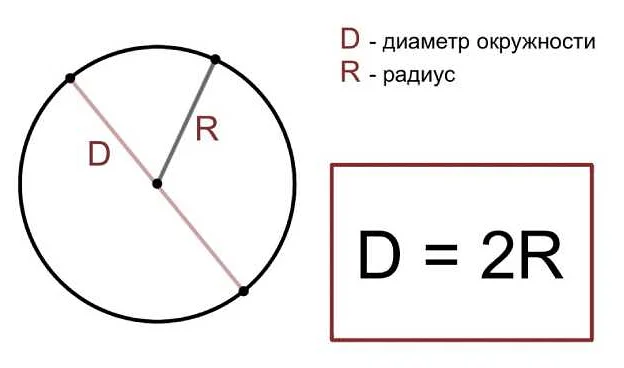
Ниже приведены примеры нахождения диаметра в различных геометрических фигурах:
- Пример 1: Найдем диаметр окружности. Диаметр окружности — это отрезок, соединяющий две точки на окружности и проходящий через центр окружности. Для нахождения диаметра окружности достаточно удвоить радиус. Например, если радиус окружности равен 5 см, то диаметр будет равен 10 см.
- Пример 2: Найдем диаметр сферы. Диаметр сферы — это отрезок, проходящий через центр сферы и имеющий концы на поверхности сферы. Для нахождения диаметра сферы достаточно удвоить радиус. Например, если радиус сферы равен 3 см, то диаметр будет равен 6 см.
- Пример 3: Найдем диаметр отрезка. Диаметр отрезка — это длина самого большого отрезка, который можно провести на данной прямой. Для нахождения диаметра отрезка необходимо измерить его длину. Например, длина отрезка AB равна 8 см, то диаметр будет равен 8 см.
Диаметр в геометрии
Диаметр является наибольшим отрезком, который можно провести внутри фигуры, и в случае с окружностью, он делит ее на две равные половины, называемые диаметральными отрезками.
Длина диаметра является ключевым параметром для определения площади и периметра окружности. Она также позволяет вычислить другие важные характеристики, такие как радиус и длина окружности.
Например, если длина диаметра окружности равна 10 см, то радиус окружности будет равен 5 см, а длина окружности составит 31,4 см (примерно 3,14 раза длиннее диаметра).
Диаметр также играет важную роль в других геометрических фигурах, таких как сфера и цилиндр. В этих случаях, диаметр позволяет определить объем и площадь поверхности данных фигур.
Диаметр в графах
Диаметр графа определяется как наибольшая длина среди всех кратчайших путей между всеми возможными парами вершин в графе. То есть диаметр показывает, насколько далеко друг от друга могут находиться различные вершины графа.
Диаметр графа может быть положительным числом, если в графе существуют вершины, между которыми существует путь, или же равно бесконечности, если граф является несвязным.
Для определения диаметра графа необходимо пройти по всем парам вершин и найти кратчайший путь между ними. Это можно сделать с помощью алгоритма Флойда-Уоршелла или алгоритма Дейкстры, в зависимости от типа графа.
Пример: рассмотрим граф с 6 вершинами и следующими ребрами: A-B, B-C, B-D, C-E, D-E, E-F. Для определения диаметра необходимо найти все кратчайшие пути между всеми парами вершин:
- А — F: длина пути = 5
- А — E: длина пути = 4
- А — D: длина пути = 3
- А — C: длина пути = 3
- А — B: длина пути = 1
- B — F: длина пути = 4
- B — E: длина пути = 3
- B — D: длина пути = 2
- B — C: длина пути = 2
- C — F: длина пути = 3
- C — E: длина пути = 2
- C — D: длина пути = 3
- D — F: длина пути = 2
- D — E: длина пути = 1
- E — F: длина пути = 1
Таким образом, диаметр данного графа равен 5, так как наибольшая длина пути между всеми парами вершин равна 5.
Вопрос-ответ:
Что такое диаметр в математике?
В математике диаметр — это отрезок, соединяющий две точки на окружности или на сфере и проходящий через её центр. Диаметр является наибольшим возможным отрезком, который может быть проведен через данную фигуру.
Можно ли измерить диаметр окружности?
Да, диаметр окружности может быть измерен. Для этого необходимо провести отрезок, соединяющий две точки на окружности и проходящий через её центр. Длина этого отрезка и будет являться диаметром.
Какие еще фигуры имеют диаметр?
В дополнение к окружностям, диаметром также обладают сферы и некоторые другие геометрические фигуры. Например, в сфере диаметром является отрезок, соединяющий две точки на поверхности сферы и проходящий через её центр.
Как диаметр связан с радиусом окружности?
Диаметр окружности в два раза больше радиуса. Или, другими словами, радиус окружности равен половине её диаметра. Если известен диаметр окружности, то радиус можно найти, разделив диаметр на 2. Если известен радиус, то диаметр можно найти, умножив радиус на 2.
Вывод

Диаметр является важной характеристикой для измерения размеров и свойств геометрических фигур. Он используется в различных областях математики, физики, инженерии и других наук. Знание диаметра помогает в решении задач, связанных с конструкцией, измерением и анализом объектов.
Примеры применения диаметра включают определение размеров колеса у транспортных средств, расчет длины отрезка на окружности, определение геометрических параметров сферических объектов и другие задачи, где требуется измерить наибольшее расстояние между двумя точками на кривой или поверхности.


Статья очень понравилась! Я всегда была любознательна по отношению к математике, и это объяснение дало мне новые знания о диаметре. Теперь я понимаю, что диаметр — это отрезок, соединяющий две точки на окружности и проходящий через ее центр. Это важное понятие в геометрии и имеет много применений в реальной жизни. Примеры, которые были приведены в статье, также были очень полезными. Я посмотрела на рулон ленты и увидела, что его диаметр — это расстояние между самыми удаленными точками на краях ленты. Теперь я понимаю, что диаметр может быть измерен на любом круглом объекте, будь то шар, бутылка или колесо. Статья была написана очень понятно и легко читалась. Я ценю примеры и иллюстрации, которые помогают визуализировать понятие диаметра. Они действительно помогли мне лучше понять материал. В целом, статья дала мне полное представление о диаметре в математике. Я теперь могу использовать этот термин с уверенностью и пониманием его значения. Я надеюсь, что автор продолжит делиться своими знаниями и объяснениями в других математических темах. Спасибо!
Диаметр в математике — это геометрическая характеристика фигуры, которая определяется как наибольшее расстояние между двумя точками этой фигуры. В зависимости от типа фигуры, диаметр может иметь различные определения и свойства. Например, в случае окружности, диаметр — это отрезок, соединяющий две противоположные точки окружности, и он является наибольшим из всех возможных отрезков, проведенных внутри окружности. В треугольнике, диаметр может быть определен как отрезок, соединяющий две вершины, не лежащие на одной стороне треугольника. Этот отрезок проходит через центр описанной окружности треугольника и также является наибольшим возможным отрезком внутри треугольника. Диаметр также может быть использован для определения других геометрических величин, таких как радиус, площадь и объем. Например, радиус окружности можно найти, разделив диаметр на два. В математике диаметр играет важную роль при решении различных задач, связанных с геометрией и определением характеристик фигур. Поэтому понимание этого понятия является необходимым для успешного изучения математики.