Что такое сфера по математике

Сфера в математике — это трехмерное геометрическое тело, которое ограничено поверхностью, состоящей из всех точек, находящихся на постоянном расстоянии от центра. Сфера является одним из основных объектов изучения в геометрии и имеет много применений в различных областях науки и техники.

Сфера — это основная геометрическая фигура, которая обладает множеством интересных свойств и находит широкое применение в различных областях науки и техники. В математике сфера представляет собой трехмерный геометрический объект, состоящий из всех точек в пространстве, равноудаленных от центра этой фигуры. Сфера обладает множеством уникальных свойств и является одной из наиболее изученных и известных геометрических фигур.

Основные характеристики сферы:

1. Центр – точка, равноудаленная от всех точек на поверхности сферы.

2. Радиус – расстояние от центра сферы до любой точки на ее поверхности.

3. Диаметр – удвоенное значение радиуса, то есть отрезок, соединяющий две точки на поверхности сферы и проходящий через ее центр.

4. Поверхность – сфера представляет собой гладкую и закрытую поверхность, которая разделена на бесконечное число маленьких фрагментов – сферических треугольников.

5. Объем – количество трехмерного пространства, ограниченного сферой.

Примерами применения сфер в реальной жизни могут служить геодезия при измерении земного шара, астрономия при моделировании планет или звезд, а также медицина при исследовании формы органов человеческого тела. Знание основных свойств сферы позволяет математикам и инженерам решать сложные задачи, связанные с проектированием, измерением и моделированием трехмерных объектов.

Определение сферы в математике

Сфера является трехмерным аналогом окружности в плоскости. Она представляет собой поверхность, равноудаленную от центра. В математике сферу обозначают символом S или с помощью уравнения вида (x — a)^2 + (y — b)^2 + (z — c)^2 = R^2, где (a, b, c) — координаты центра сферы, а R — радиус.

Сферы встречаются в различных областях математики и физики. Они широко применяются при решении задач в геометрии, а также в компьютерной графике и моделировании.

Примеры сфер в реальном мире включают в себя планеты, молекулы, шары для спорта, а также множество других объектов, которые имеют форму сферы или приближенно к ней.

Геометрические свойства сферы

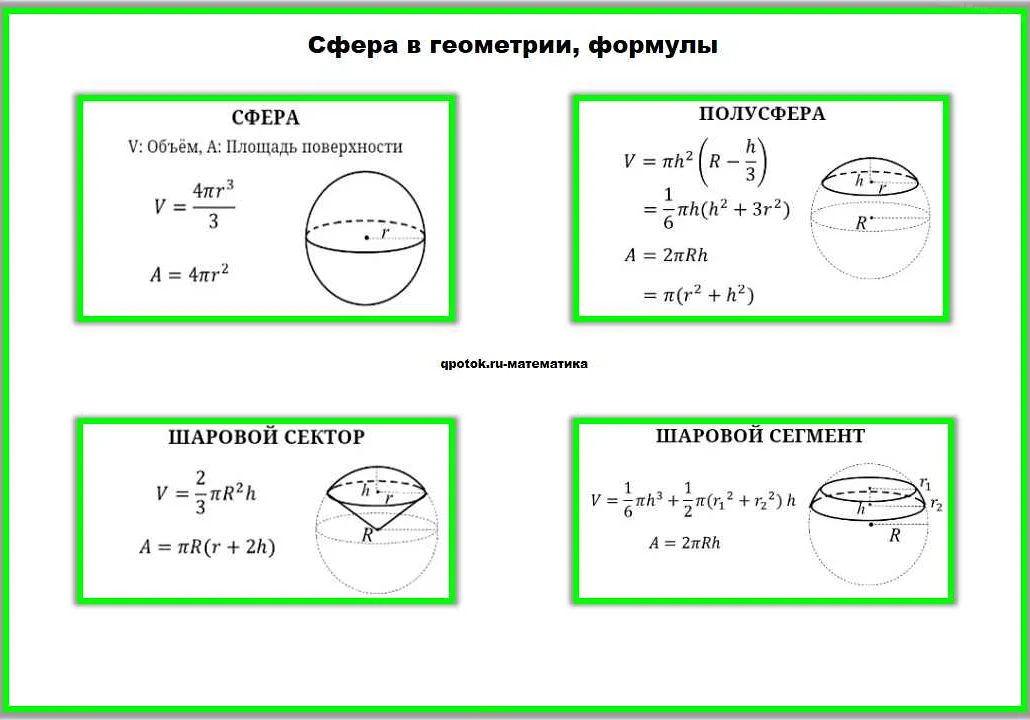
1. Диаметр сферы. Диаметром сферы называется отрезок, соединяющий две противоположные точки её поверхности, проходящие через центр. Диаметр является максимальной прямой линией, которая может быть проведена на поверхности сферы.

2. Радиус сферы. Радиусом сферы называется отрезок, соединяющий центр сферы и любую точку её поверхности. Радиус является половиной диаметра и определяет расстояние от центра сферы до её поверхности.

3. Площадь поверхности сферы. Площадь поверхности сферы вычисляется по формуле: S = 4πR², где S – площадь поверхности, R – радиус сферы. Площадь поверхности сферы является показателем её площади и увеличивается с увеличением радиуса.

4. Объём сферы. Объём сферы вычисляется по формуле: V = (4/3)πR³, где V – объём сферы, R – радиус сферы. Объём сферы является показателем её вместимости и увеличивается с увеличением радиуса.

5. Геометрические связи. Сфера имеет геометрические связи с другими геометрическими фигурами, такими как плоскость (сфера может быть вписана в плоскость или пересекать её), цилиндр (сфера может быть вписана в цилиндр или описана вокруг его боковой поверхности), конус (сфера может быть вписана в конус или описана вокруг его боковой поверхности).

Изучение геометрических свойств сферы является важным элементом в математике и находит применение в различных областях науки и техники, таких как астрономия, физика, строительство и дизайн.

Площадь поверхности сферы

S = 4πr²,

где S — площадь поверхности сферы, а r — радиус сферы.

Формула была получена с помощью интегрирования и представляет собой упрощенную формулу для определения площади сферы.

Например, если радиус сферы равен 5 см, то площадь поверхности сферы будет:

S = 4π(5)² = 4π(25) ≈ 314.16 см².

Таким образом, площадь поверхности сферы равна приблизительно 314.16 см² для сферы с радиусом 5 см.

Объем сферы

Чтобы найти объем сферы, можно использовать следующую формулу:

V = (4/3)πr³

где V — объем сферы, π — число π (пи), r — радиус сферы.

Формула для объема сферы основана на том факте, что сфера является трехмерным аналогом круга. Радиус сферы — это расстояние от центра сферы до любой ее точки. Число π — это математическая константа, которая приближенно равна 3,14159 и используется для вычисления длины окружности и площади круга.

Например, пусть радиус сферы равен 5 см. Тогда, используя формулу для объема сферы, можно найти ее объем:

V = (4/3)π(5³) = (4/3)π(125) ≈ 523,6 см³

Таким образом, объем сферы с радиусом 5 см составляет приблизительно 523,6 кубических сантиметра.

Знание формулы для объема сферы позволяет решать различные задачи, связанные с геометрией и физикой. Например, объем сферы может использоваться для определения объема шарообразных объектов, таких как шары, пузыри или капли жидкости.

Уравнение сферы

Уравнение сферы имеет следующий вид:

x2 + y2 + z2

=

r2

Где (x, y, z) — координаты точки на поверхности сферы, а r — радиус сферы.

Уравнение сферы можно использовать для определения расстояния между точками на сфере. Если в уравнение подставить значения координат двух точек, то получится неравенство, истинность которого будет означать, что эти точки находятся на одной сфере.

Например, уравнение сферы с центром в точке (0, 0, 0) и радиусом 5 будет иметь вид:

x2 + y2 + z2

=

25

Таким образом, все точки (x, y, z), которые удовлетворяют этому уравнению, лежат на поверхности сферы с радиусом 5 и центром в начале координат.

Видео по теме:

Вопрос-ответ:

Как определить сферу по математике?

Сфера в математике определяется как множество точек, равноудаленных от данной фиксированной точки, называемой центром сферы. Формально, сфера — это геометрическое место точек в трехмерном пространстве, расстояние от которых до центра сферы равно заданному радиусу.

Какие свойства имеет сфера?

Сфера имеет несколько важных свойств. Во-первых, все точки на сфере равноудалены от центра, поэтому радиус сферы одинаков для всех точек на ней. Во-вторых, сфера не имеет начала и конца, она бесконечна во всех направлениях. В-третьих, сфера является закрытой поверхностью без края.

Какие примеры сфер встречаются в математике и реальной жизни?

Сферы встречаются во множестве задач и ситуаций. Некоторые примеры сфер из реальной жизни включают: Земля (которая приближенно является сферой), мячи различных видов, шары для боулинга и бильярда, а также множество других предметов и конструкций, имеющих округлую форму.

Каковы основные формулы и уравнения, связанные со сферой?

Основные формулы, связанные со сферой, включают: формулу объема сферы (V = (4/3)πr³, где V — объем, π — число Пи, r — радиус сферы), формулу площади поверхности сферы (S = 4πr², где S — площадь поверхности сферы), а также уравнение сферы ((x — a)² + (y — b)² + (z — c)² = r², где (a, b, c) — координаты центра сферы).

Сферические координаты

Радиус (r) представляет собой расстояние от начала координат до точки на сфере. Полярный угол (θ) измеряется от положительной оси z и определяет угол между радиусом и положительной осью z. Азимутальный угол (φ) измеряется от положительной оси x и определяет угол между проекцией радиуса на плоскость xy и положительной осью x.

Сферические координаты могут быть полезны при решении задач, связанных с сферическими объектами, такими как планеты, атмосферы, а также в физике, геодезии и астрономии.

Пример использования сферических координат: рассмотрим точку на поверхности Земли. Радиус (r) будет равен радиусу Земли. Полярный угол (θ) будет определять широту точки, а азимутальный угол (φ) — долготу точки.

Примеры задач с использованием сферы

Пример 1: Найдите объем сферы с радиусом 5 см.

Решение: Формула для вычисления объема сферы: V = (4/3)πr³, где r — радиус сферы. Подставляя значение радиуса, получим:

V = (4/3)π(5 см)³ = (4/3)π125 см³ ≈ 523.6 см³

Ответ: Объем сферы равен примерно 523.6 см³.

Пример 2: Найдите площадь поверхности сферы с радиусом 2 м.

Решение: Формула для вычисления площади поверхности сферы: S = 4πr², где r — радиус сферы. Подставляя значение радиуса, получим:

S = 4π(2 м)² = 4π4 м² = 16π м² ≈ 50.27 м²

Ответ: Площадь поверхности сферы равна примерно 50.27 м².

Пример 3: Найдите длину окружности сечения сферы, если радиус сферы равен 3 см.

Решение: Сечение сферы плоскостью является окружностью. Длина окружности можно найти по формуле: L = 2πr, где r — радиус окружности. Подставляя значение радиуса сферы, получим:

L = 2π(3 см) = 6π см ≈ 18.85 см

Ответ: Длина окружности сечения сферы равна примерно 18.85 см.

Это лишь некоторые примеры задач, где можно применить знания о сфере. Сфера имеет множество свойств и применений, и она является основой для изучения более сложных геометрических фигур и математических концепций.