Что такое диффуры в математике
Содержимое
- 1 Что такое диффуры в математике
- 1.1 Что такое дифференциальное уравнение?
- 1.2 Основные понятия
- 1.3 Типы дифференциальных уравнений
- 1.4 Линейные дифференциальные уравнения
- 1.5 Нелинейные дифференциальные уравнения
- 1.6 Видео по теме:
- 1.7 Вопрос-ответ:
- 1.7.0.1 Что такое дифференциальные уравнения?
- 1.7.0.2 Какие основные понятия связаны с дифференциальными уравнениями?
- 1.7.0.3 Можете привести пример дифференциального уравнения?
- 1.7.0.4 Как решаются дифференциальные уравнения?
- 1.7.0.5 В каких областях науки применяются дифференциальные уравнения?
- 1.7.0.6 Что такое дифференциальное уравнение?
- 1.7.0.7 Какие бывают виды дифференциальных уравнений?
- 1.8 Примеры дифференциальных уравнений
- 1.9 Практическое применение дифференциальных уравнений
Статья расскажет о дифференциальных уравнениях и их использовании в математике. Узнайте, как они помогают описывать изменение величин во времени и пространстве и какие методы решения применяются для поиска их решений.
Дифференциальные уравнения – это важный раздел математики, который изучает зависимости между функциями и их производными. Они находят широкое применение в физике, экономике, биологии и других областях науки.
Основным понятием в дифференциальных уравнениях является производная. Производная функции показывает, как меняется значение функции при изменении аргумента. Дифференциальные уравнения описывают связь между производными функций и сами функции.
Примером дифференциального уравнения может служить простейшее уравнение вида:
y’ = kx
Здесь y – это функция, которую нужно найти, x – аргумент функции, а k – постоянная. Уравнение показывает, что производная функции y по x равна произведению постоянной k на значение x.
Изучение дифференциальных уравнений позволяет решать задачи, связанные с изменением величин во времени или пространстве. Они помогают предсказывать траектории движения тел, моделировать экономические процессы и анализировать изменения в биологических системах. Понимание основных понятий и примеров дифференциальных уравнений является важным для успешного применения их в различных областях науки и техники.
Что такое дифференциальное уравнение?
f(x, y, y’, y», …, y(n)) = 0,
где x – независимая переменная, y(x) – искомая функция, а y’, y», …, y(n) – ее производные до n-го порядка.
Дифференциальные уравнения широко используются в математике, физике, экономике и других науках для описания различных процессов и явлений. Они позволяют моделировать изменение величин и находить аналитические решения, что делает их мощным инструментом в исследовании природы и ее явлений.
Дифференциальные уравнения могут быть разделены на различные типы в зависимости от их видов и свойств. Одним из наиболее распространенных типов являются обыкновенные дифференциальные уравнения, которые описывают функцию одной переменной. Также существуют частные дифференциальные уравнения, описывающие функции нескольких переменных.
Решение дифференциального уравнения состоит в нахождении функции y(x), которая удовлетворяет уравнению. Решение может быть найдено аналитически или численно при помощи различных методов, таких как метод разделения переменных, метод вариации постоянных, метод интегральных множителей и другие.
Дифференциальные уравнения играют важную роль в науке и технике, являясь основой для различных теорий и моделей. Они позволяют описывать и предсказывать поведение систем и процессов, а также находить оптимальные решения в различных задачах.
Основные понятия
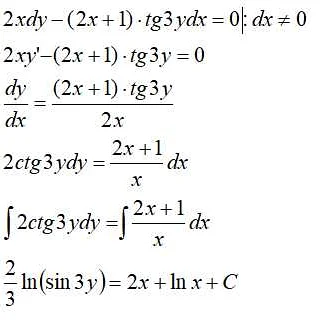
Обыкновенное дифференциальное уравнение (ОДУ) – это дифференциальное уравнение, которое содержит только одну неизвестную функцию и ее производные по одной переменной.
Частное дифференциальное уравнение (ЧДУ) – это дифференциальное уравнение, которое содержит несколько неизвестных функций и их производные по нескольким переменным.
Интеграл дифференциального уравнения – это функция, которая удовлетворяет исходному уравнению, после его дифференцирования и интегрирования.
Начальное условие – это условие, заданное для неизвестной функции и ее производной, при заданном значении аргумента. Оно позволяет найти единственное решение дифференциального уравнения.
Граничное условие – это условие, заданное для неизвестной функции и ее производной, при заданных значениях аргумента на границе области определения. Оно позволяет найти решение дифференциального уравнения среди множества возможных решений.
Аналитическое решение – это решение дифференциального уравнения, которое можно выразить в явном виде с помощью элементарных функций, констант и операций.
Численное решение – это приближенное решение дифференциального уравнения, полученное с использованием численных методов, таких как метод Эйлера или метод Рунге-Кутты.
Линейное дифференциальное уравнение – это дифференциальное уравнение, которое содержит только линейные функции и их производные. Одно из основных свойств линейных дифференциальных уравнений – принцип суперпозиции.
Нелинейное дифференциальное уравнение – это дифференциальное уравнение, которое содержит нелинейные функции или их производные. Одно из основных свойств нелинейных дифференциальных уравнений – их возможность моделировать сложные физические и биологические процессы.
Стационарное решение – это решение дифференциального уравнения, которое не зависит от времени и остается неизменным на протяжении всего процесса.
Устойчивое решение – это решение дифференциального уравнения, которое при небольших изменениях начальных условий или параметров системы остается близким к исходному решению.
Типы дифференциальных уравнений

В зависимости от типа функции, дифференциальные уравнения могут быть:
- Обыкновенными дифференциальными уравнениями (ОДУ): это уравнения, в которых присутствуют только обыкновенные производные, то есть производные по одной или нескольким переменным. Примеры ОДУ: y» + y’ + y = 0, y’ = 2xy.
- Частными дифференциальными уравнениями (ЧДУ): это уравнения, в которых присутствуют частные производные, то есть производные по нескольким переменным. Частные дифференциальные уравнения являются более сложными, чем обыкновенные, и находят применение в физике и математической физике. Примеры ЧДУ: уравнение теплопроводности, уравнение Лапласа.
Также дифференциальные уравнения можно классифицировать по порядку, линейности, степени и другим параметрам, что позволяет более точно определить и изучить их свойства и решения.
Различные типы дифференциальных уравнений имеют свои особенности и методы решения. Изучение типов дифференциальных уравнений является важным шагом в изучении этой области математики и находит применение во многих прикладных областях, включая физику, экономику и инженерные науки.
Линейные дифференциальные уравнения
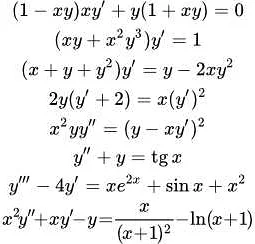
Общий вид линейного дифференциального уравнения первого порядка можно записать следующим образом:
a(x) * y'(x) + b(x) * y(x) = c(x),
где y(x) — неизвестная функция, y'(x) — ее производная по переменной x, а a(x), b(x) и c(x) — линейные функции от x.
Решение линейного дифференциального уравнения осуществляется посредством нахождения такой функции y(x), которая удовлетворяет уравнению при всех значениях переменной x в заданной области.
Примеры линейных дифференциальных уравнений включают уравнение экспоненциального роста, уравнение испытывающее затухание и уравнение колебаний со сдвигом. Решение таких уравнений позволяет моделировать и анализировать различные физические и инженерные системы.
Примеры линейных дифференциальных уравнений:
1. Уравнение экспоненциального роста:
y'(x) = k * y(x),
где k — постоянная.
2. Уравнение испытывающее затухание:
y'(x) + a * y(x) = 0,
где a — постоянная.
3. Уравнение колебаний со сдвигом:
y»(x) + b * y'(x) + c * y(x) = 0,
где b и c — постоянные.
Нелинейные дифференциальные уравнения
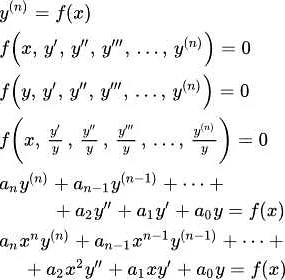
Дифференциальные уравнения, в которых функции и их производные входят нелинейно, называются нелинейными дифференциальными уравнениями. Они представляют собой более сложный класс уравнений, чем линейные дифференциальные уравнения.
В нелинейных дифференциальных уравнениях нелинейность может проявляться в различных формах, таких как умножение функций, возведение в степень, использование функций с нелинейной зависимостью и т. д. Нелинейные дифференциальные уравнения могут иметь множество решений или не иметь их вовсе.
Решение нелинейных дифференциальных уравнений является сложной задачей и требует применения различных методов и техник. В отличие от линейных дифференциальных уравнений, для которых существуют общие методы решения, нелинейные уравнения требуют индивидуального подхода и анализа конкретной задачи.
Примером нелинейного дифференциального уравнения может служить уравнение Лотки-Вольтерры, которое описывает взаимодействие хищников и жертв в биологической системе. Другим примером может быть уравнение Ньютона для движения тела под действием силы сопротивления воздуха.
Видео по теме:
Вопрос-ответ:
Что такое дифференциальные уравнения?
Дифференциальные уравнения – это уравнения, которые связывают неизвестную функцию с ее производными. Они широко используются в математике, физике, экономике и других науках для описания изменения каких-либо величин в зависимости от других переменных.
Какие основные понятия связаны с дифференциальными уравнениями?
Основными понятиями, связанными с дифференциальными уравнениями, являются производная функции, общее решение дифференциального уравнения, частное решение дифференциального уравнения, начальные условия, граничные условия.
Можете привести пример дифференциального уравнения?
Один из примеров дифференциального уравнения – уравнение вида dy/dx = x^2, где y – неизвестная функция, а x – независимая переменная. Это уравнение описывает изменение функции y в зависимости от переменной x.
Как решаются дифференциальные уравнения?
Дифференциальные уравнения решаются путем нахождения общего решения, которое удовлетворяет уравнению при любых значениях переменных, и частного решения, которое удовлетворяет уравнению только при заданных начальных или граничных условиях.
В каких областях науки применяются дифференциальные уравнения?
Дифференциальные уравнения широко применяются в физике для описания движения тел, электромагнитных полей и других физических явлений. Они также используются в экономике для моделирования экономических процессов и в других науках для анализа изменения различных величин.
Что такое дифференциальное уравнение?
Дифференциальное уравнение — это уравнение, в котором неизвестной функцией является функция, а вместо обычной алгебраической операции используются дифференциальные операции. Оно описывает зависимость искомой функции от ее производных.
Какие бывают виды дифференциальных уравнений?
Существует несколько видов дифференциальных уравнений, включая обыкновенные дифференциальные уравнения, частные дифференциальные уравнения, линейные и нелинейные дифференциальные уравнения, стационарные и нестационарные дифференциальные уравнения.
Примеры дифференциальных уравнений
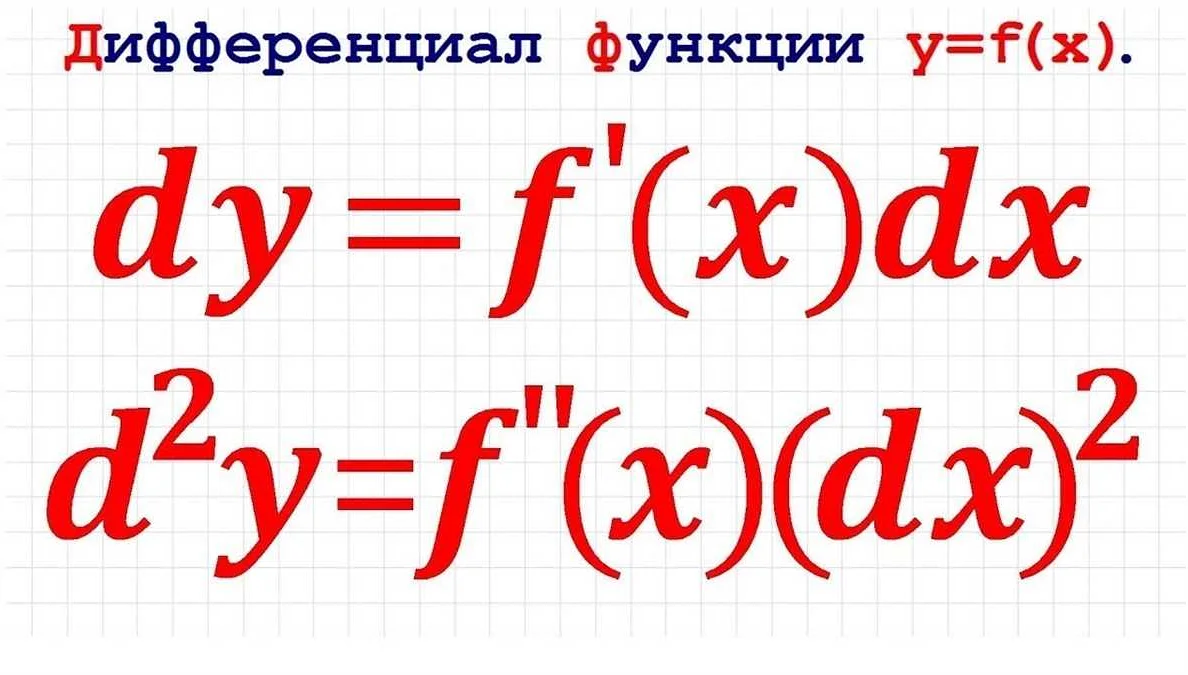
Линейное дифференциальное уравнение первого порядка:
$$\frac{dy}{dx} + 2xy = x$$
Это уравнение описывает зависимость функции $$y(x)$$ от переменной $$x$$. Здесь $$\frac{dy}{dx}$$ — производная функции $$y$$ по переменной $$x$$. Решение этого уравнения может быть найдено с помощью метода вариации постоянной или метода Лагранжа.
Дифференциальное уравнение второго порядка:
$$\frac{d^2y}{dx^2} + 4y = 0$$
Это уравнение описывает колебания гармонического осциллятора. Решение этого уравнения можно найти с помощью метода характеристического уравнения или методом разделяющихся переменных.
Дифференциальное уравнение с частными производными:
$$\frac{\partial^2u}{\partial t^2} — c^2\frac{\partial^2u}{\partial x^2} = 0$$
Это уравнение описывает распространение волн на струне или другой упругой среде. Здесь $$u(x, t)$$ — функция зависящая от переменных $$x$$ и $$t$$. Решение этого уравнения можно найти с помощью метода разделения переменных или метода Фурье.
Практическое применение дифференциальных уравнений
Дифференциальные уравнения имеют широкое практическое применение в различных областях науки и техники. Они помогают моделировать и описывать различные физические, химические, биологические, экономические и инженерные процессы.
Одной из наиболее распространенных областей применения дифференциальных уравнений является физика. С их помощью можно описать движение тел, электромагнитные поля, теплопроводность, распространение звука и многое другое. Например, уравнение Ньютона для описания движения тела является дифференциальным уравнением второго порядка.
В химии дифференциальные уравнения используются для описания кинетики химических реакций. Они позволяют определить скорость реакции и изменение концентрации веществ во времени. Также они применяются при моделировании химических реакторов и процессов очистки воды.
Биология использует дифференциальные уравнения для моделирования динамики популяций, роста организмов, распространения заболеваний и других биологических процессов. Например, уравнение Лотки-Вольтерры описывает взаимодействие хищников и жертв в экосистеме.
В экономике дифференциальные уравнения применяются для моделирования экономических процессов, таких как инфляция, безработица, рост населения и другие. Они позволяют предсказывать изменение показателей экономики и разрабатывать стратегии управления.
Также дифференциальные уравнения применяются в инженерии для моделирования и проектирования различных систем и процессов. Они используются в механике, электротехнике, теплотехнике, автоматическом управлении и других областях. Например, уравнения Навье-Стокса описывают движение жидкости или газа.
Практическое применение дифференциальных уравнений включает разработку математических моделей, решение этих уравнений и анализ полученных решений. Оно позволяет получить информацию о поведении системы во времени и принять соответствующие решения или предсказания.
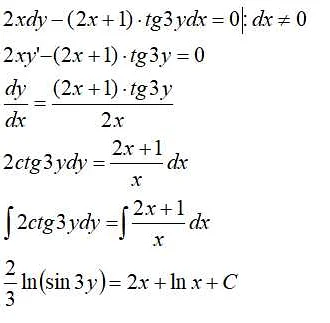



Статья очень интересная и понятная. Я давно интересуюсь математикой, но дифференциальные уравнения всегда казались мне сложными. Но благодаря этому материалу я поняла, что они вовсе не такие уж и страшные. Очень понравилось, что автор начинает с объяснения основных понятий, таких как производная и интеграл, чтобы мы могли лучше понять суть дифференциальных уравнений. Примеры, которые приведены в статье, также очень помогли мне разобраться в теме. Автор очень доступно и подробно объясняет каждый шаг, что позволяет понять, как именно решать дифференциальные уравнения. Теперь у меня появилось желание попробовать решить такое уравнение самостоятельно. Спасибо за информативную и познавательную статью!