Что такое производная простыми словами в математике
Содержимое
- 1 Что такое производная простыми словами в математике
- 1.1 Определение и основные понятия
- 1.2 Формула и геометрическая интерпретация
- 1.3 Основные правила дифференцирования
- 1.4 Примеры применения производной
- 1.5 Производная и скорость изменения
- 1.6 Производная и экстремумы функций
- 1.7 Производная и график функции
- 1.8 Вопрос-ответ:
- 1.9 Производная и определенный интеграл
- 1.10 Видео по теме:
Производная — это понятие, которое позволяет измерить скорость изменения функции. В математике она вычисляется как предел отношения изменения функции к изменению ее аргумента. Понять производную можно, представив себе, что она показывает, насколько быстро функция меняется в каждой точке. Знание производной важно для понимания множества математических и естественных явлений.
Производная – это одно из ключевых понятий математического анализа. Простыми словами, производная показывает, как быстро меняется функция в каждой точке своего определения. Другими словами, она позволяет узнать, насколько функция «крутая» или «плоская» в каждой точке.
Но зачем нужно знать, как быстро меняется функция? Производная имеет множество практических применений. Например, она может помочь нам определить угол наклона касательной к графику функции в определенной точке. Это полезно при решении задач физики, экономики или механики.
Чтобы получить производную функции, нужно найти ее предел при стремлении приращения функции к нулю. Таким образом, производная показывает, как меняется функция, когда ее аргументы (входные значения) изменяются незначительно.
Производная – неотъемлемая часть дифференциального исчисления и является основой для многих математических методов и моделей. Она помогает нам понять и предсказать поведение функций, а также решать широкий спектр задач из разных областей знания.
Определение и основные понятия
Введем несколько основных понятий, чтобы лучше понять, что такое производная.
ТерминОписание
| Функция | Функция — это правило, которое сопоставляет каждому элементу из одного множества (называемого областью определения) элемент из другого множества (называемого областью значений). В контексте производной, функция описывает зависимость одной переменной от другой. |
| Предел | Предел — это математическое понятие, которое описывает поведение функции вблизи определенной точки. Предел функции определяется как значение, к которому стремится функция при приближении аргумента к определенной точке. |
| Инкремент | Инкремент — это приращение аргумента функции. В контексте производной, инкремент обозначается как Δx и представляет собой малое изменение аргумента. |
| Дифференциал | Дифференциал — это приращение функции, которое зависит от приращения аргумента и производной функции. Дифференциал обозначается как Δy и представляет собой малое изменение значения функции. |
Используя эти понятия, производная функции может быть определена как предел отношения дифференциала к инкременту аргумента при стремлении инкремента к нулю. Производная показывает скорость изменения функции в данной точке и может быть использована для определения экстремумов, тангенциальных прямых и других свойств функции.
Формула и геометрическая интерпретация

Производная функции в точке определяет скорость изменения этой функции в данной точке. Она показывает, как быстро значение функции меняется при изменении ее аргумента.
Формула производной позволяет найти точное значение производной функции в заданной точке. Для функции y = f(x) производная в точке x_0 обозначается как f'(x_0) или dy/dx|x=x_0. Она определяется как предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю:
| f'(x_0) = lim | (f(x) — f(x_0)) / (x — x_0) |
| x->x_0 | x->x_0 |
Геометрическая интерпретация производной заключается в том, что она представляет собой тангенс угла наклона касательной к графику функции в данной точке. Если функция увеличивается, то производная положительна; если функция убывает, то производная отрицательна; если функция не меняется, то производная равна нулю.
Основные правила дифференцирования
- Правило суммы: производная суммы двух функций равна сумме производных этих функций.
- Правило произведения: производная произведения двух функций равна произведению производной первой функции на вторую функцию, плюс произведение первой функции на производную второй функции.
- Правило деления: производная отношения двух функций равна разности произведения производной первой функции на вторую функцию и произведения первой функции на производную второй функции, деленной на квадрат второй функции.
- Правило цепной функции: производная сложной функции равна произведению производной внешней функции на производную внутренней функции.
Знание этих основных правил дифференцирования позволяет более легко находить производные сложных функций и решать задачи, связанные с изучением и применением производной.
Примеры применения производной
Одним из основных применений производной является нахождение скорости изменения величины. Например, если у нас есть функция, описывающая положение объекта в зависимости от времени, производная этой функции позволяет найти скорость движения объекта в каждый момент времени.
Еще одним примером применения производной является нахождение экстремумов функции. Производная позволяет определить точки, в которых функция имеет наибольшее или наименьшее значение. Это может быть полезно в оптимизации процессов или поиске наилучших решений.
Производная также используется для анализа графиков функций. Она позволяет определить точки перегиба, максимумы и минимумы функции, что помогает в изучении и понимании поведения функций.
Это лишь некоторые примеры применения производной. Она широко используется во многих областях знания и является важным инструментом для анализа и оптимизации процессов.
Производная и скорость изменения
Когда мы говорим о скорости изменения, мы обычно имеем в виду, насколько быстро меняется функция в определенной точке. Производная функции позволяет нам определить эту скорость изменения.
Математически, производная функции в точке определяется как предел отношения изменения функции к изменению аргумента при стремлении последнего к нулю. Иными словами, производная показывает, как функция меняется в зависимости от изменения ее аргумента.
Скорость изменения может быть положительной или отрицательной, в зависимости от направления изменения функции. Если производная положительна, это означает, что функция растет; если производная отрицательна, это означает, что функция убывает.
Производная также может быть равной нулю в определенных точках, что указывает на экстремумы функции — максимумы или минимумы. Это связано с тем, что в таких точках скорость изменения функции временно становится равной нулю.
Понимание производной и ее связи со скоростью изменения позволяет нам анализировать и предсказывать поведение функций в различных ситуациях. Это особенно полезно в физике, экономике, биологии и других областях, где мы сталкиваемся с изменениями величин и процессов.
Производная и экстремумы функций

Экстремум функции – это точка, в которой функция достигает наибольшего (максимум) или наименьшего (минимум) значения в заданной области. Они имеют важное значение в различных областях науки и применяются для решения различных практических задач.
Изучение экстремумов функции связано с анализом ее производной. Если производная в точке равна нулю, то это может означать, что в этой точке функция достигает экстремума. Однако, не все точки с нулевой производной являются точками экстремума. Например, может быть точка перегиба – точка, в которой меняется направление выпуклости функции.
Для определения типа экстремума используют вторую производную функции. Если вторая производная положительна, то это указывает на минимум, а если отрицательна – на максимум. В случае, когда вторая производная равна нулю, применяют дополнительные методы исследования.
Использование производной и изучение экстремумов функций позволяет решать разнообразные задачи, связанные с оптимизацией, определением экстремальных значений и нахождением критических точек. Это важное понятие в математике, физике, экономике и других науках.
Производная и график функции
Производная функции в каждой точке графика показывает, насколько быстро меняется значение функции в данной точке. Если производная положительна, то функция возрастает, если производная отрицательна — функция убывает. Момент, когда производная равна нулю, называется экстремумом функции.
Изменение знака производной позволяет определить, где функция возрастает или убывает. Если производная меняет знак с плюса на минус, то это означает, что на графике функции есть максимум. Если знак меняется с минуса на плюс, то на графике есть минимум. Если производная не меняет знак, то функция имеет горизонтальный экстремум.
Зная график функции, можно определить ее производную в каждой точке, а затем использовать это знание для определения ее поведения и свойств на всем промежутке. Производная является полезным инструментом для анализа функций и нахождения критических точек, экстремумов и точек перегиба.
Вопрос-ответ:
Зачем нужна производная?
Производная функции показывает, как быстро меняется значение функции по отношению к ее аргументу. Это позволяет найти точку экстремума, определить направление изменения функции и многое другое. В общем, производная является важным инструментом в математике и ее приложениях.
Как найти производную функции?
Для нахождения производной функции нужно применить правила дифференцирования. Они позволяют вычислить производную для различных типов функций. Например, для постоянной функции, производная всегда равна нулю, а для функции вида f(x) = ax^n, где a и n — константы, производная равна произведению n на a, умноженному на x в степени (n-1).
Что такое производная первого порядка?
Производная первого порядка функции показывает, насколько быстро меняется значение функции при изменении аргумента на единицу. Она определяется как предел отношения изменения функции к изменению аргумента при стремлении изменения аргумента к нулю.
Как можно интерпретировать значение производной?
Значение производной функции в точке можно интерпретировать как скорость изменения функции в данной точке. Если производная положительна, то функция возрастает в этой точке. Если производная отрицательна, то функция убывает. А значение производной равное нулю означает экстремум функции в данной точке.
Производная и определенный интеграл
Производная функции показывает, как изменяется значение функции при изменении ее аргумента. Она является мгновенной скоростью изменения функции в данной точке и обозначается символом f'(x) или dy/dx. Производная позволяет определить наклон касательной к графику функции в данной точке.
Определенный интеграл, с другой стороны, позволяет найти площадь под графиком функции на заданном интервале. Он обозначается символом ∫f(x)dx и является обратным процессом к производной. Если производная показывает скорость изменения функции, то определенный интеграл позволяет найти суммарное изменение функции на заданном интервале.
Связь между производной и определенным интегралом выражается в основной теореме исчисления: если функция f(x) непрерывна на интервале [a, b] и имеет первообразную F(x), то значение определенного интеграла от f(x) на этом интервале равно разности значений первообразной в точках b и a: ∫abf(x)dx = F(b) — F(a).
Использование производной и определенного интеграла позволяет решать различные задачи, связанные с изменением и суммированием функций. Эти два понятия являются основными инструментами дифференциального и интегрального исчисления.

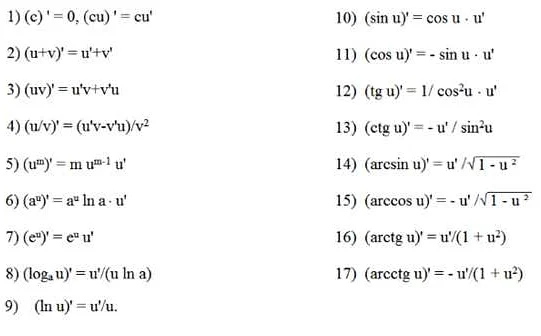


Статья очень хорошо объясняет, что такое производная на простом языке. Я всегда пыталась понять этот концепт, но он казался мне сложным и запутанным. Однако после прочтения этой статьи, я наконец-то поняла, что производная — это просто скорость изменения функции. Пример с автомобилем очень наглядно показывает, как производная может быть использована для измерения скорости изменения. Теперь я понимаю, что если функция меняется быстро, то ее производная будет большой, а если медленно, то маленькой. Это очень полезное понятие, которое можно применить во многих областях, таких как физика и экономика. Статья очень хорошо структурирована и легко читается. Она предоставляет ясные и простые примеры, которые помогают запомнить основные идеи. Я благодарна автору за такое понятное объяснение производной и рекомендую эту статью всем, кто хочет разобраться в этой теме!
Производная — это одно из тех понятий, что многим кажется сложным и непонятным. Но на самом деле, когда начинаешь разбираться, оказывается, что все не так уж и страшно. Производная — это показатель того, как быстро меняется функция в какой-то точке. То есть, она позволяет нам узнать, как функция изменяется, когда мы двигаемся по оси X. Можно представить себе график функции, например, график скорости движения машины. Производная в этом случае покажет, насколько быстро меняется скорость машины в каждый момент времени. Если производная положительная, то скорость растет, а если отрицательная, то скорость уменьшается. Понятие производной очень полезно и применяется во многих областях науки и техники. Например, в физике она помогает определить ускорение тела, а в экономике — рост или спад производства. Но чтобы понять производную, нужно немного времени и упорства. Я сам вначале с трудом разбирался в этой теме, но потом понял, что все дело в понимании основных понятий и правил. Рекомендую начать с поиска хороших учебников и видеоуроков по математике, которые объясняют производную на простом языке. В общем, производная — это не так уж и сложно, как кажется на первый взгляд. Главное — находить подходящий подход к изучению этого понятия и не бояться задавать вопросы. Уверен, что каждый, кто заинтересуется, сможет разобраться в нем и применить это знание на практике.