Дифференцированное уравнение как модель реальных процессов: примеры и решения

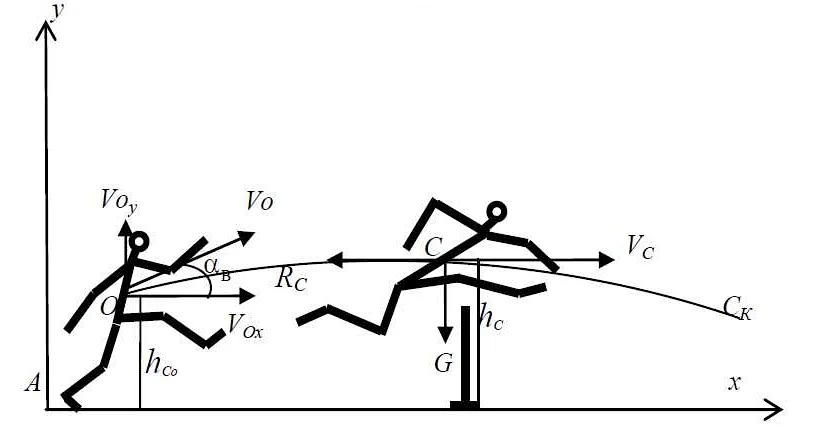
Статья рассказывает об использовании дифференциальных уравнений в качестве математических моделей для описания различных физических, биологических и экономических процессов, таких как распространение эпидемий, движение тел, рост населения и многое другое. Узнайте, как дифференциальные уравнения помогают ученым предсказывать будущее и оптимизировать процессы в различных областях науки и техники.

Дифференцированные уравнения широко используются в математике для моделирования реальных процессов. Они позволяют описывать изменение величин во времени, пространстве и других параметрах. Дифференцированные уравнения широко используются в науке, инженерии и многих других областях для анализа различных процессов и событий.

Дифференцированные уравнения играют ключевую роль в статистической механике, теории поля, теории оптимизации и других областях. Они используются для изучения поведения процессов, связанных с энергией, температурой, скоростью и другими физическими и химическими характеристиками процессов.

Дифференциальные уравнения предоставляют средства для анализа динамических систем, таких как электрические цепи, системы автоматического управления, механические конструкции и многие другие. Дифференцированные уравнения также используются для моделирования экосистем, популяционных динамик и других комплексных систем.

Основы дифференциальных уравнений

Дифференциальные уравнения в математике используются для описания изменения какого-либо процесса во времени. В основе дифференциальных уравнений лежит понятие производной функции. Производная функции показывает скорость изменения значения функции в каждой точке ее определения.

Дифференциальное уравнение представляет собой уравнение, в котором искомой функцией является не сама функция, а ее производная. Решение дифференциального уравнения представляет собой совокупность всех функций, удовлетворяющих уравнению.

Дифференциальные уравнения находят широкое применение в физике, химии, экономике, биологии и других науках, для описания процессов, изменяющихся во времени. Например, закон сохранения энергии в физике может быть выражен в виде дифференциального уравнения, а закон Михайлова-Ментен в биологии используется для описания роста и размножения популяций животных.

• Основные виды дифференциальных уравнений:
  1. Обыкновенные дифференциальные уравнения, которые описывают изменение одной функции относительно независимой переменной.
  2. Частные дифференциальные уравнения, которые описывают изменение нескольких функций относительно нескольких независимых переменных.
• Методы решения дифференциальных уравнений:
  1. Аналитические методы, основанные на выделении и приведении уравнения к стандартному виду.
  2. Численные методы, при которых решение находится численно с помощью компьютерных алгоритмов.

Дифференциальные уравнения позволяют создавать математические модели реальных процессов и предсказывать их поведение в будущем. Они также играют важную роль в науке и различных технических областях.

Видео по теме:

Виды дифференциальных уравнений

Дифференциальное уравнение — это уравнение, которое содержит производные функции. Они широко используются в различных областях науки и инженерии, таких как физика, химия, экономика и биология. Дифференциальные уравнения можно классифицировать по нескольким критериям.

1. По порядку: Порядок дифференциального уравнения определяется самым высоким порядком производной. Примеры: y» + 2y’ + y = x; 2yy’ — x = 0.

2. По виду: Дифференциальные уравнения могут быть линейными, нелинейными, однородными или неоднородными. Линейные уравнения содержат только один член функции или ее производных, нелинейные — несколько членов. Однородные уравнения — это уравнения, в которых все члены зависят от функции или ее производных, неоднородные — уравнения, в которых имеются свободные члены. Примеры: линейное уравнение y» + 2y’ + y = x; неоднородное уравнение y’ — 2y = x^2.

3. По типу переменных: Дифференциальные уравнения могут быть обыкновенными (ОДУ) или частными (ЧДУ). ОДУ содержат только одну переменную, обычно в форме y(x), ЧДУ — уравнения в двух или более переменных, например, y(x, t) или f(x, y, z).

4. По решению: Дифференциальные уравнения могут быть аналитическими (то есть решаемыми с помощью элементарных функций) или численными (вычисляемыми при помощи компьютерных методов, например, методом Эйлера). В некоторых случаях аналитическое решение невозможно (например, для многих нелинейных уравнений).

Классификация дифференциальных уравнений имеет большое значение для их решения и анализа, поэтому важно понимать различия между видами уравнений.

Решение дифференциальных уравнений

Дифференциальные уравнения широко используются для математического моделирования физических, химических и экономических процессов. Решение дифференциальных уравнений позволяет определить зависимость переменных от времени и получить аналитический или численный ответ на вопросы, связанные с прогнозированием переходных процессов, устойчивости системы и оптимизации ее работы.

Существуют различные методы решения дифференциальных уравнений: аналитические, численные и комбинированные. Аналитические методы применяются при наличии точного решения уравнения или его частного случая. Численные методы используются, когда точное решение невозможно или слишком сложно получить. Комбинированные методы предполагают применение как аналитического, так и численного решения для последовательной многократной обработки данных.

Для численного решения дифференциальных уравнений существует множество алгоритмов, таких как методы Эйлера, Рунге-Кутты, Адамса и другие. Однако, выбор метода зависит от типа уравнения и его характеристик. Каждый метод имеет свои преимущества и недостатки, а также порядок точности, который определяет точность расчетов.

Важно учитывать, что решение дифференциального уравнения не всегда является корректным и может давать неверный результат в случае неправильного выбора метода или параметров. Кроме того, при наличии неоднородных условий, решение уравнения может быть получено только в частном виде.

Вопрос-ответ:

Что такое дифференцированное уравнение?

Дифференцированное уравнение — это уравнение, содержащее производные неизвестной функции или нескольких функций от одной или нескольких переменных. Они используются для описания математических моделей реальных процессов различной природы, например, механических, электрических, биологических, экономических и других.

Какая связь между дифференцироваными уравнениями и реальными процессами?

Дифференцированные уравнения позволяют описать динамику различных процессов, которые происходят в реальной жизни. Например, они могут описывать движение тела, изменение температуры, распространение электрического сигнала и т. д. Поэтому они являются одним из важных инструментов при моделировании различных процессов.

В каких областях применяются дифференцированные уравнения?

Дифференцированные уравнения применяются в различных областях науки и техники. Например, они используются при решении задач механики, гидродинамики, электродинамики, оптики, биологии, экономики и др. Кроме того, они широко применяются в моделировании различных процессов в экономике и финансах.

Как решать дифференцированные уравнения?

Решение дифференцированных уравнений — это задача, которую можно решать аналитически или численно. Аналитическое решение выполняется путём нахождения неизвестной функции, которая удовлетворяет заданному уравнению. Численное решение основывается на аппроксимации производных и нахождении значений функции в конечном числе точек с помощью специальных алгоритмов.

Какие методы существуют для решения дифференцированных уравнений?

Существует много методов для решения дифференцированных уравнений. Некоторые из них являются аналитическими и рассчитываются вручную, а другие — численные и выполняются с помощью компьютерных программ. Среди аналитических методов можно назвать методы разделения переменных, метод интегрирующего множителя, метод вариации постоянных и другие. Среди численных методов можно выделить метод Эйлера, метод Рунге-Кутты, метод конечных разностей, метод конечных элементов и другие.

Какие проблемы могут возникнуть при решении дифференцированных уравнений?

При решении дифференцированных уравнений могут возникать различные проблемы. Например, может оказаться сложно или невозможно получить аналитическое решение. Кроме того, при численном решении могут возникнуть ошибки, связанные с неточностью аппроксимации производных и ограниченностью количества точек, в которых вычисляются значения функции. Также может возникнуть проблема выбора наиболее подходящего метода решения уравнения, в зависимости от его характеристик и условий задачи.

Какие применения имеют дифференциальные уравнения в повседневной жизни?

Дифференциальные уравнения имеют много применений в повседневной жизни. Например, они используются при проектировании автомобилей, самолётов, мостов и других конструкций, чтобы определить их жизнеспособность и устойчивость. Они также используются в медицине при моделировании работы сердечно-сосудистой системы и других органов. Кроме того, они находят применение в финансовой математике при анализе поведения цен на фондовом рынке и оценке рисков.

Примеры математических моделей

Модель равновесия цены и количества на рынке

Данная модель является одной из классических задач экономической теории. Она предполагает, что цена и количество товара, которые будут проданы, зависят от спроса и предложения на товар на рынке. Модель может быть представлена в виде уравнения:

Q = f(p)

где Q — количество товара, которое будет продано, а p — цена товара. Функция f описывает зависимость количества продаваемого товара от цены. Данная модель позволяет проводить анализ механизма ценообразования на рынке и принимать решения по формированию цен на товары.

Модель Лотки-Вольтерры

Модель Лотки-Вольтерры используется для описания взаимодействия двух видов в биологической экосистеме. Она предполагает, что количество одного вида животных зависит от количество другого вида животных, на которых он питается. Модель может быть представлена в виде системы дифференциальных уравнений:

• dx/dt = ax — bxy
• dy/dt = dxy — cy

где x и y — количество каждого вида животных, a, b, c, d — константы, описывающие различные параметры жизненного цикла животных. Данная модель позволяет оценить влияние изменения численности одного вида на другой и помогает принимать решения по сохранению биологической разнообразности в экосистеме.

Модель распространения инфекции

Данная модель описывает распространение заболевания среди населения в зависимости от ряда факторов, таких как масштаб контактов между людьми и интенсивность распространения заболевания. Модель может быть представлена в виде системы дифференциальных уравнений:

• S’ = -βSI
• I’ = βSI — γI
• R’ = γI

где S — количество людей, которые могут быть заражены, I — количество инфицированных людей, R — количество людей, которые выздоровели или были иммунизированы, β — коэффициент заражения, γ — коэффициент выздоровления. Данная модель позволяет оценить эффективность различных мер для борьбы с распространением инфекции и оценить возможность контроля заболевания.

Приложения дифференциальных уравнений в физике

Дифференциальные уравнения имеют огромное значение в физике и используются для описания законов движения материи и энергии в природе. Некоторые из наиболее известных и важных приложений дифференциальных уравнений в физике включают в себя следующее:

• Закон Ньютона: Для описания движения твердого тела используют уравнение Ньютона, которое связывает силу, массу и ускорение объекта. Это уравнение является дифференциальным и может быть написано в форме второго порядка.
• Закон сохранения энергии: Дифференциальные уравнения используются для описания закона сохранения энергии. Этот закон утверждает, что энергия не создается и не уничтожается, а только преобразуется из одной формы в другую. Он может быть записан в форме дифференциального уравнения в частных производных.
• Закон Гука: Закон Гука, который описывает связь между силой, деформацией и упругим модулем, также может быть записан в форме дифференциального уравнения. Этот закон важен для описания поведения материалов при деформации и может быть использован для описания напряжения и деформации тел.
• Уравнение теплопроводности: Дифференциальное уравнение теплопроводности используется для описания распространения тепла в твердых телах. Оно является одним из основных уравнений термодинамики и может быть использовано для моделирования различных процессов, таких как охлаждение материала или теплопередача через стенку.
• Уравнение Навье-Стокса: Уравнение Навье-Стокса является основным уравнением теории жидкости и газа и используется для описания движения жидкостей и газов. Это уравнение является дифференциальным и может быть использовано для моделирования течения жидкостей через трубы и каналы, а также для прогнозирования погоды и климатических условий.

В целом, дифференциальные уравнения являются очень мощным инструментом в физике и позволяют нам создавать математические модели для описания и предсказания поведения систем в природе.

Приложения дифференциальных уравнений в экономике

Дифференциальные уравнения применяются в экономике для решения множества задач, связанных с моделированием экономических процессов. В общем случае, экономические модели с помощью дифференциальных уравнений описывают динамику изменения социальных и экономических показателей во времени.

Например, дифференциальные уравнения используются для описания роста населения в отдельных регионах и странах, а также для определения уровня безработицы. Также с помощью дифференциальных уравнений строятся модели, описывающие развитие финансовых рынков, таких как рынки ценных бумаг и валютных пар.

Одной из важнейших областей экономики, где применяются дифференциальные уравнения, является теория экономического роста. Многие модели экономического роста обязаны своим развитием именно дифференциальным уравнениям.

Еще одним примером применения дифференциальных уравнений в экономике является моделирование закономерностей связанных с потребительским поведением. Например, с помощью дифференциальных уравнений можно описать развитие рынков товаров и услуг, понимание технического прогресса и повышение планирования объемов производства.

Таким образом, дифференциальные уравнения являются незаменимым инструментом в экономике для создания компьютерных моделей и прогнозирования экономических процессов. Применение данного математического метода помогает сократить время получения и анализа данных, а также сократить вероятность возникновения ошибок при принятии решений.

Приложения дифференциальных уравнений в биологии

Дифференциальные уравнения широко применяются в биологии для моделирования различных процессов, таких как рост, размножение, распространение болезней, изменения популяции и многое другое. Простые математические модели, основанные на дифференциальных уравнениях, позволяют описать сложные биологические процессы и выявить закономерности, которые не всегда видны на поверхности.

Одним из наиболее известных примеров применения дифференциальных уравнений в биологии является уравнение модели роста популяции.

Уравнение модели роста популяции: dN/dt = rN(K-N)/K

Здесь N — количество особей в популяции, t — время, r — скорость роста популяции, K — емкость среды. Это уравнение позволяет определить, какие факторы ограничивают рост популяции и как эти факторы будут влиять на размер популяции в будущем.

Еще одна область применения дифференциальных уравнений в биологии — это моделирование распространения болезней. Уравнения моделирования распространения болезней помогают выявлять факторы, которые влияют на скорость и масштаб распространения болезней, а также описывают траекторию эпидемии.

Таким образом, использование дифференциальных уравнений в биологии помогает получить более глубокое понимание различных процессов, происходящих в живых системах, и помогает улучшить прогнозирование их дальнейшего развития.

Приложения дифференциальных уравнений в технике

Дифференциальные уравнения находят широкое применение в технике и инженерии. Они позволяют описывать многие процессы, которые встречаются в реальном мире, и предсказывать поведение систем в различных условиях.

Например, дифференциальные уравнения используются для моделирования движения объектов в пространстве. Они могут помочь определить путь и скорость движения, а также предсказать будущее положение объекта.

Дифференциальные уравнения также используются в электротехнике для расчета электрических цепей. Они могут помочь определить ток и напряжение в различных точках цепи, а также предсказать поведение системы при изменении параметров.

В механике дифференциальные уравнения применяются для моделирования динамики систем. Они могут помочь определить силы, действующие на объекты, а также предсказать их движение в различных условиях.

Также дифференциальные уравнения используются в химии, биологии, экономике, и других областях науки и техники. Их применение позволяет улучшать процессы и системы, разрабатывать новые технологии и предсказывать поведение объектов и систем в различных условиях.

Преимущества и недостатки механических и численных методов решения

Механические методы

Основным преимуществом механических методов решения дифференциальных уравнений является их универсальность. Они могут использоваться для решения самых разных задач, не зависят от типа дифференциального уравнения и могут обрабатывать сложные нелинейные функции. Это позволяет решить многие задачи, которые не могут быть решены любыми другими методами.

Однако у механических методов есть и недостатки. Они могут быть очень грубыми приближениями и не гарантируют точности результата. Кроме того, процесс решения обычно рабочий и ручной, что требует много времени и умения. Это может стать проблемой при решении больших и сложных задач и может снизить эффективность и точность результата.

Численные методы

Одним из основных преимуществ численных методов является быстрота вычислений и автоматический характер процесса решения. Это дает возможность решать очень сложные и большие задачи, которые невозможно решить другими методами. Кроме того, точность результата может быть контролируемой, и если нужно, ее можно увеличить путем улучшения способа аппроксимации уравнения.

С другой стороны, численные методы могут стать нежелательными опциями в случаях, когда требуется высокая точность результата. Неизбежная аппроксимация уравнения может привести к потере точности, а также обратимость численной процедуры может быть неопределенной. Кроме того, эти методы могут быть неприменимыми в случае, когда уравнение содержит специальные условия или ограничения на решение.