Что такое дифференцирование в математике простыми словами

Дифференцирование в математике – это процесс нахождения производной функции, который позволяет определить скорость изменения функции в каждой точке графика. В данной статье мы рассмотрим основные принципы дифференцирования и объясним их простыми словами.

Дифференцирование – это важное понятие в математике, которое позволяет нам изучать изменения функций. Оно используется для нахождения скорости изменения функции в каждой ее точке и помогает понять, как функция меняется при изменении ее аргумента. Дифференцирование является основой дифференциального исчисления и имеет широкое применение в различных областях науки и техники.

Основное понятие, связанное с дифференцированием, — это производная функции. Производная функции в точке показывает, как быстро функция меняется в этой точке. Она определяется как предел отношения приращения функции к приращению аргумента при стремлении приращения аргумента к нулю. Производная функции может быть положительной, отрицательной или нулевой в зависимости от того, растет, убывает или остается постоянной функция в данной точке.

Дифференцирование основывается на нескольких основных правилах, которые позволяют нам находить производные функций различных типов. Одно из таких правил — правило дифференцирования суммы, которое гласит, что производная суммы двух функций равна сумме производных этих функций. Еще одно важное правило — правило дифференцирования произведения, которое утверждает, что производная произведения двух функций равна произведению производной первой функции на вторую функцию плюс произведение первой функции на производную второй функции.

Основы дифференцирования

Производная функции показывает, как изменяется значение функции при изменении ее аргумента. Она определяется как предел отношения изменения функции к изменению аргумента при стремлении изменения аргумента к нулю. Производная функции в точке может быть как положительной, так и отрицательной, а также может быть равной нулю.

Дифференцирование позволяет нам решать различные задачи, такие как нахождение экстремумов функции, определение скорости изменения функции в определенной точке, определение формы графика функции и многое другое.

Для нахождения производной функции, существуют различные правила дифференцирования, такие как правило суммы, правило произведения, правило частного и т.д. С их помощью можно вычислить производную сложной функции, комбинировать различные функции и находить их производные.

Дифференцирование находит свое применение во многих областях, таких как физика, экономика, биология и даже компьютерные науки. Оно помогает нам понять и описать различные явления и процессы, а также решать различные задачи в этих областях.

Изучение основ дифференцирования является важным шагом в обучении математике и позволяет нам глубже понять и использовать различные математические концепции и методы для анализа функций и их поведения.

Что такое дифференцирование?

Дифференцирование является одной из основных операций в математическом анализе и используется во многих областях, таких как физика, экономика, инженерия и другие. Оно позволяет изучать поведение функций, оптимизировать процессы и решать различные задачи.

Дифференцирование производится с помощью математического оператора, называемого производной. Производная функции обозначается как f'(x) или dy/dx. Она показывает, как изменяется значение функции в зависимости от изменения аргумента.

Для того чтобы найти производную функции, необходимо применить определенные правила дифференцирования. Они позволяют найти производную для различных типов функций, таких как полиномы, экспоненциальные и тригонометрические функции.

Дифференцирование имеет много свойств и приложений. С его помощью можно находить экстремумы функций, исследовать форму графиков, находить скорость изменения величин и многое другое.

Дифференцирование играет важную роль в математике и науке, и является одной из основных операций для изучения функций и их свойств.

Зачем нужно дифференцирование?

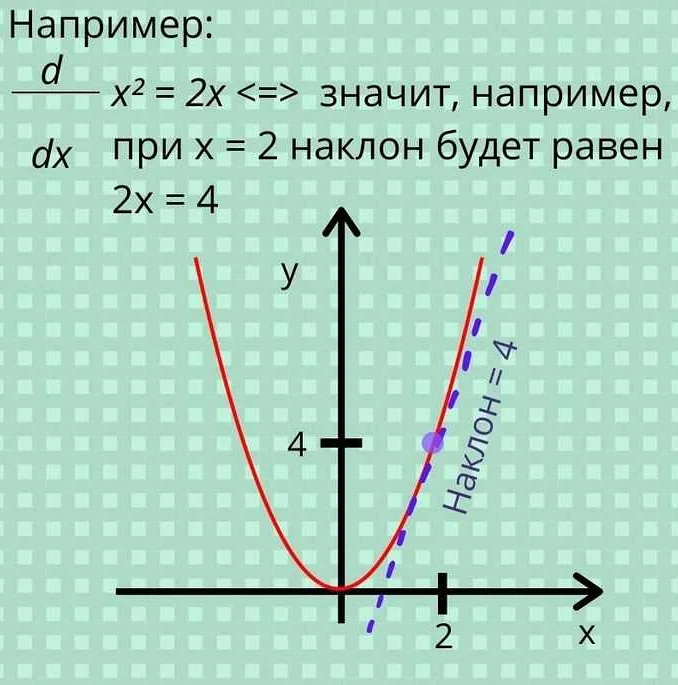
Основная задача дифференцирования — найти производную функции. Производная функции в каждой точке показывает наклон касательной к этой функции в данной точке. Это позволяет нам понять, как функция меняется по мере изменения аргумента.

Дифференцирование имеет широкое применение в различных областях, таких как физика, экономика, биология и технические науки. Например, в физике производная функции расстояния по времени показывает скорость движения тела, а в экономике производная функции спроса показывает эластичность спроса на товары.

Область примененияПримеры

Физика	Скорость, ускорение, сила
Экономика	Спрос, предложение, доходность
Биология	Рост популяции, мутации
Технические науки	Теплопроводность, электрические силы

В заключение, дифференцирование является мощным инструментом для анализа и понимания функций, и находит широкое применение в науке и практике. Оно позволяет нам определить скорость изменения функции и ее градиент, а также найти точки экстремума. Дифференцирование является неотъемлемой частью математики и имеет множество применений в реальном мире.

Простое объяснение дифференцирования

Производная функции в точке определяется как предел отношения приращения значения функции к приращению ее аргумента при стремлении приращения аргумента к нулю.

Для понимания дифференцирования полезно вспомнить, что производная функции показывает наклон касательной к ее графику в каждой точке. Если производная положительна, то график функции в данной точке возрастает; если производная отрицательна, то график функции убывает. Если производная равна нулю, то график функции имеет экстремум (максимум или минимум) в этой точке.

Таким образом, дифференцирование позволяет нам анализировать поведение функции и находить экстремумы, касательные и другие важные характеристики ее графика.

Математические понятия в дифференцировании

Производная функции показывает, как меняется значение функции при изменении ее аргумента. Она определяется как предел отношения приращения функции к приращению ее аргумента, когда приращение аргумента стремится к нулю.

Дифференцирование в математике основано на нескольких ключевых понятиях:

• Предел функции: представляет собой значение, к которому стремится функция приближаясь к определенной точке или значениям аргумента.
• Функция: определяет зависимость одной величины от другой. В контексте дифференцирования, функция обычно обозначается как y = f(x), где y — значение функции, а x — аргумент.
• Границы и интервалы: для дифференцирования важно определить область определения функции, а также интервалы, на которых будет проводиться операция дифференцирования.
• Приращение функции и аргумента: для вычисления производной необходимо знать изменение значения функции и изменение значения аргумента.
• Производная функции: является основным результатом дифференцирования и показывает скорость изменения функции в каждой точке. Она обозначается как f'(x) или df/dx.

Понимание этих математических понятий в дифференцировании позволяет более точно анализировать и изучать функции, их свойства и поведение.

Производная функции: определение и свойства

Определение производной функции заключается в нахождении предела отношения изменения функции к изменению ее аргумента при стремлении этого изменения к нулю. Формально производная функции f(x) в точке x0 определяется следующим образом:

где h — бесконечно малое число, представляющее изменение аргумента функции, и f(x0) — значение функции в точке x0.

Производная функции имеет несколько свойств, которые позволяют упростить ее вычисление и анализ:

СвойствоФормула

Линейность	(f + g)′(x) = f′(x) + g′(x)
Правило произведения	(f * g)′(x) = f′(x) * g(x) + f(x) * g′(x)
Правило частного	(f/g)′(x) = (f′(x) * g(x) — f(x) * g′(x)) / (g(x))^2
Правило цепочки	(f(g(x)))′ = f′(g(x)) * g′(x)

Эти свойства позволяют проводить дифференцирование сложных функций и выражений. Знание производной функции и ее свойств является важным инструментом в исследовании и оптимизации функций, а также в решении задач из различных областей науки и инженерии.

Как найти производную?

Существуют различные способы нахождения производной функции, в зависимости от вида функции и задачи, которую нужно решить.

• Производная от константы: Если функция f(x) является константой (не зависит от x), то ее производная равна нулю.
• Производная от степенной функции: Если функция f(x) = x^n, где n — целое число, то ее производная равна произведению степени и коэффициента: f'(x) = nx^(n-1).
• Производная от суммы функций: Если функция f(x) = g(x) + h(x), где g(x) и h(x) — две функции, то производная от суммы функций равна сумме производных: f'(x) = g'(x) + h'(x).

Это лишь некоторые примеры, как найти производную функции. В общем случае, для нахождения производной функции, необходимо использовать правила дифференцирования и знать основные формулы. Существуют также таблицы производных, которые содержат информацию о производных для различных функций.

Дифференцирование имеет широкое применение в различных областях науки и инженерии. Оно позволяет находить скорость изменения величин, оптимизировать процессы и моделировать сложные системы.

Вопрос-ответ:

Как можно объяснить дифференцирование в математике?

Дифференцирование — это процесс нахождения производной функции. Производная функции показывает, как быстро меняется значение функции в каждой точке. Можно представить это как измерение скорости изменения — производная функции показывает, насколько быстро значение функции меняется при изменении ее аргумента.

Каким образом производная функции помогает в решении задач?

Производная функции является одним из наиболее важных понятий в математике и широко используется во многих областях. Она позволяет найти касательные и нормали к графику функции, определить экстремумы функции, анализировать рост или убывание функции, находить точки перегиба и многое другое. Производная также позволяет решать задачи оптимизации и находить максимумы и минимумы функций.

Как найти производную функции?

Для нахождения производной функции нужно применить определенные правила дифференцирования. Существуют базовые правила дифференцирования, такие как правило суммы, правило произведения, правило деления и правило цепной дифференциации. Используя эти правила, можно находить производные сложных функций и функций, состоящих из нескольких частей. В некоторых случаях, для нахождения производных, требуется использовать специальные методы, например, правило Лейбница или правило Лопиталя.

Как определить экстремумы функции с помощью производной?

Экстремумы функции можно определить, исследуя ее производную. Если производная функции равна нулю в некоторой точке, то это может быть признаком экстремума. Если производная меняет знак с плюса на минус в некоторой точке, то это может быть признаком локального максимума, а если с минуса на плюс — признаком локального минимума. Для определения глобального экстремума требуется дополнительное исследование функции на бесконечностях и на концах промежутка.

Какое значение имеет дифференцирование в математике?

Дифференцирование в математике является одной из основных операций математического анализа. Оно позволяет находить производные функций, что является ключевым инструментом в изучении и анализе функций и их свойств. Дифференцирование также позволяет определить скорость изменения функции в данной точке, а также найти касательные и нормали к графику функции.

Примеры применения дифференцирования

1. Определение экстремумов: Дифференцирование позволяет найти точки, где функция достигает локального минимума или максимума. Это особенно полезно в оптимизации, экономике, физике и других дисциплинах, где необходимо найти наилучшие результаты.
2. Нахождение скорости и ускорения: Дифференцирование позволяет вычислить скорость и ускорение объекта в зависимости от времени. Это очень полезно в физике и инженерии, где необходимо изучать движение объектов и оценивать их характеристики.
3. Исследование графиков функций: Дифференцирование позволяет анализировать графики функций и определять их поведение в различных точках. Например, дифференцирование может помочь определить, где функция возрастает или убывает, а также найти точки перегиба.
4. Решение уравнений: Дифференцирование может быть использовано для решения различных математических и физических задач. Например, дифференциальные уравнения, которые включают производные, могут быть решены путем дифференцирования.
5. Аппроксимация и анализ данных: Дифференцирование может быть использовано для аппроксимации и анализа экспериментальных данных. Например, производная функции может помочь определить момент времени, когда зависимость между переменными наиболее сильна.

Это только несколько примеров, как дифференцирование может быть применено в различных областях. Понимание основных понятий дифференцирования может помочь в решении различных задач и улучшить понимание математических моделей и явлений.

Видео по теме: