Что такое длина в математике
Содержимое
- 1 Что такое длина в математике
- 1.1 Что такое длина в математике: объяснение и примеры
- 1.2 Определение понятия длины в математике
- 1.3 Единицы измерения длины
- 1.4 Как измерить длину отрезка
- 1.5 Сравнение длин: как определить, какой отрезок длиннее
- 1.6 Длина линии: примеры и объяснение
- 1.7 Длина окружности и путь: отличия и примеры
- 1.8 Длина фигуры: как определить длину прямоугольника, треугольника и других фигур
- 1.9 Название сайта
- 1.10 Вопрос-ответ:
- 1.10.0.1 Что такое длина в математике?
- 1.10.0.2 Как измерить длину отрезка?
- 1.10.0.3 Какая единица измерения используется для измерения длины в математике?
- 1.10.0.4 Какие могут быть примеры измерения длины в математике?
- 1.10.0.5 Какая связь между длиной и периметром?
- 1.10.0.6 Что такое длина в математике?
- 1.10.0.7 Как можно измерить длину?
- 1.11 Видео по теме:
Длина в математике является мерой измерения протяженности объекта или расстояния между двумя точками. Узнайте, как определить и измерить длину в различных областях математики и ее значимость в решении задач и проблем.
Длина является одним из фундаментальных понятий в математике. Она измеряет расстояние между двумя точками или объектами. В математике используется несколько способов определения длины, в зависимости от типа объекта, который нужно измерить.
Для измерения длины прямой линии используется понятие абсолютной длины. Абсолютная длина является физической величиной и измеряется в метрах, сантиметрах или других единицах измерения длины. Например, чтобы измерить длину стола, можно использовать линейку или мерную ленту.
Однако в математике также используется понятие относительной длины. Относительная длина не связана с физической величиной, а является абстрактным понятием. Она измеряется с помощью чисел или других математических объектов. Например, в геометрии длина отрезка может быть представлена числом или выражением.
Длина является важным понятием во многих областях математики, таких как геометрия, алгебра, теория вероятностей и другие. Понимание длины позволяет решать различные математические задачи и строить точные модели реальных явлений.
В данной статье мы рассмотрим основные понятия и примеры использования длины в математике. Мы рассмотрим различные способы измерения длины и обсудим их применение в разных математических областях. Понимание длины поможет вам лучше понять и применять математические концепции в вашей повседневной жизни и в решении различных задач.
Что такое длина в математике: объяснение и примеры
Одной из самых простых и понятных формул, которая используется для вычисления длины, является формула длины отрезка:
ФормулаОписание
| AB = √((x2 — x1)2 + (y2 — y1)2) | Формула длины отрезка AB, где (x1, y1) и (x2, y2) — координаты точек A и B соответственно |
Пример: Для отрезка AB с координатами A(1, 2) и B(4, 6) вычислим его длину:
AB = √((4 — 1)2 + (6 — 2)2)
AB = √(32 + 42)
AB = √(9 + 16)
AB = √25
AB = 5
Таким образом, длина отрезка AB равна 5 единицам.
Помимо длины отрезка, в математике также используются другие понятия длины, такие как длина окружности, длина дуги и т.д. В каждом случае формула для вычисления длины будет своей и зависеть от конкретной геометрической формы.
Определение понятия длины в математике

Длина может быть измерена в различных единицах, таких как метры, сантиметры, футы и т. д. Для измерения длины используют специальные инструменты, такие как линейка или мерная лента.
В математике длина может быть представлена числовым значением или символом, обозначающим эту величину. Например, длину отрезка AB можно обозначить как «AB» или «l», где l — это численное значение длины.
Длина имеет ряд свойств, которые используются при решении математических задач. Например, длина отрезка всегда положительна и не может быть отрицательной числом. Кроме того, длина отрезка не изменяется при его параллельном переносе или вращении.
Определение понятия длины является основой для изучения других величин и свойств в математике, таких как площадь, объем и т. д. Понимание длины позволяет решать различные задачи, связанные с измерением и оценкой расстояний в пространстве.
Единицы измерения длины
В математике существует несколько единиц измерения длины, которые используются для измерения размеров объектов и расстояний между ними. Наиболее распространенные единицы измерения длины включают:
Метр (м) — основная единица измерения длины в Международной системе единиц (СИ). Метр определяется как расстояние, которое свет проходит в вакууме за время 1/299 792 458 секунды.
Километр (км) — равен 1000 метрам или 10^3 метрам.
Сантиметр (см) — равен одной сотой части метра или 0.01 метра.
Миллиметр (мм) — равен одной тысячной части метра или 0.001 метра.
Микрометр (мкм) — равен одной миллионной части метра или 0.000001 метра.
Нанометр (нм) — равен одной миллиардной части метра или 0.000000001 метра.
Ангстрем (Å) — равен 0.0000000001 метра или 0.1 нанометра.
Ярд (yd) — единица измерения длины, широко используемая в Соединенных Штатах и Великобритании. Один ярд равен примерно 0.9144 метра.
Фут (ft) — единица измерения длины, также используемая в Соединенных Штатах и Великобритании. Один фут равен примерно 0.3048 метра.
Дюйм (in) — единица измерения длины, также используемая в Соединенных Штатах и Великобритании. Один дюйм равен примерно 0.0254 метра.
Морская миля (миля) — единица измерения длины, используемая в морской навигации и авиации. Одна морская миля равна примерно 1852 метрам.
Это лишь некоторые из множества единиц измерения длины, которые применяются в математике и в повседневной жизни. Выбор конкретной единицы измерения длины зависит от контекста и требований задачи.
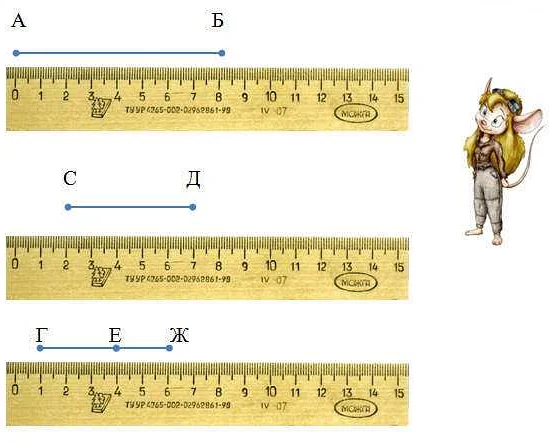
Как измерить длину отрезка

Для измерения длины отрезка в математике можно использовать различные методы и инструменты.
Один из самых простых способов — использование линейки или мерной ленты. При помощи этого инструмента можно измерить длину отрезка, размещая его на линейке и считывая соответствующие значения.
Если отрезок имеет нестандартную форму или не может быть полностью помещен на линейку, можно использовать другие методы. Например, можно разделить отрезок на несколько частей, измерить их длины, а затем сложить полученные значения.
Также существуют специальные устройства, например, лазерные измерители расстояний, которые позволяют измерить длину отрезка с высокой точностью.
Независимо от выбранного метода, для получения точного результата необходимо аккуратно проводить измерения, избегая смещений и искажений.
Сравнение длин: как определить, какой отрезок длиннее
Для определения, какой отрезок длиннее, нужно сравнить их длины. Длина отрезка обозначается числом и измеряется в соответствующих единицах измерения, например, метрах или сантиметрах.
Сравнение длин производится с помощью математического оператора «больше» (>), который позволяет определить, какое из двух чисел больше. Если длина первого отрезка больше длины второго отрезка, то можно сказать, что первый отрезок длиннее. Если же длина второго отрезка больше длины первого отрезка, то второй отрезок будет длиннее.
Например, если первый отрезок имеет длину 5 сантиметров, а второй отрезок — 3 сантиметра, то можно сказать, что первый отрезок длиннее второго. Это можно записать так: 5 сантиметров > 3 сантиметра.
Таким образом, для сравнения длин отрезков необходимо знать их длины и использовать оператор «больше» для определения, какой отрезок длиннее.
Длина линии: примеры и объяснение
В математике длина линии определяется как расстояние между двумя точками на этой линии. Расстояние измеряется в единицах длины, таких как сантиметры, метры или футы.
Рассмотрим несколько примеров, чтобы лучше понять, как находить длину линии. Представим, что у нас есть прямая линия, соединяющая точки A и B. Чтобы найти длину этой линии, мы можем использовать теорему Пифагора.
Точка AТочка BДлина линии
| 0 | 3 | 3 |
| 2 | 6 | 4 |
| 5 | 12 | 13 |
В первом примере, если точка A имеет координату 0, а точка B имеет координату 3, то длина линии будет равна 3. Во втором примере, если точка A имеет координату 2, а точка B имеет координату 6, то длина линии будет равна 4. В третьем примере, если точка A имеет координату 5, а точка B имеет координату 12, то длина линии будет равна 13.
Это всего лишь несколько примеров, но их достаточно, чтобы понять, что длина линии зависит от расстояния между двумя точками на этой линии. Нахождение длины линии является важным концептом в математике и широко применяется в различных областях, таких как геометрия, физика и инженерия.
Длина окружности и путь: отличия и примеры
Путь — это длина пути, пройденного объектом при перемещении из одной точки в другую. Путь может быть нелинейным и не обязательно ограничен окружностью. Длина пути вычисляется как сумма расстояний между последовательными точками на пути.
Отличие между длиной окружности и путем заключается в том, что длина окружности является характеристикой замкнутой кривой, в то время как путь измеряет длину пройденного пути между двумя точками. Длина окружности всегда будет зависеть от радиуса окружности, в то время как путь может быть произвольным.
Рассмотрим пример: пусть у нас есть окружность с радиусом 5 см. Длина окружности будет равна 2π * 5 = 10π см. Если объект двигается по окружности один раз, то его путь будет равен длине окружности — 10π см. Однако, если объект движется только частично по окружности, то его путь будет меньше длины окружности.
Длина фигуры: как определить длину прямоугольника, треугольника и других фигур
Для прямоугольника длина определяется по формуле: длина = 2 * (ширина + высота). Например, если прямоугольник имеет ширину 5 см и высоту 3 см, то его длина будет равна 2 * (5 + 3) = 16 см.
Для треугольника длина определяется суммой длин всех его сторон. Например, если треугольник имеет стороны длиной 4 см, 5 см и 6 см, то его длина будет равна 4 + 5 + 6 = 15 см.
Для других фигур, таких как окружность или эллипс, длина определяется по специальным формулам, связанным с их радиусами или полуосями.
Расчет длины фигуры является важным шагом при решении задач по геометрии и в других областях математики. Знание формул и методов расчета длины позволяет нам более точно анализировать и понимать свойства и характеристики различных фигур.
Название сайта
На нашем сайте «Название сайта» вы найдете множество полезных материалов на различные темы, связанные с математикой. Мы стремимся предоставить всю необходимую информацию и объяснения в понятной и доступной форме.
Наши статьи содержат объяснения основных математических концепций и понятий, а также примеры и задачи, помогающие закрепить полученные знания. Мы также предлагаем шаг за шагом инструкции и подробные решения для различных типов задач.
Наш сайт подходит как для начинающих, так и для продвинутых студентов. Мы стараемся подойти к каждому уровню знаний и предложить материалы, которые будут полезны и интересны для всех.
Мы постоянно обновляем информацию на сайте, добавляя новые статьи, задачи и объяснения. Вы всегда найдете новые и актуальные материалы на нашем сайте. Мы также открыты к предложениям и идеям от наших посетителей, и всегда готовы обсудить новые темы и материалы для размещения на сайте.
Мы надеемся, что наш сайт поможет вам расширить свои знания в математике и сделает изучение этого предмета более интересным и увлекательным.
Вопрос-ответ:
Что такое длина в математике?
В математике длина — это измерение отрезка или расстояния между двумя точками. Она определяется как количество единичных отрезков, которые помещаются в данном отрезке.
Как измерить длину отрезка?
Для измерения длины отрезка можно использовать линейку или мерную ленту. Необходимо разместить начало отрезка в нулевой точке шкалы и определить количество единиц измерения, которые соответствуют данному отрезку.
Какая единица измерения используется для измерения длины в математике?
В математике часто используется единица измерения — метр. Однако, в зависимости от конкретной задачи или контекста, могут использоваться и другие единицы измерения, такие как сантиметры, дециметры, километры и т.д.
Какие могут быть примеры измерения длины в математике?
Примерами измерения длины могут быть: длина стороны квадрата, длина отрезка на оси координат, длина окружности, длина прямой линии между двумя точками и т.д.
Какая связь между длиной и периметром?
Периметр — это сумма длин всех сторон фигуры. Таким образом, длины сторон влияют на периметр фигуры. Например, для квадрата длина каждой стороны равна, а периметр равен умножению длины стороны на 4.
Что такое длина в математике?
В математике длина — это мера расстояния между двумя точками. Она измеряется в единицах длины, таких как метры, сантиметры, футы и т. д. Длина может быть измерена на прямой линии или по кривой.
Как можно измерить длину?
Длину можно измерить с помощью линейки, мерной ленты или другого измерительного инструмента. Для измерения длины на прямой линии достаточно поставить начало измерения в одной точке и переместить его к другой точке, считая количество единиц длины на инструменте. Если нужно измерить длину по кривой, можно использовать изгибаемый инструмент или аппроксимировать кривую прямыми отрезками и измерить их длины.


Длина в математике — это одна из основных характеристик геометрических фигур. Она определяет, насколько длинная или короткая фигура или отрезок. Важно понимать, что длина не зависит от ориентации фигуры в пространстве, она определяется только ее размером. Длина может быть выражена в различных единицах измерения, таких как метры, сантиметры, дюймы и тому подобное. Например, если у нас есть отрезок длиной 5 метров, это означает, что он равен 500 сантиметрам или 196,85 дюймам. Чтобы наглядно представить себе длину, представьте линейку. Она помогает измерять длину различных объектов. Например, вы можете измерить длину стола или шкафа, используя линейку. Если вы знаете, что стол имеет длину 1 метр, то вы можете легко сравнить его с другими объектами. Длина также важна в геометрии, где она используется для нахождения периметра фигур. Периметр — это сумма длин всех сторон фигуры. Например, если у нас есть квадрат со стороной 4 см, то его периметр будет равен 16 см (4+4+4+4). Таким образом, длина в математике является фундаментальным понятием и играет важную роль в различных областях науки. Она помогает измерять и сравнивать объекты, а также использовать их для выполнения различных математических расчетов.
В математике понятие длины является одним из основных и важных. Длина — это мера расстояния между двумя точками на прямой или на поверхности. Это понятие используется в различных областях математики, физики, геометрии и даже в повседневной жизни. Рассмотрим примеры для более наглядного объяснения. Возьмем прямую линию и выберем две ее точки. Для определения длины отрезка между этими точками мы можем использовать линейку или мерную ленту. Например, если длина этого отрезка равна 5 сантиметрам, мы можем сказать, что его длина равна 5 см. Длина также может быть измерена на плоскости, например, при измерении длины сторон прямоугольника или треугольника. В этом случае, мы также можем использовать линейку или измерительную ленту. Например, если мы измерим сторону треугольника и получим значение 10 сантиметров, то мы можем сказать, что длина этой стороны равна 10 см. Однако длина может быть измерена и на более сложных фигурах, таких как окружность или кривая. В этом случае, мы не можем использовать прямую линейку, и для измерения длины используются специальные формулы или методы, такие как интегралы. Таким образом, длина в математике является важным понятием и используется для измерения расстояний между точками или объектами на прямой, плоскости или в пространстве. Понимание этого понятия поможет нам более точно и акуратно работать с геометрическими фигурами и решать различные задачи.
Статья очень понятно объясняет, что такое длина в математике. Я всегда интересовался этой темой, но не всегда мог найти понятные объяснения. В статье дается простое определение длины — это мера расстояния между двумя точками. Это позволяет нам измерять и сравнивать объекты в пространстве. Мне понравилось, что в статье приведены несколько примеров, которые помогают усвоить материал. Например, они объясняют, как измерить длину отрезка на числовой оси или как найти длину окружности. Это помогает лучше понять, как применять понятие длины на практике. Также статья рассматривает единицы измерения длины и объясняет, как переводить их друг в друга. Это полезная информация, которая поможет мне в повседневной жизни, например, при выборе правильного размера одежды или измерении расстояний на карте. Я действительно оценил эту статью и узнал много нового о длине в математике. Теперь я чувствую себя увереннее, когда речь заходит о измерении и сравнении объектов. Большое спасибо автору за ясное объяснение и примеры!