Что такое дополнительные углы в математике
Содержимое
- 1 Что такое дополнительные углы в математике
- 1.1 Определение дополнительных углов
- 1.2 Видео по теме:
- 1.3 Примеры дополнительных углов
- 1.4 Свойства дополнительных углов
- 1.5 Вопрос-ответ:
- 1.6 Как находить дополнительные углы
- 1.7 Значение дополнительных углов в геометрии
- 1.8 Применение дополнительных углов в реальной жизни
- 1.9 Закономерности и особенности дополнительных углов
Дополнительные углы в математике — это пара углов, сумма которых равна 180 градусов. Узнайте, как определить дополнительные углы и как они используются в геометрии и тригонометрии.
В математике существуют различные виды углов, которые играют важную роль при решении геометрических задач. Одним из таких видов являются дополнительные углы. Дополнительные углы — это два угла, сумма которых равна 180 градусам.
Определение дополнительных углов можно выразить следующей формулой: α + β = 180°, где α и β — это дополнительные углы. Таким образом, если известно значение одного угла, можно легко найти значение другого, при условии, что они являются дополнительными.
Пример: Пусть у нас есть два угла: α = 45°. Тогда находим значение второго угла, используя формулу для дополнительных углов: β = 180° — α = 180° — 45° = 135°. Таким образом, если один угол равен 45°, то другой угол будет равен 135°.
Дополнительные углы широко используются в геометрии для решения различных задач. Например, они могут быть использованы для вычисления неизвестных углов в треугольниках, прямоугольниках или параллелограммах. Знание определения и свойств дополнительных углов поможет вам легко и быстро решать подобные задачи, а также углубить понимание геометрических принципов.
Определение дополнительных углов
Дополнительные углы могут быть расположены как внутри, так и снаружи параллельных линий, а также могут быть образованы пересекающимися линиями.
Например, если имеется два угла: один угол равен 60 градусов, то второй угол будет равен 180 — 60 = 120 градусов. В таком случае, эти два угла являются дополнительными.
Дополнительные углы играют важную роль в геометрии и широко используются в решении задач на построение и вычисление углов.
Видео по теме:
Примеры дополнительных углов
Пример 1:
Пусть дан угол A, измеряемый 60 градусами. Тогда его дополнительный угол B будет равен 180 — 60 = 120 градусам.
Пример 2:
Если угол C измеряет 90 градусов, то его дополнительный угол D будет равен 180 — 90 = 90 градусов.
Пример 3:
Дополнительные углы также могут быть отрицательными. Например, если угол E измеряет 200 градусов, то его дополнительный угол F будет равен 180 — 200 = -20 градусов.
Примечание: Дополнительные углы могут быть как внутренними (соседними), так и внешними (противолежащими). В обоих случаях их сумма будет равна 180 градусам.
Свойства дополнительных углов
Свойство 1: Если два угла являются дополнительными, то каждый из них является дополнением другого. То есть, если угол A и угол B являются дополнительными, то угол A также является дополнением угла B, и наоборот.
Свойство 2: Если угол A и угол B являются дополнительными, а угол B и угол C являются дополнительными, то угол A и угол C также являются дополнительными.
Свойство 3: Если два угла являются дополнительными, то каждый из них является остроугольным или тупоугольным. То есть, если сумма двух углов равна 180 градусов, то каждый из этих углов может быть остроугольным (меньше 90 градусов) или тупоугольным (больше 90 градусов).
Использование этих свойств позволяет решать задачи на нахождение неизвестных углов, если известны значения дополнительных углов.
Вопрос-ответ:
Что такое дополнительные углы в математике?
Дополнительные углы — это пара углов, сумма которых равна 180 градусам.
Как определить, что углы являются дополнительными?
Углы являются дополнительными, если их сумма равна 180 градусам.
Какие примеры дополнительных углов можно привести?
Примерами дополнительных углов могут быть углы 30 градусов и 150 градусов, 45 градусов и 135 градусов, 60 градусов и 120 градусов и т.д.
Какие свойства имеют дополнительные углы?
Свойством дополнительных углов является то, что их сумма равна 180 градусам.
Для чего нужны дополнительные углы в математике?
Дополнительные углы используются для решения различных задач и проблем, связанных с геометрией и тригонометрией.
Как находить дополнительные углы
1. Если у вас есть один из дополнительных углов, то для нахождения второго угла нужно вычесть из 180 градусов известный угол. Например, если один угол равен 45 градусам, то второй угол будет равен 180 — 45 = 135 градусам.
2. Если у вас даны две линии, пересекающиеся, и один из углов при пересечении этих линий измеряется, то чтобы найти дополнительный угол, нужно от измеренного угла отнять 180 градусов. Например, если измеренный угол равен 60 градусам, то дополнительный угол будет равен 180 — 60 = 120 градусам.
3. Если у вас дан треугольник, в котором один из углов измеряется, то чтобы найти дополнительный угол, нужно от 180 градусов вычесть сумму измеренного угла и других углов треугольника. Например, если измеренный угол равен 45 градусам, а другие два угла треугольника равны 60 и 75 градусам, то дополнительный угол будет равен 180 — (45 + 60 + 75) = 180 — 180 = 0 градусов.
Важно помнить, что сумма дополнительных углов всегда равна 180 градусам. Это свойство можно использовать для решения различных задач и построения геометрических фигур.
Значение дополнительных углов в геометрии
Знание дополнительных углов позволяет делать различные выводы о свойствах и характеристиках геометрических фигур. Например, если два угла являются дополнительными, то мы можем сказать, что они смежные и образуют линейную пару углов.
Дополнительные углы могут быть использованы для нахождения неизвестных значений углов. Например, если мы знаем, что один угол равен 120 градусам, то второй угол будет равен 180 минус 120, то есть 60 градусов.
Кроме того, дополнительные углы встречаются в построении и измерении геометрических фигур. Например, при построении прямоугольника, сумма его углов должна быть равна 360 градусов. Это значит, что каждая пара противоположных углов прямоугольника будет являться дополнительными.
Таким образом, понимание и использование дополнительных углов в геометрии позволяет упростить решение задач, делать выводы о свойствах фигур и строить геометрические построения.
Применение дополнительных углов в реальной жизни
Понимание дополнительных углов имеет практическое применение в различных сферах нашей жизни. Ниже приведены примеры использования дополнительных углов:
1. Архитектура и строительство:
В архитектуре и строительстве знание дополнительных углов позволяет инженерам и архитекторам точно определить форму здания или сооружения и правильно расположить элементы конструкции. Например, при проектировании треугольной крыши необходимо знать дополнительные углы, чтобы правильно расположить стены и крышу.
2. Геодезия и навигация:
В геодезии и навигации дополнительные углы используются для определения направления движения или местоположения объектов на земле. Например, при использовании компаса для ориентирования в лесу, знание дополнительных углов помогает определить правильное направление и достичь цели.
3. Инженерия и машиностроение:
В инженерии и машиностроении дополнительные углы используются для правильной сборки и настройки механизмов и машин. Например, при сборке автомобиля или мотоцикла необходимо корректно установить углы поворота колес и углы наклона руля для обеспечения безопасности и оптимального функционирования транспортного средства.
4. Графический дизайн и искусство:
В графическом дизайне и искусстве дополнительные углы могут использоваться для создания сбалансированных и гармоничных композиций. Например, при создании логотипа или афиши важно учитывать дополнительные углы, чтобы элементы дизайна работали вместе и создавали единое целое.
Понимание дополнительных углов позволяет нам не только решать задачи в математике, но и применять эти знания в реальной жизни, повышая нашу эффективность и точность в различных областях деятельности.
Закономерности и особенности дополнительных углов
Закономерности дополнительных углов:
- Сумма дополнительных углов равна 180 градусам: Если даны два дополнительных угла, их сумма всегда будет равна 180 градусам. Например, если один угол равен 60 градусам, то второй угол будет равен 120 градусам.
- Углы-дополнения к одному и тому же углу равны: Если даны два угла, и их сумма равна 180 градусам, то каждый из этих углов является дополнением к другому углу. Например, если один угол равен 45 градусам, то второй угол также будет равен 135 градусам.
Особенности дополнительных углов:
- Дополнительные углы могут быть как острыми, так и тупыми: В зависимости от значений углов, дополнительные углы могут быть как острыми (меньше 90 градусов), так и тупыми (больше 90 градусов). Например, пара углов 30 градусов и 150 градусов является дополнительной, хотя один угол острый, а другой тупой.
- Дополнительные углы образуют линейную пару: Дополнительные углы лежат на одной прямой, образуя линейную пару. Это значит, что при расположении этих углов друг за другом они образуют прямую линию.
Понимание закономерностей и особенностей дополнительных углов помогает в решении задач геометрии и вычислении значений углов в различных конструкциях.
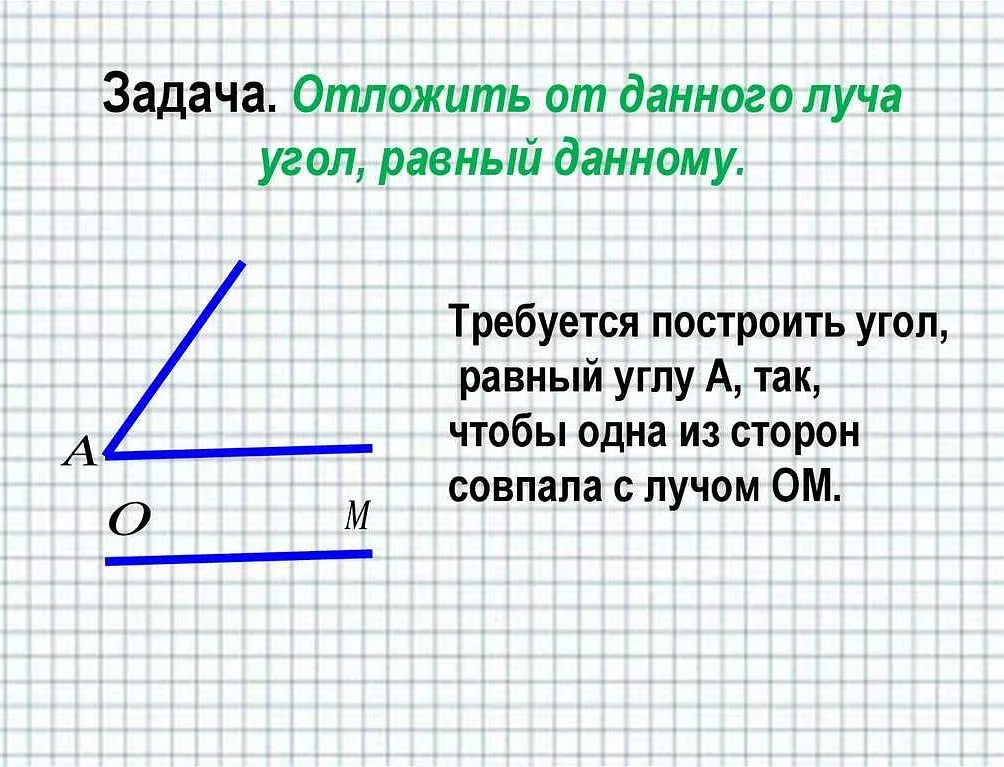



Дополнительные углы в математике — это такие углы, которые в сумме дают 180 градусов. Это понятие очень важно в геометрии, так как позволяет решать множество задач, связанных с углами и их взаимными отношениями. Для лучшего понимания этого понятия, рассмотрим пример. Представьте себе две прямые линии, пересекающиеся друг с другом. В месте их пересечения образуются четыре угла. Дополнительные углы — это две пары углов, которые находятся друг против друга и сумма каждой пары равна 180 градусов. Если угол А равен 60 градусов, то его дополнительный угол В будет равен 120 градусов. Это происходит потому, что сумма углов А и В равна 180 градусов. То же самое справедливо и для другой пары углов. Знание о дополнительных углах позволяет решать задачи, связанные с параллельными линиями и углами. Например, если две прямые линии пересекаются, то верхний левый угол и нижний правый угол будут дополнительными углами. В общем, понимание дополнительных углов является основой для решения многих геометрических задач. Это очень полезное знание не только для математики, но и для повседневной жизни.
Дополнительные углы в математике – это такие углы, которые в сумме дают 180 градусов. Они часто встречаются в геометрии и позволяют нам решать различные задачи, связанные с углами. Например, если у нас есть два угла, один из которых равен 60 градусов, то второй угол будет дополнительным и тоже будет равен 120 градусам (180 — 60 = 120). Также мы можем использовать это свойство, чтобы находить неизвестные углы. Если у нас есть прямая, пересекаемая другой прямой, то сумма двух смежных углов будет равна 180 градусам. Дополнительные углы очень полезны при решении задач по треугольникам, особенно если у нас уже есть известные углы. Они также помогают нам определить, является ли треугольник прямоугольным, остроугольным или тупоугольным. Математика – это наука, которая помогает нам понять окружающий нас мир. Понимание дополнительных углов поможет вам не только в учебе, но и в повседневной жизни, например, при строительстве или измерении углов. Поэтому не стоит пренебрегать изучением этой темы, она действительно полезна и интересна.
Отличная статья! Я всегда был немного запутан в определении дополнительных углов, но сейчас все стало на свои места. Теперь я понимаю, что дополнительные углы — это два угла, сумма которых равна 180 градусов. Это очень полезное понятие, которое можно применять в различных областях математики и физики. Прочитав примеры в статье, я увидел, как дополнительные углы могут быть использованы для решения различных задач. Например, если у нас есть угол, равный 60 градусам, то его дополнительный угол будет равен 120 градусам. Это знание может помочь нам расчитать углы в треугольниках или при решении геометрических задач. Я действительно нашел эту статью полезной и информативной. Теперь я чувствую себя увереннее в своих знаниях о дополнительных углах и готов применять их в своих математических расчетах. Спасибо за такую полезную информацию!
Статья очень понравилась! Всегда интересно узнавать что-то новое о математике. Я никогда раньше не слышал о понятии дополнительных углов, так что было интересно узнать, что это такое. Определение было очень четким и понятным, а примеры помогли мне лучше понять, как работать с этим понятием. Мне особенно понравился пример с углом в 60 градусов и его дополнительным углом в 120 градусов. Я никогда раньше не задумывался о том, что два угла могут быть дополнительными друг к другу. Теперь я понимаю, что дополнительные углы всегда в сумме дают 180 градусов, и это очень полезное знание. Статья была очень хорошо структурирована и легко читалась. Я часто сталкиваюсь с сложными математическими терминами, которые трудно понять, но здесь все было представлено просто и доступно. Спасибо за информативную и интересную статью! Буду ждать новых материалов на вашем сайте.