Что такое дт в математике
Содержимое
- 1 Что такое дт в математике
- 1.1 Понятие ДТ в математике
- 1.2 Видео по теме:
- 1.3 Определение ДТ в математике
- 1.4 Виды ДТ в математике
- 1.5 Примеры ДТ в математике
- 1.6 Основные свойства ДТ в математике
- 1.7 Значение ДТ в математике
- 1.8 Применение ДТ в математике
- 1.9 Выводы о ДТ в математике
- 1.10 Вопрос-ответ:
- 1.10.0.1 Что такое ДТ в математике?
- 1.10.0.2 Какие основные понятия входят в ДТ?
- 1.10.0.3 Зачем нужно изучать ДТ в математике?
- 1.10.0.4 Какие правила дифференцирования существуют?
- 1.10.0.5 Какова роль дифференциала в ДТ?
- 1.10.0.6 Какое определение имеет термин «ДТ» в математике?
- 1.10.0.7 Какие основные понятия связаны с ДТ в математике?
Дискретная математика — это раздел математики, который изучает объекты и явления, которые могут принимать только конечное или счетное количество значений. Дискретная математика широко применяется в компьютерной науке и информационных технологиях. В данной статье рассматривается понятие дискретности и ее применение в математике.
Дифференциальное исчисление, или ДТ, является одной из основных разделов математического анализа. Оно занимается изучением производных функций и их свойств. ДТ является важной математической теорией, которая широко применяется во многих областях науки и техники, включая физику, экономику, инженерное дело и компьютерные науки.
Основным понятием в ДТ является производная функции, которая показывает, как быстро функция меняется в каждой точке. Производная функции определяется как предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю. Производная функции может быть представлена как функция самого аргумента или как новая функция, называемая производной функции.
Производная функции имеет много важных свойств и применений. Например, она позволяет определить точки экстремума функции, то есть точки минимума или максимума. Производная также позволяет аппроксимировать функцию линейной функцией в малой окрестности точки, что является основой для численных методов решения математических задач.
Дифференциальное исчисление является неотъемлемой частью математического анализа и является ключевым инструментом для изучения функций и их свойств. Понимание основных понятий и результатов ДТ позволяет решать широкий спектр математических задач и применять их в различных областях науки и техники.
Понятие ДТ в математике

Дискретные пространства играют важную роль в математике и инженерии, так как многие реальные системы описываются дискретными значениями. Примерами дискретных пространств могут служить натуральные числа, булевы значения (0 или 1), а также конечные множества элементов.
Одним из важных понятий в ДТ является дискретная функция или последовательность. Дискретная функция определена на дискретном пространстве и сопоставляет каждому элементу этого пространства некоторое значение. Последовательность, в свою очередь, представляет собой упорядоченный набор элементов дискретного пространства.
Дискретное пространство также позволяет определить операции над его элементами, такие как сложение, вычитание, умножение и деление. Эти операции могут быть использованы для решения различных задач, связанных с дискретным пространством.
Изучение дискретных пространств и их свойств является важной областью математики, которая находит применение в различных областях науки и техники, таких как информатика, теория графов, криптография и др.
Видео по теме:
Определение ДТ в математике
Дифференциал — это малое приращение функции, которое можно рассматривать как линейным приближением к функции в окрестности данной точки. Производная — это отношение дифференциала функции к соответствующему приращению аргумента. Она показывает, как изменяется значение функции при изменении аргумента.
Производная функции может быть представлена в виде функции или таблицы значений, в которой каждой точке области определения функции сопоставляется ее производная. Производная может быть положительной, отрицательной или нулевой в зависимости от того, увеличивается или уменьшается значение функции в данной точке.
Дифференциальное исчисление широко применяется в физике, экономике, биологии и других науках для моделирования и анализа различных процессов и явлений. Оно позволяет решать задачи оптимизации, находить экстремумы функций, а также строить графики функций и исследовать их свойства.
Виды ДТ в математике
Существуют различные виды ДТ в математике, включая:
Вид ДТОписание
| Производная | Дифференциальная трансформация, показывающая скорость изменения функции в каждой точке. |
| Интеграл | Дифференциальная трансформация, обратная производной, позволяющая вычислить площадь под кривой или найти исходную функцию. |
| Градиент | Дифференциальная трансформация, определяющая направление наибольшего изменения функции в каждой точке. |
| Лапласиан | Дифференциальная трансформация, являющаяся суммой вторых производных функции и используемая в уравнениях математической физики. |
Каждый из этих видов ДТ имеет свои особенности и применяется в различных областях математики и науки. Знание этих трансформаций позволяет решать широкий спектр задач и моделировать различные явления.
Примеры ДТ в математике

Решение: Для нахождения производной функции f(x) нужно найти производную каждого слагаемого и сложить их. В данном случае, производная функции f(x) будет равна f'(x) = 2x + 5.
Пример 2: Дана система уравнений:
2x + y = 7
3x — 2y = 4
Решение: Для решения данной системы уравнений можно воспользоваться методом определителей. Найдем определители D, Dx и Dy:
D = (2 * -2) — (1 * 3) = -4 — 3 = -7
Dx = (7 * -2) — (1 * 4) = -14 — 4 = -18
Dy = (2 * 4) — (7 * 3) = 8 — 21 = -13
Теперь найдем значения x и y:
x = Dx / D = -18 / -7 = 18 / 7 ≈ 2.57
y = Dy / D = -13 / -7 = 13 / 7 ≈ 1.86
Таким образом, решение системы уравнений будет x ≈ 2.57, y ≈ 1.86.
Пример 3: Дано уравнение sin(x) + cos(x) = 1. Найти его решения.
Решение: Для нахождения решений данного уравнения можно воспользоваться тригонометрическими свойствами и привести его к виду sin(x) = 1 — cos(x). Затем можно воспользоваться таблицей значений для нахождения решений. Например, при x = 0, sin(x) = 0, а cos(x) = 1, что не удовлетворяет уравнению. При x = π/2, sin(x) = 1, а cos(x) = 0, что удовлетворяет уравнению. Таким образом, решение уравнения будет x = π/2.
Основные свойства ДТ в математике

Дискретное время – это множество, состоящее из точек, расположенных на числовой оси. Каждая точка дискретного времени соответствует определенному моменту времени. Например, множество натуральных чисел может быть использовано в качестве дискретного времени.
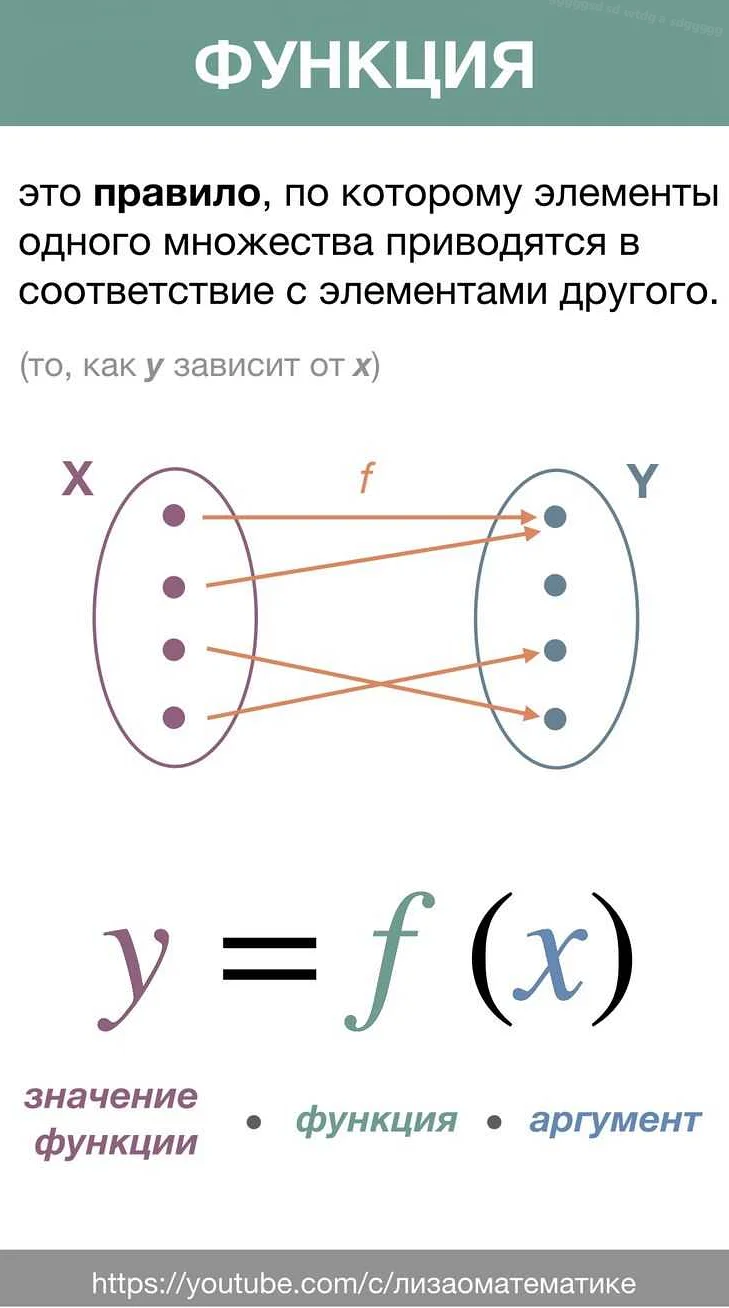
Функция в дискретном времени – это правило, которое ставит в соответствие каждой точке дискретного времени определенное значение. Такие функции обычно обозначаются как f(n), где n – точка дискретного времени.
Линейность – одно из основных свойств дискретной функции. Если f(n) и g(n) – две дискретные функции, а A и B – произвольные константы, то функция A*f(n) + B*g(n) также является дискретной функцией. Это означает, что дискретные функции можно складывать и умножать на константы.
Периодичность – еще одно свойство дискретных функций. Функция f(n) называется периодической с периодом N, если для любого целого n выполняется равенство f(n) = f(n + N). Таким образом, значение функции повторяется через каждые N точек дискретного времени.
Гармонический сигнал – это периодическая функция синусоидальной формы. Такой сигнал можно представить в виде f(n) = A*sin(ωn + φ), где A – амплитуда, ω – частота, φ – фазовый сдвиг.
Свертка – операция, которая позволяет совместить две функции в одну. Для дискретных функций f(n) и g(n) свертка определяется как f(n) * g(n) = Σf(k) * g(n — k), где Σ обозначает сумму по всем значениям k.
Корреляция – это мера сходства двух функций. Для дискретных функций f(n) и g(n) корреляция определяется как Corr(f, g) = Σf(k) * g(n + k), где Σ обозначает сумму по всем значениям k.
Значение ДТ в математике
Дифференциальный треугольник (ДТ) является одной из основных концепций дифференциального исчисления. Он представляет собой малый треугольник, который используется для изучения изменения функции на малом отрезке.
ДТ обычно обозначается символами Δx, Δy и δx, где Δx и Δy — это изменение аргумента и значения функции соответственно, а δx — бесконечно малое изменение аргумента.
Используя ДТ, можно определить производную функции, которая показывает скорость изменения функции в каждой точке. Производная функции вычисляется как предел отношения изменения значений функции к изменению аргумента, когда изменение аргумента стремится к нулю.
Дифференциальный треугольник помогает понять основные принципы дифференциального исчисления, а также применять их для решения различных задач, связанных с изменением функций.
Важно отметить, что ДТ является аппроксимацией, и его использование основывается на предположении, что функция достаточно гладкая и непрерывная. Более точные методы дифференцирования могут быть применены в более сложных случаях.
Применение ДТ в математике
Данное применение ДТ в математике позволяет решать различные задачи и проводить исследования с использованием численных методов. Основная идея ДТ заключается в замене непрерывных величин на дискретные, которые могут быть вычислены и обработаны с помощью компьютера.
Одно из основных применений ДТ в математике – это численное решение уравнений и систем уравнений. С помощью численных методов можно найти приближенное решение дифференциальных уравнений, а также найти корни уравнений и решить системы уравнений. Это позволяет решать задачи, для которых аналитическое решение может быть сложным или невозможным.
Еще одно применение ДТ в математике связано с аппроксимацией функций. С помощью численных методов можно приближенно представить сложные функции в виде простых аналитических выражений или интерполяционных полиномов. Это позволяет упростить вычисления и сделать их более эффективными.
Дискретное преобразование Фурье (ДПФ) является еще одним важным применением ДТ в математике. ДПФ позволяет анализировать и обрабатывать сигналы, представленные в виде дискретных отсчетов. С помощью ДПФ можно выделить спектральные составляющие сигнала, а также преобразовать его из временной области в частотную.
Также ДТ используется в численных методах оптимизации. С помощью ДТ можно найти экстремумы функций и оптимальные решения задач оптимизации. Это позволяет решать задачи поиска минимума или максимума функции, оптимального распределения ресурсов и другие задачи, связанные с оптимизацией.
Применение ДТ в математике широко распространено и находит свое применение в различных областях, включая науку, инженерию, физику, экономику и многие другие. Оно позволяет проводить сложные вычисления, анализировать данные и решать задачи, для которых аналитические методы могут быть неприменимыми или неэффективными.
Выводы о ДТ в математике

Основные понятия дифференциального исчисления включают производную функции, которая показывает скорость изменения функции в каждой точке, и дифференцируемую функцию, у которой существует производная в каждой точке ее области определения.
Дифференциальное исчисление находит широкое применение в различных областях науки и техники, таких как физика, экономика, инженерия и другие. Оно позволяет анализировать и оптимизировать сложные процессы, моделировать изменения и предсказывать будущие состояния систем.
Понимание и применение дифференциального исчисления позволяет нам лучше понять мир вокруг нас и улучшить наши навыки анализа и решения проблем. Оно является одной из основных основ математики и играет важную роль в развитии науки и технологий.
Вопрос-ответ:
Что такое ДТ в математике?
ДТ в математике означает дифференциальное исчисление и представляет собой раздел математического анализа, который изучает процесс нахождения производных функций.
Какие основные понятия входят в ДТ?
Основные понятия в дифференциальном исчислении включают понятие производной, правила дифференцирования, экстремумы функций, дифференциалы и дифференцируемость.
Зачем нужно изучать ДТ в математике?
Изучение дифференциального исчисления позволяет анализировать изменение функций, находить точки экстремума, определять скорость изменения величин, решать оптимизационные задачи и многое другое. Оно является основой для понимания и применения более сложных математических теорий и моделей.
Какие правила дифференцирования существуют?
В ДТ существуют различные правила дифференцирования, включая правило линейности, правило производной суммы, правило производной произведения, правило производной частного и многие другие. Они позволяют находить производные сложных функций и упрощать вычисления.
Какова роль дифференциала в ДТ?
Дифференциал в дифференциальном исчислении играет важную роль. Он представляет собой малое приращение функции и используется для аппроксимации изменения функции в окрестности данной точки. Дифференциалы позволяют записывать формулы и правила дифференцирования в более компактной и удобной форме.
Какое определение имеет термин «ДТ» в математике?
ДТ, или дифференциальное топологическое пространство, — это математическая структура, которая объединяет понятия топологии и анализа. В ДТ определены понятия непрерывности и дифференцируемости функций, а также введены понятия гладкости и касания.
Какие основные понятия связаны с ДТ в математике?
Основные понятия, связанные с ДТ в математике, включают понятия открытых и замкнутых множеств, непрерывности и дифференцируемости функций, сходимости последовательностей, компактности и связности пространства. Также в ДТ рассматриваются понятия предела и производной функции.


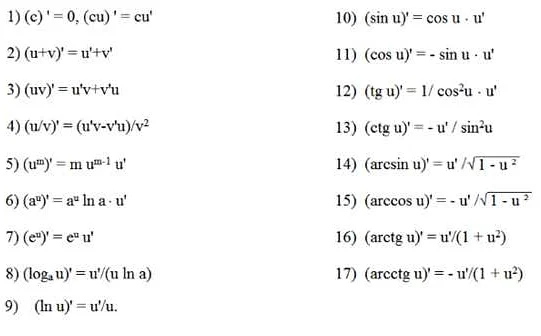
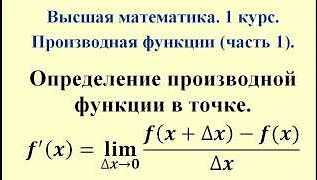
Интересная и познавательная статья! Я всегда интересовалась математикой, и теперь я наконец поняла, что такое ДТ. Дифференциальное исчисление — это метод, который позволяет нам изучать изменение функций и их свойств. Очень удобно, что с его помощью можно определить точку, в которой функция имеет максимум или минимум. Теперь, когда я знаю основные понятия и определения, я смогу легче разбираться в сложных математических задачах. Эта информация будет полезна не только в школе, но и в повседневной жизни. Спасибо за полезную статью!
Отличная статья! Всегда интересно погрузиться в мир математики и расширить свой кругозор. Я с удовольствием узнала, что такое ДТ в математике и какие основные понятия с ним связаны. Теперь я понимаю, что ДТ — это дискретный анализ, который занимается изучением дискретных объектов и явлений. Это очень важно в современном мире, где все больше данных становятся дискретными. Узнав, что такое алгоритмы и структуры данных, я поняла, что они помогают в обработке и хранении этих данных, что особенно актуально в информационных технологиях. Я также узнала о понятии графов, которые помогают представить и анализировать сложные системы. Все эти концепции кажутся мне очень интересными и полезными. Спасибо за такую информативную статью! Она помогла мне лучше понять, что такое ДТ в математике и какие понятия с ним связаны.
Статья очень хорошо объясняет, что такое ДТ в математике и какие понятия с ним связаны. Я всегда думала, что ДТ — это просто комплексные числа, но оказывается, это гораздо больше. Теперь я поняла, что ДТ — это система алгебраической геометрии, которая занимается изучением алгебраических кривых и их связей с комплексными числами. Прочитав статью, я поняла, что ДТ имеет множество применений в различных областях, таких как криптография и теория чисел. Очень интересно было узнать о понятии «сингулярности» и о том, как она связана с алгебраическими кривыми. Теперь я точно знаю, что такое ДТ и какие основные понятия с ним связаны. Спасибо за информативную статью!