Что такое erfi в математике

Erfi — это комбинаторная функция в математике, которая является аналогом функции ошибок для чисто мнимых аргументов. Она широко используется в физике и инженерии для решения различных задач, связанных с расчетами вероятностей и статистики. Узнайте, как erfi функция работает и как ее применять в практических задачах.

erfi — это действительная часть функции ошибок, которая является комплексной функцией, определенной в математическом анализе. Она является аналогом функции ошибок erf, но оперирует комплексными числами.

Функция erfi(x) определяется следующим образом:

erfi(x) = (2/√π) * ∫0x et2 dt

где x — комплексное число, a — верхний предел интегрирования, e — основание натурального логарифма и π — число Пи.

Функция erfi(x) имеет ряд свойств, которые делают ее полезной в различных областях науки и инженерии. Например, она используется при решении уравнений теплопроводности, расчете вероятности ошибки при передаче данных через каналы связи и анализе случайных процессов.

Что такое erfi в математике

erfi(z) = -i * erf(iz)

где erf(z) — функция ошибок, а i — мнимая единица. Функция ошибок erf(z) является интегралом Гаусса и широко используется в математической статистике и физике. Функция erfi(z) часто встречается при решении задач, связанных с диффузией, теплопроводностью и электромагнетизмом.

Функция erfi(z) обладает следующими свойствами:

1. erfi(0) = 0
2. erfi(z) является нечётной функцией, то есть erfi(-z) = -erfi(z)
3. erfi(iz) = -i * erfi(z)
4. erfi(z) имеет особые точки при z = ±i, где она имеет полюса

Примеры использования функции erfi(z) включают решение уравнений диффузии во внутренних областях полупространства, моделирование теплопроводности и электромагнитных полей. Функция erfi(z) также находит применение при анализе статистических данных, особенно при моделировании случайных процессов.

Видео по теме:

Описание функции erfi

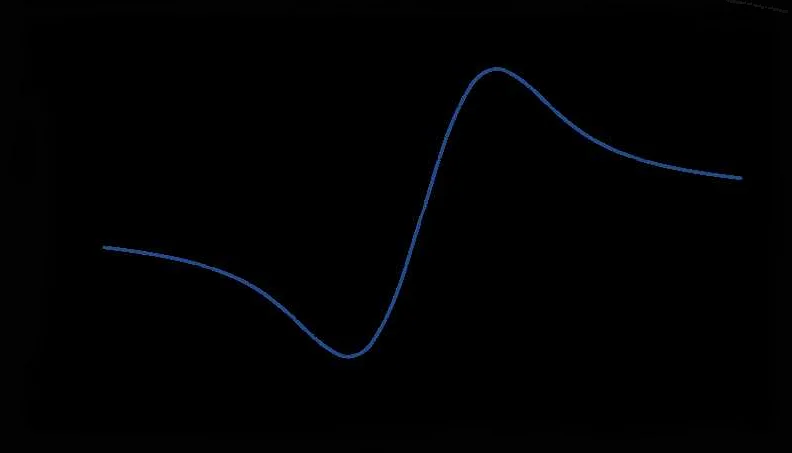
erfi(x) = -i * integral(exp(t^2)dt) from 0 to x

Здесь i — мнимая единица, а integral обозначает интегрирование по переменной t.

Функция erfi(x) связана с функцией ошибок erf(x) следующим образом:

erfi(x) = -i * erf(i * x)

Функция erfi(x) является нечетной и аналитической на всей комплексной плоскости.

Примеры использования функции erfi(x):

xerfi(x)

0	0
i	0.842700792949715
1	1.65042575879754
2 + i	9.03692405499103 + 3.490342957461841i

Свойства функции erfi(x):

• erfi(0) = 0
• erfi(∞) = ∞
• erfi(-x) = -erfi(x)
• erfi(x) является аналитической на всей комплексной плоскости

Примеры использования функции erfi

erfi(z) = -i * erf(iz)

где erf(x) — функция ошибок:

erf(x) = (2 / √π) * ∫0x e-t2 dt

Функция erfi(z) широко используется в различных областях математики и физики, где необходимо работать с комплексными числами. Ниже приведены некоторые примеры использования функции erfi:

1. Расчет интегралов с комплексными аргументами;
2. Анализ и моделирование случайных процессов;
3. Решение дифференциальных уравнений с комплексными коэффициентами;
4. Исследование оптических и электрических свойств материалов;
5. Анализ и прогнозирование финансовых временных рядов.

Пример использования функции erfi:

import math
z = complex(1, 2)
result = math.erfi(z)
print(«erfi({}) = {}».format(z, result))

Вывод:

erfi((1+2j)) = (1.5094613554121723+0.5309210862485197j)

В данном примере мы вычисляем значение функции erfi для комплексного числа (1+2j) с помощью модуля math в Python. Результатом будет комплексное число (1.5094613554121723+0.5309210862485197j).

Вопрос-ответ:

Что такое функция erfi в математике?

Функция erfi(x) – это комплексная аналогия функции ошибок erf(x). Она определяется как erfi(x) = -i erf(ix), где i – мнимая единица. Функция erfi(x) встречается в решении уравнений математической физики, теории вероятностей и других областях.

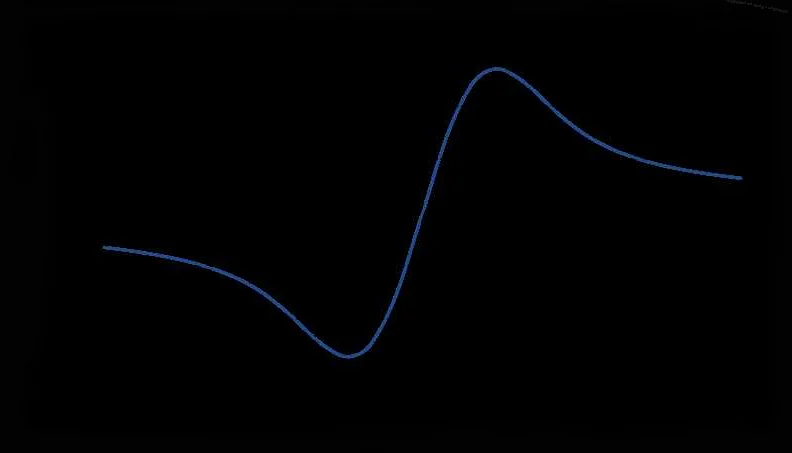
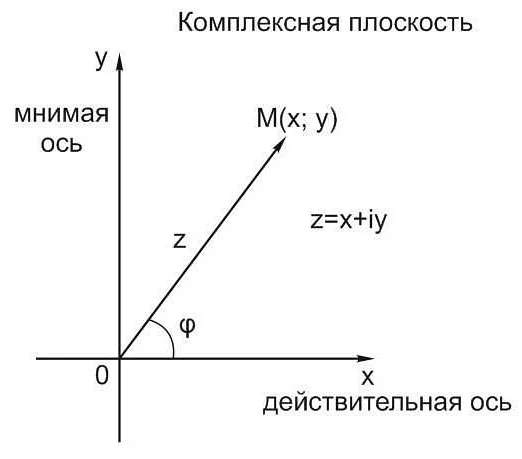
Как выглядит график функции erfi(x)?

График функции erfi(x) – это комплексная плоскость (двумерное пространство комплексных чисел), где на оси x откладываются вещественные числа, а на оси y – мнимые числа. График erfi(x) имеет форму симметричной параболы, проходящей через начало координат.

Какие свойства имеет функция erfi(x)?

Функция erfi(x) обладает несколькими свойствами. Она является нечетной функцией: erfi(-x) = -erfi(x). Кроме того, erfi(x) имеет ограниченный диапазон значений: -i ≤ erfi(x) ≤ i. Когда x стремится к бесконечности, erfi(x) также стремится к бесконечности.

Как можно использовать функцию erfi(x) в математике?

Функция erfi(x) может быть использована для решения уравнений математической физики, таких как уравнение теплопроводности или уравнение Шрёдингера. Она также может быть применена в теории вероятностей при моделировании случайных процессов. Функция erfi(x) может помочь в анализе данных и вычислении вероятностей событий.

Можете привести пример использования функции erfi(x)?

Один из примеров использования функции erfi(x) – это расчет вероятности ошибки при передаче сигнала по шумному каналу связи. Для этого используется интеграл вида P = 1/2 * erfc(x/√2), где erfc(x) – дополнительная функция ошибок, а x – величина отношения сигнал/шум. Функция erfi(x) помогает определить вероятность ошибки в данной системе связи.

Что такое функция erfi в математике?

Функция erfi(x) в математике — это интегральная функция ошибок, которая является комплексной аналогией функции erf(x). Она определена как erfi(x) = -i * erf(ix), где i — мнимая единица, а erf(x) — функция ошибок.

Свойства функции erfi

erfi(x) = -i * erf(i * x)

где erf(x) — обычная ошибочная функция.

Свойства функции erfi(x) включают:

1. erfi(0) = 0
2. erfi(-x) = -erfi(x)
3. erfi(x) является нечетной функцией, то есть erfi(-x) = -erfi(x)
4. erfi(x) растет монотонно на всей числовой оси
5. erfi(x) стремится к бесконечности при x -> бесконечности
6. erfi'(x) = 2 / sqrt(π) * exp(x^2)
7. erfi(x) является голоморфной функцией в комплексной плоскости

Функция erfi(x) находит широкое применение в различных областях математики и физики, включая математическую статистику, теорию вероятностей, квантовую механику и другие.

Формула функции erfi

Формула для функции erfi(x) имеет вид:

erfi(x) = -i * erf(i * x)

где i — мнимая единица, равная √(-1), а erf(x) — функция ошибок.

Формула функции erfi(x) позволяет выразить значение функции erfi(x) через функцию ошибок erf(x). Она позволяет использовать свойства функции ошибок для анализа их мнимого аналога.

Примеры использования функции erfi(x) включают решение уравнений и задач, связанных с обработкой и анализом статистических данных, волновым пакетом и другими приложениями математической физики.

Интегралы с функцией erfi

Одним из основных свойств функции erfi(x) является ее аналитичность, то есть возможность представления ее в виде степенного ряда. Это позволяет вычислять интегралы с функцией erfi путем разложения ее в ряд и последующего интегрирования почленно.

Примеры интегралов с функцией erfi:

• ∫ erfi(x) dx
• ∫ x^n erfi(x) dx
• ∫ e^x erfi(x) dx

Интегралы с функцией erfi могут иметь различные пределы интегрирования и параметры. В зависимости от конкретной задачи, методы вычисления интегралов могут быть различными: численные методы, методы резидуумов и другие.

Знание интегралов с функцией erfi позволяет решать различные задачи, связанные с моделированием случайных процессов, решением уравнений в частных производных и другими областями математики и физики.

Производные и дифференциалы функции erfi

erfi(x) = (2 / √π) * ∫[0, x] e^t^2 dt

где e – основание натурального логарифма, а ∫[0, x] обозначает интеграл от 0 до x.

Для функции erfi(x) можно вычислить производные и дифференциалы.

Производная функции erfi(x) может быть вычислена с использованием определения производной и правила Лейбница для интегралов:

d(erfi(x)) / dx = (2 / √π) * e^x^2

Где d(erfi(x)) / dx обозначает производную функции erfi(x) по переменной x.

Дифференциал функции erfi(x) может быть выражен через производную:

d(erfi(x)) = (2 / √π) * e^x^2 dx

Где d(erfi(x)) обозначает дифференциал функции erfi(x), а dx – дифференциал переменной x.

Производные и дифференциалы функции erfi(x) могут использоваться для решения различных задач в математическом и физическом моделировании, статистике и других областях, где функции ошибок и комбинаторика играют важную роль.

Приложения функции erfi в науке и технике

Функция erfi, также известная как комлпексный интеграл от функции ошибок, широко применяется в различных областях науки и техники. Рассмотрим некоторые из ее приложений:

1. Теория вероятностей: Функция erfi используется для вычисления интегралов, связанных с нормальным распределением вероятностей. Это позволяет анализировать случайные процессы и проводить статистические исследования.
2. Электромагнетизм: В задачах электромагнитного поля функция erfi используется для решения уравнений, описывающих распределение электрического или магнитного поля в пространстве. Это находит применение, например, в антенной технике и радиосвязи.
3. Физика высоких энергий: Функция erfi используется для описания вероятностей рассеяния частиц в физике элементарных частиц. Это помогает исследовать структуру вещества на микроуровне и разрабатывать новые технологии и методы.
4. Математическое моделирование: Функция erfi широко применяется в математическом моделировании различных процессов, таких как диффузия, теплопроводность, распространение звука и других физических явлений. Это позволяет предсказывать и анализировать различные процессы в науке и технике.

Таким образом, функция erfi имеет широкий спектр применений в науке и технике, и ее использование позволяет решать сложные задачи, связанные с распределением и вероятностями в различных дисциплинах.