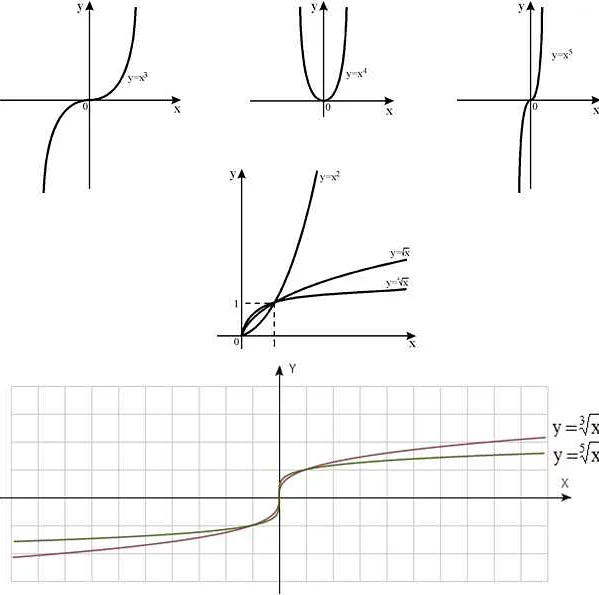
Что называют функцией в математике

Функция в математике — это математическое понятие, которое описывает зависимость между двумя множествами, где каждому элементу одного множества сопоставлен ровно один элемент другого множества. Узнайте о том, как функции используются в математике и как они могут быть представлены графически и символьно.

Функция является одним из основных понятий в математике. Это отношение, которое устанавливает соответствие между элементами двух множеств, таким образом, что каждому элементу из одного множества сопоставляется ровно один элемент из другого множества. Функции помогают структурировать и описывать зависимости между различными значениями.

Функции широко применяются в различных областях математики, а также в науке и технике. Они позволяют решать задачи, связанные с моделированием, анализом и прогнозированием. Определение функции включает в себя два основных элемента: область определения, которая содержит все значения, для которых функция определена, и область значений, которая содержит все возможные значения функции.

Примером функции может служить линейная функция. Она представляет собой функцию вида y = kx + b, где k и b — это константы, определяющие наклон и сдвиг графика. Данная функция устанавливает соответствие между значениями x и соответствующими значениями y на плоскости. Каждому значению x сопоставляется ровно одно значение y. Таким образом, линейная функция является примером функции в математике.

Важно отметить, что функция может быть представлена не только в аналитической форме, но и в графическом виде, таблице значений или словесно. Независимо от представления, функция остается основным инструментом для изучения и описания математических явлений и закономерностей.

Определение функции в математике

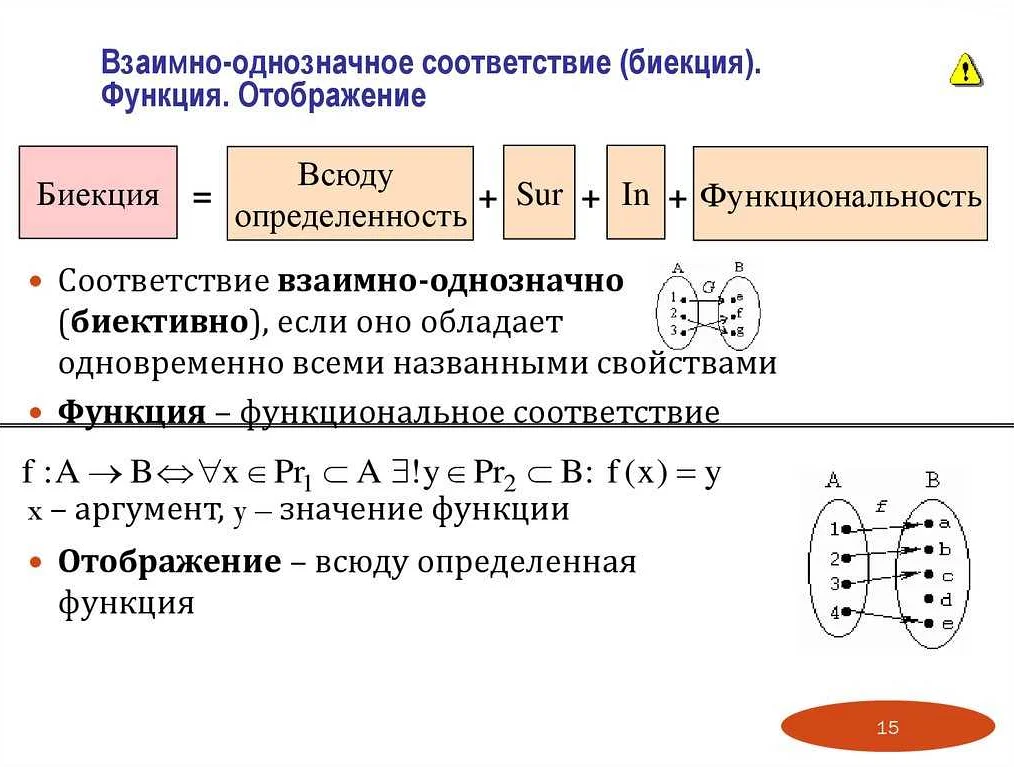
Множество, из которого выбираются элементы, называется областью определения функции. Множество, в которое отображаются элементы, называется областью значений функции.

Функция в математике обозначается следующим образом:

Область определенияОбласть значенийОбозначение функции

A

B

f: A → B

Определение функции включает в себя два важных условия:

1. Каждому элементу из области определения соответствует только один элемент из области значений.
2. Для каждого элемента из области определения должно быть определено значение в области значений.

Примеры функций в математике включают простые функции, такие как линейные функции, квадратные функции, тригонометрические функции, а также более сложные функции, такие как экспоненциальные и логарифмические функции.

Что такое функция

Функции в математике часто обозначают с использованием символов. Например, f(x) — функция, где x является переменной, а f(x) — результат функции для значения x. Математическое определение функции включает в себя три основных составляющих: область определения, область значений и правило, по которому происходит преобразование элементов из области определения в элементы области значений.

Функции широко используются в математике для моделирования различных явлений и процессов. Они позволяют математикам описывать и анализировать различные зависимости и взаимодействия между переменными. Функции являются важным инструментом для решения уравнений, оптимизации, построения графиков и многих других задач.

Математическое определение функции

Функция задается формулой или алгоритмом, который позволяет вычислить значение функции для каждого элемента из области определения.

Математическое определение функции имеет следующий вид:

Пусть X и Y — два непустых множества. Функция f: X -> Y — это соответствие, при котором каждому элементу x из множества X сопоставляется ровно один элемент y из множества Y.

Область определения функции — это множество всех элементов x из множества X, для которых существует соответствующий элемент y из множества Y.

Область значений функции — это множество всех элементов y из множества Y, которые являются результатом применения функции к элементам области определения.

Пример:

Рассмотрим функцию f(x) = x^2.

В данном случае, область определения функции — множество всех действительных чисел, так как для любого действительного числа x можно вычислить квадрат этого числа.

Область значений функции — множество неотрицательных действительных чисел, так как квадрат любого действительного числа неотрицателен.

Например, значение функции f(2) = 2^2 = 4.

Таким образом, математическое определение функции позволяет формально описать соответствие между элементами двух множеств и установить связь между областью определения и областью значений функции.

Графическое представление функции

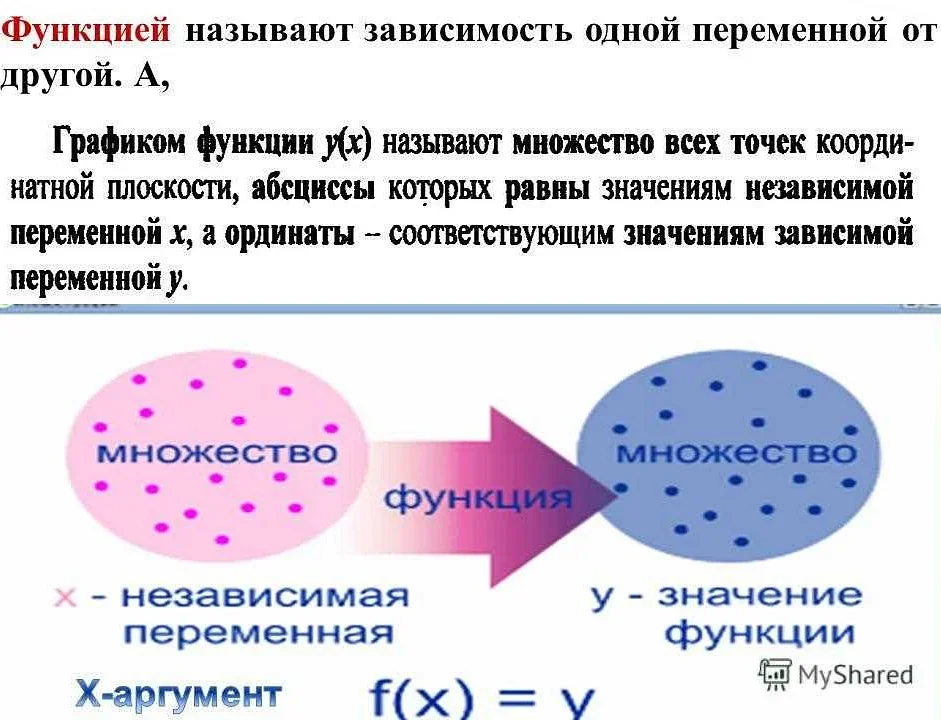
График функции представляет собой набор точек на плоскости, где каждой точке соответствует значение функции при заданном аргументе. Обычно график функции изображается на координатной плоскости, где ось абсцисс соответствует аргументу функции, а ось ординат — значению функции. Таким образом, каждая точка на графике имеет координаты (x, y), где x — значение аргумента, y — значение функции.

Графическое представление функции позволяет наглядно увидеть ее основные свойства, такие как область определения и значения, точки максимума и минимума, асимптоты и пересечения с осями координат. Также график функции позволяет сравнивать различные функции и исследовать их взаимное влияние.

Например, для функции y = f(x) = x^2 график будет представлять собой параболу, открывшуюся вверх. При увеличении значения аргумента x, значение функции y будет увеличиваться. График будет иметь вершину в точке (0, 0) и будет симметричен относительно оси ординат.

Графическое представление функции в математике позволяет легко анализировать ее свойства и использовать ее в решении различных задач, например, в оптимизации, физике, экономике и других областях науки.

Примеры функций

В математике существует множество различных примеров функций. Давайте рассмотрим несколько из них:

1. Функция f(x) = x^2:
   • Данная функция возвращает квадрат значения аргумента;
   • Например, при x = 2, f(2) = 4;
   • При x = -3, f(-3) = 9.
2. Функция g(x) = 2x + 3:
   • Данная функция возвращает результат умножения аргумента на 2 и прибавления к нему 3;
   • Например, при x = 4, g(4) = 11;
   • При x = -2, g(-2) = -1.
3. Функция h(x) = sin(x):
   • Данная функция возвращает синус аргумента;
   • Например, при x = π/2, h(π/2) = 1;
   • При x = π, h(π) = 0.

Это только некоторые примеры функций, которые используются в математике. Функции могут быть очень разнообразными и применяться в различных областях науки и техники.

Линейная функция

Линейная функция имеет график в виде прямой линии на координатной плоскости. Коэффициент k называется наклоном прямой, а коэффициент b – свободным членом. Наклон определяет, насколько быстро меняется значение функции y при изменении значения переменной x.

Примером линейной функции может служить функция y = 2x + 3. В данном случае наклон прямой равен 2, а свободный член равен 3. Зная значения переменной x, можно легко вычислить соответствующее значение функции y.

Линейная функция имеет множество применений в различных областях, таких как физика, экономика, инженерия и др. Она помогает описывать и предсказывать зависимости между двумя переменными.

Квадратичная функция

Коэффициент a определяет направление открывания параболы и влияет на ее «крутизну». Если a больше нуля, парабола будет открываться вверх, а если a меньше нуля, парабола будет открываться вниз. Коэффициент b влияет на смещение параболы по оси x, а коэффициент c определяет смещение параболы по оси y.

Примеры квадратичных функций:

1. f(x) = x^2 — квадратичная функция с вершиной в начале координат и открыванием параболы вверх.
2. f(x) = -2x^2 + 3x — 1 — квадратичная функция с вершиной в точке (0.75, -1.625) и открыванием параболы вниз.
3. f(x) = 4x^2 — 2x + 5 — квадратичная функция с вершиной в точке (0.25, 5.125) и открыванием параболы вверх.

Квадратичные функции широко используются в математике, физике, экономике и других областях для моделирования различных процессов и явлений. Изучение квадратичных функций позволяет анализировать и предсказывать их свойства и поведение в различных ситуациях.

Тригонометрическая функция

Существует несколько основных тригонометрических функций:

• Синус (sin): отношение противоположной стороны к гипотенузе.
• Косинус (cos): отношение прилежащей стороны к гипотенузе.
• Тангенс (tan): отношение синуса к косинусу.
• Котангенс (cot): отношение косинуса к синусу.
• Секанс (sec): отношение гипотенузы к прилежащей стороне.
• Косеканс (csc): отношение гипотенузы к противоположной стороне.

Тригонометрические функции широко применяются в различных областях науки и техники, таких как физика, инженерия, геометрия, астрономия и другие.

Вопрос-ответ:

Что такое функция в математике?

Функция в математике — это отношение между двумя множествами, где каждому элементу из первого множества соответствует единственный элемент из второго множества. Функция может быть представлена графически в виде графика, который показывает зависимость значений функции от ее аргументов.

Какие примеры функций можно привести?

В математике есть множество примеров функций. Например, линейная функция y = kx + b, где k и b — константы, а x — переменная, определяет прямую линию на координатной плоскости. Еще один пример — квадратная функция y = ax^2 + bx + c, где a, b и c — константы, а x — переменная, определяет параболу. Также существуют тригонометрические функции, экспоненциальные функции и много других видов функций.

Как определить, является ли заданное отношение функцией?

Для того чтобы определить, является ли заданное отношение функцией, нужно проверить, что каждому элементу из первого множества соответствует единственный элемент из второго множества. Если есть хотя бы один элемент, для которого это условие не выполняется, то отношение не является функцией.

Какие свойства имеют функции?

Функции обладают несколькими важными свойствами. Одно из них — единственность значений. Это означает, что каждому элементу из первого множества соответствует только один элемент из второго множества. Еще одно свойство — определенность значений. Это означает, что для каждого элемента из первого множества функция должна быть определена, то есть иметь значение во втором множестве. Также функции могут быть инъективными (взаимно однозначное соответствие), сюръективными (полное соответствие) или биективными (инъективные и сюръективные одновременно).

Как использовать функции в реальной жизни?

Функции находят широкое применение в реальной жизни. Например, они используются в финансовой математике для моделирования доходности инвестиций или оценки рисков. Также функции используются в физике для описания законов движения и в экономике для моделирования рыночных процессов. В общем, функции позволяют анализировать, предсказывать и оптимизировать различные процессы в разных областях науки и жизни.

Что такое функция в математике?

В математике функция — это отношение между двумя множествами, где каждому элементу первого множества соответствует ровно один элемент второго множества. Функция описывает зависимость между входными и выходными значениями.

Производная функции

Математически, производная функции обозначается как f'(x) или dy/dx и определяется как предел отношения изменения значения функции к изменению ее аргумента при стремлении последнего к нулю:

f'(x) = lim(h -> 0) (f(x + h) — f(x)) / h

Таким образом, производная функции показывает, насколько быстро значение функции меняется при изменении ее аргумента. Если производная положительна, то функция возрастает, если отрицательна — функция убывает, а если равна нулю — функция имеет экстремум (максимум или минимум).

Производная функции имеет множество приложений в различных областях, таких как физика, экономика, статистика и другие. Она позволяет анализировать и предсказывать поведение функций в зависимости от изменения их аргументов.

Видео по теме: