Математика 6кл что такое хорда

В математике, хорда — это отрезок, соединяющий две точки на окружности. Узнайте, как определить и использовать хорды в 6-м классе математики.

Хорда — это линия, которая соединяет две точки на окружности. В математике 6 класса изучается геометрия, в рамках которой хорда является одним из важных понятий. Хорда играет важную роль в определении других геометрических объектов и связей.

Когда две точки окружности соединены линией, получается хорда. Хорда может проходить через центр окружности или быть параллельной касательной. В зависимости от своего положения, хорда может быть диаметром или просто хордой, не являющейся диаметром.

Например, если провести линию, соединяющую точки A и B на окружности, получится хорда AB. Если эта хорда проходит через центр окружности, она является диаметром. Если она не проходит через центр, то это просто хорда.

Хорда обладает рядом свойств и характеристик, которые изучаются в математике 6 класса. Например, хорда делит окружность на две дуги. Каждая дуга окружности, ограниченная хордой, имеет свою длину и угол.

Определение и свойства хорды

Основное свойство хорды заключается в том, что она разделяет окружность на две дуги. Дуги, ограниченные хордой, называются дугами хорды. Дуги хорды, находящиеся по разные стороны от хорды, называются полудугами хорды.

Хорда, проходящая через центр окружности, называется диаметром. Диаметр является наибольшей хордой в окружности и делит ее на две равные части. Длина диаметра равна удвоенному радиусу окружности.

Другое важное свойство хорды заключается в том, что если две хорды в окружности равны, то их расстояния от центра окружности также равны. Таким образом, если две хорды имеют равную длину, то их расстояния от центра окружности будут равны между собой.

Отличия хорды от дуги

Отличия между хордой и дугой можно понять, рассмотрев их геометрические свойства.

ХордаДуга

Хорда является прямым отрезком, который соединяет две точки на окружности.	Дуга представляет собой часть окружности, лежащую между двумя конечными точками.
Хорда полностью лежит внутри окружности.	Дуга может быть как полной окружностью, так и ее частью.
Длина хорды всегда меньше или равна длине окружности.	Длина дуги зависит от ее угла и радиуса окружности.
Хорда может быть прямой или кривой.	Дуга всегда кривая.

Таким образом, хорда и дуга — это различные геометрические объекты, связанные с окружностью, каждый из которых имеет свои уникальные свойства и характеристики.

Как находить длину хорды

1. Если известна длина радиуса и угол, под которым хорда вписана в окружность, то длина хорды может быть найдена с использованием формулы:

L = 2 * r * sin(a/2)

где L — длина хорды, r — радиус окружности, a — угол в радианах.

2. Если известны координаты начальной и конечной точек хорды, то длина хорды может быть найдена с использованием формулы расстояния между двумя точками:

L = sqrt((x2 — x1)^2 + (y2 — y1)^2)

где L — длина хорды, (x1, y1) — координаты начальной точки хорды, (x2, y2) — координаты конечной точки хорды.

3. Если хорда является диаметром окружности, то ее длина равна длине диаметра и может быть найдена по формуле:

L = 2 * r

где L — длина хорды, r — радиус окружности.

Таким образом, нахождение длины хорды зависит от известных данных о радиусе окружности, угле, координатах точек или типе хорды.

Примеры задач с хордами

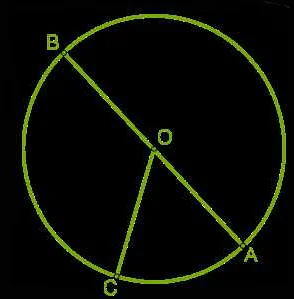
1. Найдите длину хорды, если радиус окружности равен 5 см, а угол, натянутый на эту хорду, равен 60 градусов.

2. В окружности диаметром 12 см проведена хорда, равная по длине радиусу окружности. Найдите длину этой хорды.

3. В окружности диаметром 10 см проведена хорда, равная по длине радиусу окружности. Найдите расстояние от центра окружности до этой хорды.

4. Вычислите площадь сектора, если радиус окружности равен 8 см, а длина хорды, натянутой на этот сектор, равна 12 см.

5. В окружности с радиусом 6 см проведена хорда, равная по длине 8 см. Найдите расстояние от центра окружности до середины этой хорды.

Виды хорд

В математике существуют различные виды хорд, которые можно классифицировать в зависимости от их свойств:

Вид хордыОписание

Диаметр	Хорда, проходящая через центр окружности. Диаметр является наибольшей хордой и делит окружность на две равные дуги.
Радиус	Хорда, соединяющая центр окружности с любой точкой на окружности.
Секущая	Хорда, которая пересекает окружность в двух точках.
Тангента	Хорда, которая касается окружности в точке, не пересекая ее.

Это основные виды хорд, которые встречаются в математике и играют важную роль в изучении геометрии окружностей.

Видео по теме:

Вопрос-ответ:

Что такое хорда?

Хорда — это отрезок, соединяющий две точки на окружности.

Как найти длину хорды?

Длина хорды может быть найдена с помощью формулы L = 2Rsin(α/2), где L — длина хорды, R — радиус окружности, α — центральный угол, под которым занимает хорда.

Какие свойства имеет хорда?

Хорда имеет несколько свойств: она является отрезком, она соединяет две точки на окружности, она может быть диаметром окружности, и она может быть частью дуги окружности.

Какова роль хорды в геометрии?

Хорда играет важную роль в геометрии, так как она позволяет определить много свойств и параметров окружности. Она используется для вычисления длин дуг и для нахождения центра окружности.

Как можно использовать понятие хорды в повседневной жизни?

Понятие хорды может быть использовано в повседневной жизни в различных ситуациях, например, при расчете длины троса или каната, необходимого для соединения двух точек на разных высотах.

Что такое хорда?

Хорда — это отрезок, соединяющий две точки на окружности.

Применение хорд в геометрии

Одно из применений хорд — нахождение расстояния между точками на окружности. Для этого можно использовать теорему о хордах, которая гласит: «Расстояние между точками на окружности равно длине хорды, соединяющей эти точки». Таким образом, если известна длина хорды и нужно найти расстояние между точками на окружности, можно использовать эту теорему.

В геометрических построениях также часто используются хорды. Например, для построения равнобедренного треугольника иногда можно использовать хорды, проведенные из вершин треугольника к основанию. Также хорды могут быть использованы для построения центра окружности, проведению касательных и других геометрических конструкций.

Важно помнить, что хорды имеют свои свойства, которые могут быть использованы при решении задач. Например, свойства равенства хорд при равенстве соответствующих дуг или углов.

Таким образом, хорды играют значимую роль в геометрии и имеют широкое применение при решении различных задач и построений.

Связь хорды с дугой и радиусом

Если мы проведем хорду в окружности, она будет разбивать дугу на две части. Дуга, ограниченная хордой, называется дугой хорды. При этом, хорда и дуга хорды имеют одну и ту же длину.

Связь хорды с радиусом проявляется в так называемом «правиле хорд». Если из центра окружности мы проведем две радиуса, пересекающие хорду, то получим два равных отрезка. То есть, радиусы, перпендикулярные к хорде, делят ее на две равные части.

Эти связи хорды с дугой и радиусом позволяют нам проводить различные геометрические рассуждения и доказательства в задачах, связанных с окружностями.