Что такое хорда в математике

Хорда в математике — это сегмент прямой линии, соединяющий две точки на окружности. Она играет важную роль в геометрии и тригонометрии, и используется для решения различных задач и вычислений. Узнайте, как определить хорду, вычислить ее длину и использовать ее в геометрических расчетах.

Хорда — это отрезок, соединяющий две точки на окружности. В математике хорда является одним из основных понятий геометрии и имеет широкий спектр применений.

Одно из ключевых свойств хорды — ее длина, которая определяется расстоянием между двумя точками. Другая важная характеристика хорды — ее положение относительно центра окружности. Если хорда проходит через центр, она называется диаметром. Диаметр является наибольшей хордой и делит окружность на две равные части.

Пример использования хорды в математике может быть представлен в геометрии. Например, при решении задач на построение. Зная длину хорды и ее положение на окружности можно построить треугольник, квадрат или другую фигуру.

Также хорда находит применение в алгебре и анализе. В алгебре хорда может быть использована для определения различных параметров окружности, таких как радиус, диаметр, длина дуги и площадь сектора. В анализе хорда может быть использована для построения графиков функций и решения уравнений.

Хорда — это важное понятие в математике, которое находит широкое применение в различных областях. Понимание основных свойств и применений хорды позволяет решать разнообразные задачи и проводить точные вычисления.

Основные понятия хорды в математике

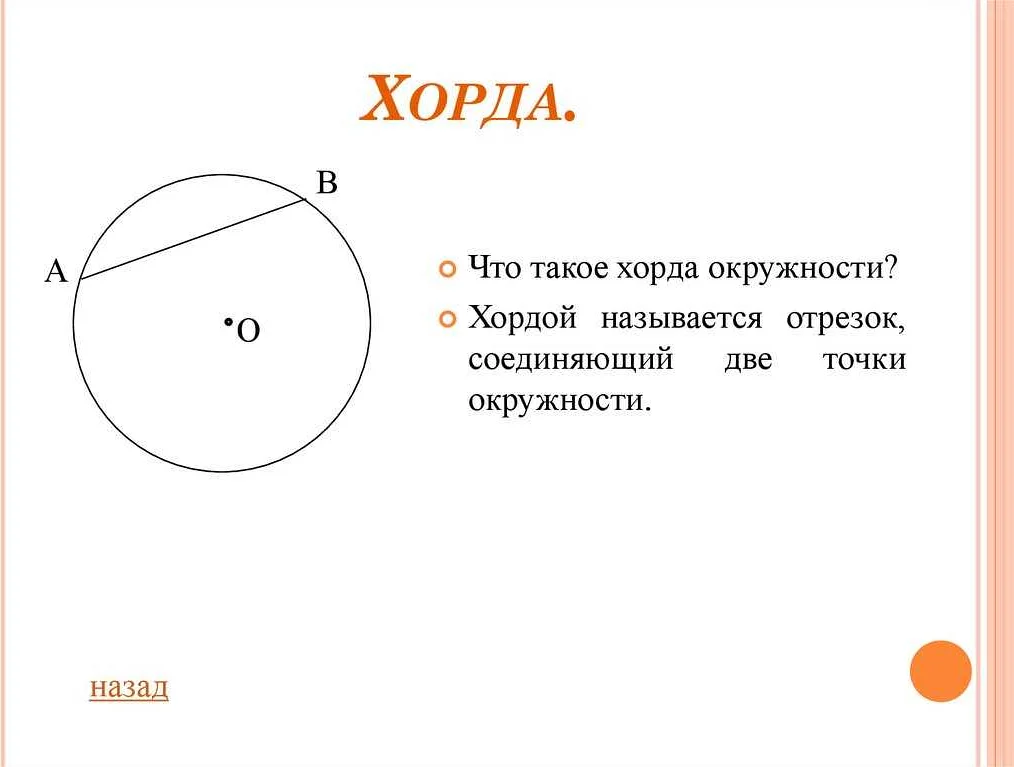
Длина хорды является одним из основных понятий, связанных с этой фигурой. Она измеряется в единицах длины, таких как сантиметры или метры.

Важным свойством хорды является то, что её длина может быть использована для вычисления других характеристик окружности. Например, длина хорды может быть использована для вычисления радиуса или площади окружности.

Хорды также играют важную роль в геометрии и аналитической геометрии. Они используются для определения различных геометрических фигур, таких как сегменты и дуги окружности.

Кроме того, хорды имеют важное значение в музыке. В музыкальных терминах хорда обозначает совместное звучание нескольких звуков, составляющих гармоническое целое.

В заключение, понятие хорды является основным в математике и имеет множество применений в различных областях знания.

Видео по теме:

Определение хорды и ее свойства

Основное свойство хорды заключается в том, что она является кратчайшим путем между двумя точками на окружности. Другими словами, любая другая кривая, соединяющая эти две точки (например, дуга окружности или дуга эллипса), будет иметь большую длину, чем хорда.

Хорды могут быть пересекающимися или непересекающимися. Если хорды пересекаются внутри окружности, то точка пересечения называется точкой пересечения хорд. Если хорды не пересекаются, то они называются параллельными хордами.

Еще одним важным свойством хорды является то, что она делит окружность на две дуги. Дуги, образованные хордой, называются дугами хорды. Дуги хорды могут быть равными или неравными по длине, в зависимости от положения хорды относительно центра окружности.

Хорды также могут быть использованы для измерения углов, образованных с центральными углами окружности. Такие углы называются углами, опирающимися на хорду.

В общем, понимание хорд и их свойств важно для различных областей математики, геометрии, физики и других научных дисциплин.

Для чего используют хорды в математике

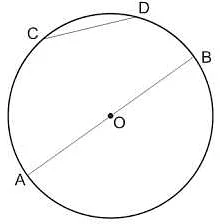
Одним из основных применений хорд является вычисление длины дуги. Зная длину хорды и радиус окружности, можно по формуле вычислить длину соответствующей дуги. Это полезно, например, при расчете длины пути, пройденного движущимся объектом, если известна его скорость и время движения.

Хорды также используются для нахождения расстояния между двумя точками на окружности. Если известны координаты этих точек, можно использовать формулу для вычисления длины хорды. Такой подход часто применяется в геометрии и тригонометрии при решении задач на построение треугольников и вычисление углов.

Кроме того, хорды используются для нахождения пересечений окружностей или окружности с прямыми. Если известны радиусы и центры окружностей, можно рассчитать координаты точек пересечения по формулам, использующим хорды.

Хорды также широко применяются в музыке. Например, в музыкальной гармонии хорды используются для создания аккордов и гармонического движения в музыкальных произведениях.

Таким образом, хорды являются важным понятием в математике и находят применение в различных областях, от геометрии до музыки.

Примеры использования хорд в геометрии

1. Построение центрального угла:
   • Выберите две точки на окружности и соедините их хордой.
   • Проведите радиусы от центра окружности к концам хорды.
   • Хорда разделит окружность на две дуги.
   • Центральный угол — это угол между этими дугами, с вершиной в центре окружности.
2. Нахождение длины хорды:
   • Известны радиус окружности и угол, натянутый хордой от центра.
   • Длина хорды может быть найдена по формуле: длина хорды = 2 * радиус * sin(угол/2).
3. Построение треугольника на основе хорды:
   • Выберите три точки на окружности и соедините их хордами.
   • Проведите радиусы от центра окружности к концам каждой хорды.
   • Получится треугольник, у которого каждая сторона является хордой.

Это лишь некоторые примеры использования хорд в геометрии. Хорды также могут быть использованы для нахождения длины дуги, определения точки пересечения хорд и других задач в геометрии.

Примеры использования хорд в анализе функций

Одним из примеров использования хорд в анализе функций является метод секущих. Этот метод позволяет приближенно найти корень функции. Для этого выбираются две точки на графике функции, соединяется хорда, и находится пересечение этой хорды с осью абсцисс. Затем процедура повторяется, пока не будет достигнута необходимая точность.

Еще одним примером использования хорд является приближенный метод Ньютона. В этом методе также выбираются две точки на графике функции и соединяется хорда. Затем находится точка пересечения хорды с осью абсцисс, и эта точка становится новым приближением корня функции. Процесс повторяется до достижения необходимой точности.

Использование хорд в анализе функций также может быть полезно для приближенного нахождения производной функции. Для этого выбираются две точки на графике функции, соединяется хорда, и находится угловой коэффициент этой хорды. Этот угловой коэффициент является приближенным значением производной функции в данной точке.

Пример использования хорд в анализе функцийМетод секущихПриближенный метод НьютонаНахождение приближенной производной

Описание	Поиск корня функции	Поиск корня функции	Нахождение производной функции
Выбор точек	Две точки на графике функции	Две точки на графике функции	Две точки на графике функции
Построение хорды	Соединение выбранных точек	Соединение выбранных точек	Соединение выбранных точек
Нахождение корня	Поиск пересечения хорды с осью абсцисс	Поиск пересечения хорды с осью абсцисс	Н/Д
Нахождение производной	Н/Д	Н/Д	Нахождение углового коэффициента хорды

Как найти длину хорды в математике

Если известны радиус окружности и угол, вписанный хордой, то длину хорды можно вычислить с помощью формулы:

L = 2r * sin(α/2)

где L – длина хорды, r – радиус окружности, α – угол, вписанный хордой.

Если известны координаты точек, через которые проходит хорда, то длину хорды можно вычислить с помощью координатных формул. Пусть (x1, y1) и (x2, y2) – координаты точек. Тогда длина хорды может быть найдена по формуле:

L = √((x2 — x1)^2 + (y2 — y1)^2)

где L – длина хорды, (x1, y1) и (x2, y2) – координаты точек.

Пример использования: пусть дана окружность с радиусом 5 и углом в 60 градусов, вписанным хордой. Для вычисления длины хорды используем формулу:

L = 2 * 5 * sin(60/2) = 2 * 5 * sin(30) = 2 * 5 * 0.5 = 5

Таким образом, длина хорды равна 5.

Методы вычисления длины хорды

В математике существует несколько способов вычисления длины хорды. Один из самых простых методов основан на использовании теоремы Пифагора.

Согласно теореме Пифагора, в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

Применительно к хорде можно представить себе равнобедренный треугольник, в котором хорда является основанием, а отрезок прямой, соединяющий середину хорды с вершиной треугольника, является высотой.

Таким образом, чтобы вычислить длину хорды, нужно сначала найти длину высоты этого треугольника, а затем, применив теорему Пифагора, найти длину хорды.

Если известна длина радиуса окружности, на которой лежит хорда, то можно использовать другой метод вычисления длины хорды. Согласно свойству хорд, проходящих через одну точку на окружности, отрезки хорд, радиусов и отрезков, соединяющих центр окружности с точками пересечения хорды с окружностью, образуют прямоугольный треугольник.

В этом случае можно использовать теорему Пифагора для вычисления длины хорды. Длина хорды будет равна дважды корню из разности квадрата длины радиуса и квадрата расстояния от центра окружности до точки пересечения хорды с окружностью.

Формулы для нахождения длины хорды

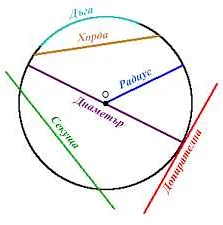
Если известны радиус окружности (R) и угол, под которым охвачена хорда (α), то длина хорды может быть вычислена по следующим формулам:

УсловияФормула для нахождения длины хорды (l)

Угол охваченной хорды измеряется в радианах	l = 2 * R * sin(α/2)
Угол охваченной хорды измеряется в градусах	l = 2 * R * sin(π * α/360)

Для подсчёта длины хорды также можно использовать теорему Пифагора. Если известны длины радиуса (R) и высоты (h), опущенной из центра окружности на хорду, то длина хорды (l) может быть найдена по формуле:

l = 2 * √(R^2 — h^2)

Эти формулы позволяют находить длину хорды на основе заданных параметров и использовать её в различных математических и инженерных расчетах.

Вопрос-ответ:

Что такое хорда в математике?

Хорда — это отрезок, соединяющий две точки на окружности.

Какие свойства имеет хорда?

Хорда имеет следующие свойства: длина хорды меньше диаметра окружности, хорда может быть равна диаметру окружности, хорда может быть параллельна диаметру окружности.

Какие примеры использования хорды в математике?

Хорда может использоваться для нахождения расстояния между двумя точками на окружности, для определения угла между хордой и радиусом, для решения задач на геометрическую прогрессию.

Как найти длину хорды, если известен радиус окружности и угол?

Длина хорды может быть найдена с помощью формулы: l = 2r*sin(α/2), где l — длина хорды, r — радиус окружности, α — угол, образованный хордой и радиусом.

В каких областях науки используется понятие хорды?

Понятие хорды активно используется в геометрии, физике, инженерии и компьютерной графике. Например, в архитектуре для построения круглых арок, в музыке для настройки струнных инструментов, в компьютерной графике для создания трехмерных моделей.