Что такое хорда кратко математика

Хорда в математике — это отрезок, соединяющий две точки на окружности. Узнайте, как рассчитать длину хорды и найти ее центральный угол с помощью простых математических формул и свойств окружности.

Хорда — это отрезок, соединяющий две точки на окружности. В математике хорда является одним из основных понятий, используемых при изучении геометрии окружности и тригонометрии. Хорда играет важную роль в различных математических и физических задачах, а также применяется в различных областях науки и техники.

Для полного определения хорды необходимо знать две ее характеристики: длину и расположение относительно окружности. Длина хорды определяется как расстояние между двумя точками, соединяющими ее концы. Расположение хорды относительно окружности определяется ее противоположными точками: точкой, которая лежит внутри окружности, и точкой, которая лежит вне окружности.

Примером хорды может служить струна на музыкальном инструменте. Длина струны соответствует длине хорды, а ее положение относительно грифа инструмента определяет расположение хорды относительно окружности. Хорда может быть как кратной, так и натуральной, в зависимости от соотношения длины хорды и радиуса окружности.

Определение хорды и ее свойства

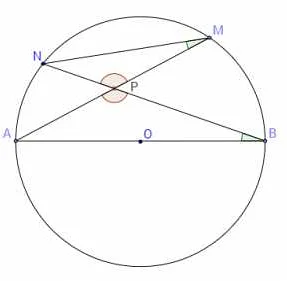
Свойства хорды:

1. Хорда всегда лежит внутри окружности и не может выходить за ее пределы.
2. Длина хорды может быть равна диаметру окружности или меньше его.
3. Всякая хорда, не являющаяся диаметром, делит окружность на две дуги. Эти дуги могут быть равными или неравными.
4. Если две хорды в окружности равны, то их соответствующие дуги равны.
5. Хорда, проходящая через центр окружности, называется диаметром. Диаметр является самой длинной хордой, так как проходит через центр и делит окружность на две равные дуги.

Хорды широко используются в геометрии и анализе для решения различных задач, связанных с окружностями.

Расстояние между точкой и хордой

Чтобы найти расстояние между точкой и хордой, можно использовать формулу:

Расстояние = 2 * радиус * sin(α/2)

где α – центральный угол, опирающийся на хорду, а радиус – расстояние от центра окружности до точки.

Например, пусть у нас есть окружность с радиусом 5 и хорда, на которой лежат точки А и В. Если мы хотим найти расстояние от точки С до хорды АВ, то для этого нам нужно знать центральный угол α, который опирается на хорду и проходит через точку С, а также радиус, который определяет расстояние от центра окружности до точки С. Подставив значения в формулу, мы можем найти искомое расстояние.

Расстояние между точкой и хордой является важным понятием в геометрии и находит применение в различных областях, таких как строительство, геодезия и физика.

Обратите внимание, что в данном контексте мы рассматриваем только расстояние от точки до хорды на окружности. Другие понятия расстояния, такие как расстояние между двумя точками в пространстве, могут иметь другие формулы и определения.

Середина хорды: определение и свойства

Свойства середины хорды:

• Середина хорды всегда лежит на самой хорде.
• Середина хорды также лежит на радиусе, перпендикулярном хорде.
• Если две хорды имеют общую середину, то эти хорды равны.

Середина хорды является важным понятием в геометрии, особенно в круговой геометрии. Она используется для решения различных задач, связанных с кругом, таких как построение касательных и нахождение длины хорды.

Центр хорды: понятие и примеры

Рассмотрим пример. Пусть дана окружность с центром O и радиусом r. Пусть AB — хорда этой окружности. Тогда точка M, являющаяся серединой хорды AB, будет центром этой хорды.

Для расчета координат центра хорды можно использовать формулу:

xM = (xA + xB) / 2

yM = (yA + yB) / 2

Например, если координаты точек A и B равны A(2, 4) и B(6, 8), то координаты центра хорды M будут:

xM = (2 + 6) / 2 = 4

yM = (4 + 8) / 2 = 6

Таким образом, центр хорды M будет иметь координаты (4, 6).

Касательная к окружности и хорда: взаимосвязь

Касательная и хорда взаимосвязаны в том смысле, что касательная может быть рассмотрена как специальный вид хорды. Касательная всегда является хордой, но не каждая хорда является касательной.

Одним из ключевых свойств касательной является то, что она перпендикулярна радиусу, проведенному в точке касания. Также, касательная к окружности будет иметь только одну точку пересечения с окружностью, в то время как хорда имеет две.

Важно отметить, что касательные и хорды используются в решении множества задач и проблем в геометрии и тригонометрии. Они являются основой для дальнейших изысканий и выводов, связанных с окружностями.

Взаимосвязь между касательной и хордой важна в понимании основных концепций и свойств окружностей в математике. Эти понятия позволяют решать различные задачи, связанные с окружностями, и проводить дальнейшие исследования в этой области.

Дуга хорды: определение и особенности

Основные особенности дуги хорды:

1. Дуга хорды всегда находится внутри окружности, и ее границы представляют собой хорду и соответствующую ей часть окружности.
2. Дуга хорды может быть равна длине хорды, если она составляет половину окружности.
3. Дуга хорды может быть меньше длины хорды, если она составляет меньшую часть окружности.
4. Дуга хорды может быть больше длины хорды, если она составляет большую часть окружности.
5. Дуга хорды может быть полуокружностью, если она соединяет диаметрально противоположные точки окружности.

Примеры:

Рассмотрим окружность с радиусом 5 и хордой, длина которой равна 8. Дуга хорды будет представлена частью окружности, ограниченной этой хордой. В данном случае длина дуги будет меньше длины хорды и составит, например, 6.

Если же хорда равна диаметру окружности, то дуга хорды будет являться полуокружностью, так как она соединяет диаметрально противоположные точки окружности.

Попарно пересекающиеся хорды: примеры и свойства

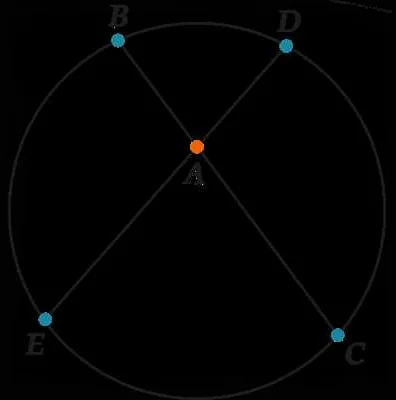
Примером попарно пересекающихся хорд может служить окружность, разделенная на равные секторы. Если провести хорды из центра окружности к точкам деления, то получатся попарно пересекающиеся хорды.

Свойства попарно пересекающихся хорд:

СвойствоОписание

Пересечение в одной точке	Любые две попарно пересекающиеся хорды пересекаются в одной точке, называемой точкой пересечения.
Равенство углов	Углы, образованные пересекающимися хордами, имеют равные меры.
Сумма дуг	Сумма дуг, ограниченных пересекающимися хордами, равна 360 градусов или полной окружности.

Таким образом, попарно пересекающиеся хорды обладают рядом интересных свойств и широко применяются в геометрии и теории чисел.

Параллельные хорды: характеристики и примеры

Основные характеристики параллельных хорд:

• Параллельные хорды имеют одинаковую длину. Это означает, что расстояние между двумя параллельными хордами и центром окружности одинаково.
• Любая хорда, параллельная касательной, является параллельной хордой. Если хорда параллельна касательной, то она также параллельна любой другой хорде, проходящей через точку касания.
• Если две хорды параллельны и пересекаются касательной, то углы, образованные этими хордами и касательной, равны или смежны.

Примеры параллельных хорд:

1. На рисунке видно, что хорда AB параллельна хорде CD, так как они расположены на одинаковом расстоянии от центра окружности.
2. В треугольнике DEF хорда DE параллельна хорде FG, так как обе хорды находятся на одинаковом расстоянии от центра окружности.

Таким образом, знание характеристик параллельных хорд позволяет более глубоко изучать геометрические фигуры и проводить различные выводы при решении задач.

Вопрос-ответ:

Как определить хорду?

Хорда — это отрезок, соединяющий две точки на окружности. Он является кратчайшим расстоянием между этими точками.

Какие свойства имеет хорда?

Хорда делит окружность на две дуги. Длина хорды равна произведению радиуса окружности на угол, заключенный между дугами, через которые она проходит.

Как можно использовать хорды в геометрии?

Хорды используются для нахождения различных характеристик окружности, таких как длина дуги, площадь сегмента окружности и площадь сектора окружности.

Можно ли построить хорду, которая является диаметром окружности?

Да, диаметр окружности также является хордой. В данном случае хорда будет проходить через центр окружности.

Можно ли хорду построить, если известны только ее длина и радиус окружности?

Да, если известна длина хорды и радиус окружности, то можно использовать теорему Пифагора для нахождения расстояния от центра окружности до хорды.

Видео по теме: