Что такое интерполяция в математике

Интерполяция в математике — это метод нахождения промежуточных значений функции на основе уже имеющихся точек. Узнайте, как работает интерполяция и как ее применяют в различных областях, таких как наука, инженерия и компьютерная графика.

Интерполяция — это метод математического анализа, который позволяет найти значения функции в точках, лежащих между известными значениями. Такой метод особенно полезен, когда нам известны только некоторые значения функции, но необходимо найти ее значения в других точках.

Обычно интерполяцию применяют, когда нужно аппроксимировать данные, то есть приближать функцию, проходящую через некоторые заданные точки. Для этого используются различные интерполяционные методы, такие как полиномиальная интерполяция, сплайн интерполяция, кубическая интерполяция и т.д.

Основной принцип интерполяции заключается в построении аппроксимирующей функции, проходящей через заданные точки. Для этого используются математические алгоритмы, которые учитывают связь между значениями функции и их положением на координатной плоскости.

Применение интерполяции широко распространено в различных областях науки и техники. Например, интерполяцию часто используют при построении графиков, при решении дифференциальных уравнений, в компьютерной графике и многих других областях.

Интерполяция является мощным инструментом математического анализа, который позволяет найти значения функции в точках, где их нет, но где они необходимы для решения задачи. Она позволяет аппроксимировать функцию и получать более точные результаты. Поэтому понимание основных принципов интерполяции является важным для всех, кто работает с математическими моделями и анализирует данные.

Интерполяция в математике: понятие и суть метода

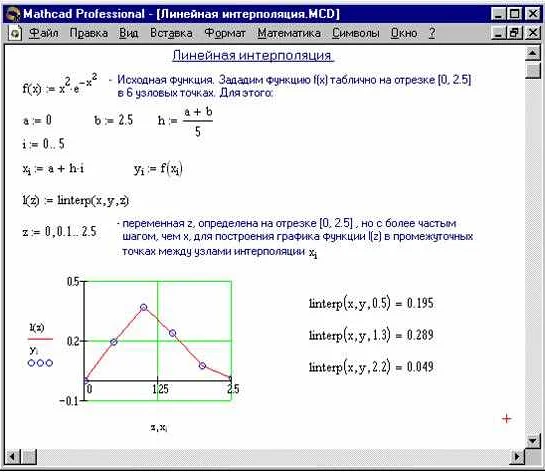
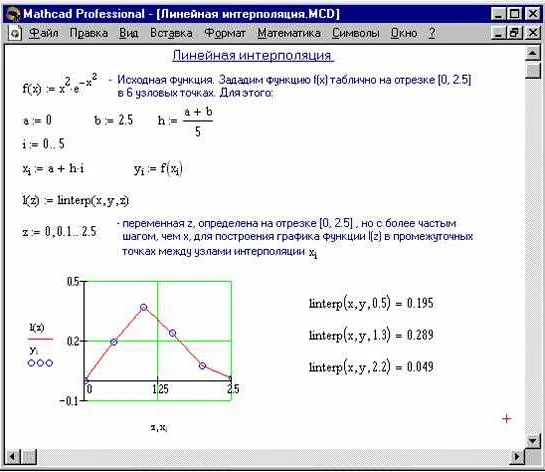
Суть метода интерполяции заключается в построении аппроксимирующей функции, которая проходит через заданные точки. Для этого используются различные математические методы, такие как метод наименьших квадратов или полиномиальная интерполяция. Результатом интерполяции является функция, которая приближает исходную функцию в заданных точках.

Интерполяция широко применяется в различных областях, таких как наука, инженерия, экономика и компьютерная графика. Она позволяет приближенно описывать сложные функции и строить графики по ограниченному набору данных. Благодаря интерполяции можно сделать предсказания и установить значения функции в промежуточных точках, что позволяет решать различные задачи, связанные с анализом и моделированием данных.

Точное определение интерполяции

Основной принцип интерполяции заключается в том, что мы стремимся найти функцию, которая проходит через известные точки данных и позволяет нам оценить значения функции в других точках. Для этого используются различные методы интерполяции, такие как полиномиальная интерполяция, сплайн-интерполяция и кусочно-линейная интерполяция.

Важно отметить, что интерполяция предполагает, что значения функции в известных точках являются точными. Однако в реальности это не всегда так. Поэтому при использовании интерполяции необходимо учитывать возможную погрешность и ограничения метода.

Интерполяция широко применяется в различных областях, таких как численное моделирование, анализ данных, графическое представление информации и т.д. Она позволяет заполнить пробелы в данных и предсказать значения функции в неизвестных точках, что делает ее мощным инструментом для анализа и прогнозирования.

Цель и принципы использования интерполяции

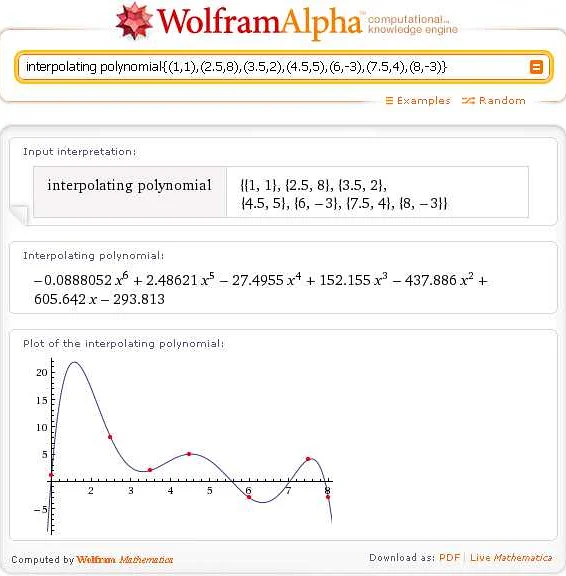
Принципы использования интерполяции включают следующее:

1. Искать наилучшую аппроксимацию: Интерполяционная функция должна наилучшим образом приближать данные в промежутках между заданными точками. На практике это означает минимизацию суммы квадратов отклонений между значениями функции и её аппроксимацией.
2. Выбирать подходящий метод интерполяции: Существует несколько методов интерполяции, включая полиномиальную интерполяцию, сплайн-интерполяцию и линейную интерполяцию. Выбор метода зависит от особенностей данных и требований к точности интерполяции.
3. Оценивать погрешность интерполяции: Погрешность интерполяции – это разница между реальными значениями функции и её интерполяцией. Важно оценивать погрешность, чтобы понимать точность и надёжность интерполяции.
4. Использовать интерполяцию с умом: Интерполяция может быть полезной в различных областях, таких как численные методы, графическое представление данных, моделирование и т.д. Однако необходимо осторожно использовать интерполяцию, поскольку она может привести к неверным результатам или искажению данных, особенно в случае недостаточного количества точек.

В целом, использование интерполяции позволяет нам работать с неполными или недостаточными данными, а также аппроксимировать функции на основе имеющихся точек. Это полезный инструмент, который находит широкое применение в математике, науке и инженерии.

Примеры применения интерполяции в реальной жизни

Ниже приведены некоторые примеры применения интерполяции в реальной жизни:

1. Геология: интерполяция используется для создания геологических моделей, предсказывающих состав и структуру земной коры. На основе измеренных значений на некоторых точках можно аппроксимировать значения для остальных точек, что помогает в изучении и обнаружении полезных ископаемых.
2. Метеорология: интерполяция применяется для создания прогнозов погоды. Данные о погоде собираются с помощью метеорологических станций, расположенных на определенных точках. Используя интерполяцию, можно предсказать погоду в промежуточных местах, где нет станций, основываясь на данных с ближайших станций.
3. Финансовая аналитика: интерполяция применяется для оценки финансовых инструментов. Например, если у вас есть данные о ценах акций на определенные даты, можно использовать интерполяцию, чтобы оценить цены на промежуточные даты и предсказать будущие тренды.
4. Картография: интерполяция используется для создания карт и моделей местности. На основе измерений высоты на некоторых точках можно аппроксимировать значения высоты для остальных точек, что помогает в создании детальных карт и моделей местности.
5. Медицина: интерполяция применяется для восстановления недостающих данных в медицинских исследованиях. Например, если у вас есть данные о здоровье пациентов на определенные моменты времени, можно использовать интерполяцию, чтобы заполнить пробелы и получить более полную картину их состояния.

Все эти примеры демонстрируют, как интерполяция помогает в анализе данных, предсказании результатов и заполнении пробелов в информации. Этот метод играет важную роль в различных отраслях и способствует более точному и полному анализу информации.

Методы интерполяции: различные подходы и алгоритмы

Одним из наиболее распространенных методов интерполяции является метод многочленов Лагранжа. В этом методе интерполяции полином строится таким образом, чтобы он проходил через все заданные точки данных. Однако этот метод может быть неэффективным при большом количестве точек, так как он может привести к появлению феномена Рунге.

Другим популярным методом интерполяции является метод сплайн-интерполяции. В этом методе функция разбивается на несколько отрезков, и на каждом отрезке используется полином низкой степени для аппроксимации данных. Такой подход позволяет более гибко аппроксимировать функцию и избежать проблемы Рунге.

Еще одним методом интерполяции является метод наименьших квадратов. В этом методе строится функция, которая минимизирует сумму квадратов разностей между значениями функции и их интерполяцией. Такой подход позволяет учесть возможные ошибки в исходных данных и получить наилучшую аппроксимацию функции.

Кроме вышеуказанных методов, существует также ряд других алгоритмов интерполяции, таких как метод ближайших соседей, кубическая интерполяция и экстраполяция. Каждый из них имеет свои преимущества и ограничения, и выбор метода зависит от конкретной задачи и доступных данных.

Разница между интерполяцией и экстраполяцией

Интерполяция используется для нахождения значения функции в промежуточных точках между известными значениями. Для этого используется предположение, что функция непрерывна и гладкая между заданными точками. Интерполяция позволяет «заполнить пробелы» между известными точками и получить более подробное представление функции.

Экстраполяция, с другой стороны, используется для предсказания значений функции вне диапазона заданных точек. Это означает, что экстраполяция основана на предположении, что функция имеет определенное поведение за пределами известных данных. Однако экстраполяция может быть менее точной, чем интерполяция, так как она основана на предположениях и может не учитывать особенности функции.

Разница между интерполяцией и экстраполяцией сводится к тому, что интерполяция используется для нахождения значений функции внутри диапазона известных точек, тогда как экстраполяция используется для предсказания значений функции за пределами этого диапазона. Оба метода полезны в различных ситуациях и могут быть использованы для аппроксимации данных в математике.

Основные формулы и уравнения, связанные с интерполяцией

• Формула Лагранжа: используется для построения интерполяционного многочлена, который проходит через заданные точки. Формула Лагранжа выглядит следующим образом:

$$

P(x) = \sum_{i=0}^{n} f(x_i)\prod_{j=0,j

eq i}^{n} \frac{x-x_j}{x_i-x_j}

$$

• Формула Ньютона (разделенные разности): эта формула также используется для построения интерполяционного многочлена. Она представляет собой разложение функции в виде суммы разделенных разностей. Формула Ньютона выглядит следующим образом:

$$

P(x) = f[x_0] + (x-x_0)f[x_0,x_1] + (x-x_0)(x-x_1)f[x_0,x_1,x_2] + \ldots + (x-x_0)(x-x_1)\ldots(x-x_{n-1})f[x_0,x_1,\ldots,x_n]

$$

• Формула Эрмита: используется для интерполяции функций, заданных значениями функции и ее производных. Формула Эрмита выглядит следующим образом:

$$

P(x) = f(x_0) + (x-x_0)f[x_0,x_0] + (x-x_0)^2f[x_0,x_0,x_1] + \ldots + (x-x_0)^nf[x_0,x_0,x_1,\ldots,x_n]

$$

Эти формулы и уравнения позволяют аппроксимировать функцию по заданным точкам и использовать полученный интерполяционный многочлен для вычисления значений функции в других точках.

Видео по теме:

Вопрос-ответ:

Что такое интерполяция?

Интерполяция — это метод математического анализа, который используется для построения функции или кривой, проходящей через заданный набор точек данных. Он позволяет оценить значения функции в промежуточных точках, основываясь на имеющихся данных.

Зачем нужна интерполяция?

Интерполяция часто используется для восстановления пропущенных данных или для уточнения значений функции между известными точками. Она также может быть полезна для аппроксимации сложной функции более простой моделью или для построения гладкой кривой, проходящей через заданные точки.

Какие методы интерполяции существуют?

Существует несколько методов интерполяции, включая линейную интерполяцию, полиномиальную интерполяцию, сплайн-интерполяцию и тригонометрическую интерполяцию. Каждый из этих методов имеет свои особенности и применяется в различных ситуациях в зависимости от требуемой точности и гладкости функции.

Как происходит процесс интерполяции?

Процесс интерполяции включает в себя выбор подходящего метода интерполяции, определение математической модели или функции, проходящей через заданные точки, и вычисление значений в промежуточных точках. Для этого может потребоваться решение системы уравнений или использование специальных алгоритмов, в зависимости от выбранного метода интерполяции.

Плюсы и минусы использования метода интерполяции

Интерполяция имеет свои преимущества и недостатки, которые следует учитывать при выборе и применении метода:

• Преимущества:
• 1. Универсальность: Метод интерполяции может быть применен к различным математическим функциям и наборам данных.
• 2. Гибкость: Интерполяция позволяет получать значения функции в промежуточных точках, что обеспечивает более точные результаты по сравнению с экстраполяцией.
• 3. Возможность аппроксимации: Метод интерполяции позволяет приближенно восстановить функцию по некоторому набору известных значений.
• 4. Простота и удобство: Интерполяционные методы имеют простую структуру и могут быть легко реализованы в различных программных средах.

• Недостатки:
• 1. Потеря точности: При интерполяции между известными значениями функции могут возникать погрешности, особенно в случае нелинейной зависимости.
• 2. Проблема выбора метода: Существует множество интерполяционных методов, и выбор наиболее подходящего может быть сложным.
• 3. Чувствительность к выбросам: Интерполяция может быть чувствительна к выбросам в данных, что может привести к искажению результатов.
• 4. Потребность в равномерно распределенных данных: Для получения точных результатов метод интерполяции требует наличия равномерно распределенных значений функции.

В целом, метод интерполяции является полезным инструментом в математике и науке, но его использование должно быть осознанным и с учетом его ограничений.

Интерполяция в компьютерной графике и программировании

Одним из наиболее распространенных методов интерполяции в компьютерной графике является линейная интерполяция. Он основан на предположении, что значение между двумя заданными точками изменяется равномерно. Этот метод используется для создания плавных переходов между двумя цветами или позициями объектов на экране.

Кроме линейной интерполяции, существуют и другие методы, такие как сплайновая интерполяция, которая используется для более сложных и гибких анимаций. Сплайн — это кривая, которая проходит через определенные точки и имеет гладкий и непрерывный характер.

Интерполяция также широко применяется в программировании для обработки данных. Например, при анализе временных рядов, интерполяция позволяет заполнить пропущенные значения между известными точками, чтобы получить более полное представление данных. Это особенно полезно при работе с большими наборами данных или при анализе сигналов.

В заключение, интерполяция в компьютерной графике и программировании играет важную роль в создании плавных и реалистичных изображений, а также в обработке и анализе данных. Различные методы интерполяции позволяют получить гладкие и непрерывные переходы между точками или значениями и значительно улучшить визуальное и аналитическое представление информации.