Что такое эллипс в математике

Эллипс — это геометрическая фигура в математике, представляющая собой замкнутую кривую, которая образуется при пересечении плоскости и конуса под определенным углом. В данной статье вы узнаете о свойствах эллипса, его уравнении и применении в различных областях науки и техники.

Эллипс — это одна из основных фигур в математике, которая имеет множество интересных свойств и применений. Он встречается не только в геометрии, но и в других областях, таких как физика, астрономия и технические науки.

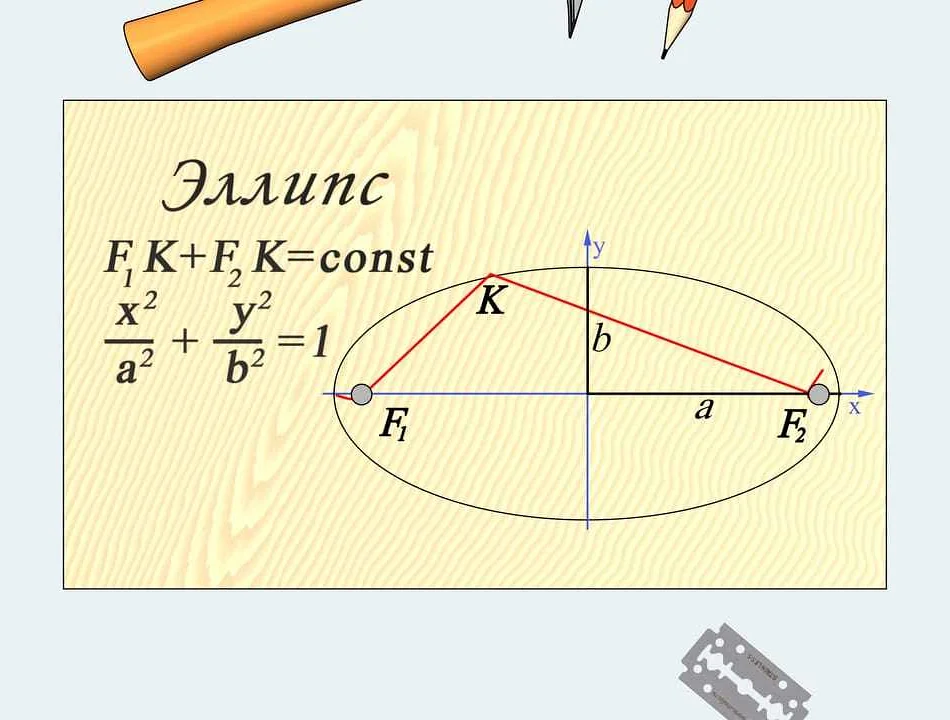
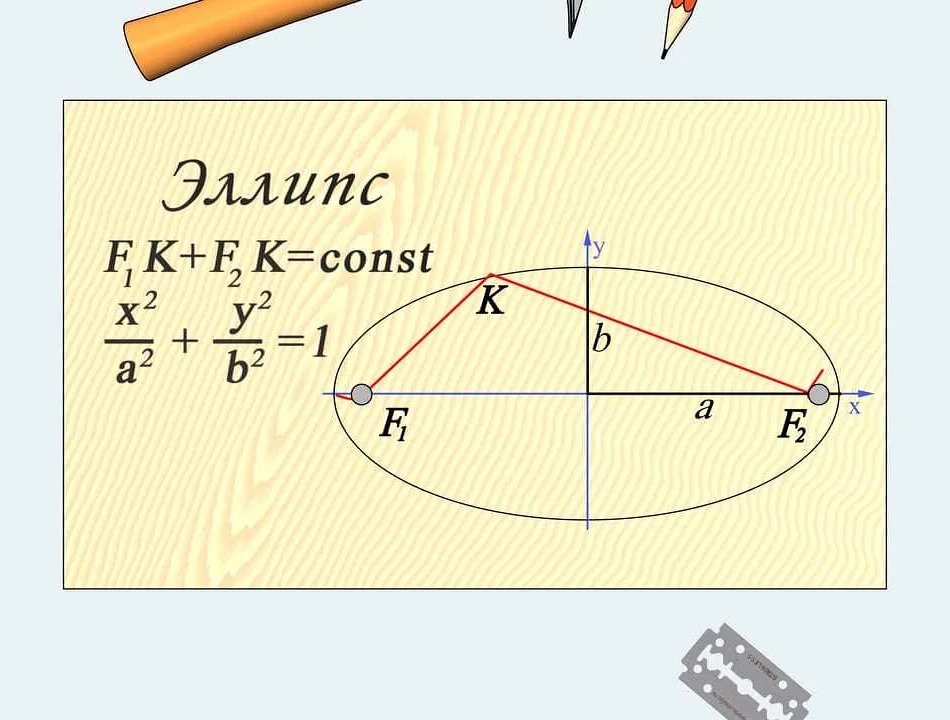
Эллипс можно определить как геометрическое место точек на плоскости, для которых сумма расстояний до двух фиксированных точек, называемых фокусами, постоянна. Эти две фокусы находятся на одной горизонтальной линии, но могут быть расположены на разных расстояниях от центра эллипса.

Основные свойства эллипса включают его форму, фокусы,оси и радиусы. Эллипс симметричен относительно своих осей и имеет две оси — большую и малую. Большая ось является самой длинной линией, проходящей через центр эллипса и соединяющей два его наиболее удаленных точки, называемых вершинами. Малая ось — это линия, перпендикулярная большой оси и проходящая через центр эллипса.

Примеры применения эллипса можно найти в различных областях. Например, эллипсы используются при построении спутниковых орбит, расчете времени движения планет и гравитационном взаимодействии между небесными телами. Кроме того, эллипсы могут быть использованы для моделирования движения электрона в атоме, в конструировании камеры сверхвысокого разрешения и даже при создании изделий на промышленных предприятиях.

Что такое эллипс в математике

Фокусы эллипса находятся на одной прямой, называемой главной осью эллипса. Половина длины главной оси называется большой полуосью, обозначается как a, и определяет размер эллипса в направлении главной оси. Половина длины побочной оси называется малой полуосью, обозначается как b, и определяет размер эллипса в направлении, перпендикулярном главной оси.

Эллипс имеет следующие свойства:

1. Длина главной оси равна удвоенному значению большой полуоси, то есть a = 2a.
2. Фокусное расстояние равно 2a.
3. Сумма расстояний от любой точки на эллипсе до двух фокусов равна 2a.
4. Эллипс симметричен относительно своей главной оси и обладает центральной симметрией относительно центра.
5. Эллипс является плоской кривой второго порядка.

Примерами эллипсов могут служить форма орбит планет вокруг Солнца, форма спутниковых орбит и некоторые геометрические фигуры в природе.

Определение эллипса в математике

Эллипс имеет следующие основные свойства:

Фокусы	Два точечных фокуса, обозначаемых F1 и F2, которые находятся на большой оси эллипса и служат для определения его формы и размеров.
Большая и малая оси	Большая ось (2a) является отрезком, соединяющим два фокуса, а малая ось (2b) — отрезком, перпендикулярным к большой оси и проходящим через центр эллипса.
Центр	Точка пересечения большой и малой осей, обозначаемая как (h, k), является центром эллипса.
Эксцентриситет	Эксцентриситет эллипса обозначается как e и определяется как отношение расстояния между фокусами к длине большой оси: e = c/a, где c — расстояние между фокусами, a — половина длины большой оси.

Примеры эллипсов в реальной жизни включают форму орбит планет вокруг Солнца, форму спортивного стадиона и форму яйца.

Свойства эллипса

1. Диаметры: эллипс имеет два диаметра — большой и малый. Большой диаметр проходит через центр эллипса и соединяет две самые удаленные точки на его окружности. Малый диаметр, наоборот, проходит через центр, но соединяет две самые близкие точки на окружности.
2. Фокусы: эллипс имеет две фокусные точки, которые находятся по обе стороны от центра. Сумма расстояний от каждой точки эллипса до фокусов всегда одинакова и равна длине большого диаметра.
3. Оси: эллипс имеет две оси — большую и малую. Большая ось параллельна большому диаметру и проходит через центр эллипса. Малая ось параллельна малому диаметру и также проходит через центр.
4. Эксцентриситет: эксцентриситет эллипса — это мера его «приплюснутости». Он равен отношению расстояния между фокусами к длине большого диаметра. Эксцентриситет эллипса всегда находится в диапазоне от 0 до 1, где 0 означает, что эллипс является окружностью, а 1 означает, что эллипс очень «приплюснутый».

Свойства эллипса позволяют нам лучше понять его форму и характеристики. Они также используются при решении задач и построении графиков.

Фокусы эллипса

Сумма расстояний от любой точки эллипса до двух его фокусов всегда равна длине большой оси эллипса. Это свойство называется фокусным свойством эллипса и помогает определить его форму и размеры.

Фокусы эллипса также помогают определить его эксцентриситет — меру «сплюснутости» фигуры. Эксцентриситет эллипса можно найти как отношение расстояния между фокусами к длине большой оси эллипса.

Фокусы эллипса имеют важное геометрическое значение и используются не только в математике, но и в различных областях, таких как физика, оптика и астрономия.

Эксцентриситет эллипса

Эксцентриситет обычно обозначается символом e и является числом от 0 до 1. Чем ближе значение эксцентриситета к 0, тем более круговой будет эллипс. Когда эксцентриситет равен 0, получаем окружность. А чем ближе значение эксцентриситета к 1, тем более вытянутой и «тонкой» будет эллипс.

Эксцентриситет эллипса также связан с его формой и ориентацией. Чем больше эксцентриситет, тем более вытянутой будет форма эллипса, а ориентация будет ближе к вертикальной, если эксцентриситет больше 1, или к горизонтальной, если эксцентриситет меньше 1.

Наличие эксцентриситета позволяет нам определить фокусы эллипса и другие важные характеристики этой геометрической фигуры.

Например, пусть у нас есть эллипс с большой полуосью a и малой полуосью b. Тогда эксцентриситет можно выразить формулой:

e = √(1 — (b^2/a^2))

Формула эллипса

Формула эллипса в общем виде имеет следующий вид:

Горизонтальный радиусВертикальный радиус

a

b

Таким образом, эллипс можно записать как:

x2/a2 + y2/b2 = 1

где x и y — координаты точек на эллипсе, а a и b — полуоси эллипса.

Также можно выразить эллипс в параметрической форме с помощью параметров t, где:

x = acos(t)

y = bsin(t)

где t изменяется от 0 до 2π, обеспечивая полный оборот вокруг эллипса.

Примеры эллипсов в природе

2. Форма глаза: Форма глаза человека, а также многих животных, также может быть приближена эллипсом. Эллиптическая форма глаза позволяет лучше собирать свет и обеспечивает более ясное зрение.

3. Форма орехов: Многие орехи, такие как грецкий орех или миндаль, имеют форму эллипса. Это связано с оптимальной структурой, которая обеспечивает максимальную прочность и эффективность распределения нагрузки.

4. Форма капли воды: Капли воды, падающие на поверхность, часто принимают форму эллипса. Это связано с поверхностным натяжением воды, которое приводит к минимизации ее поверхности и формированию эллиптической формы.

5. Форма падающего метеорита: Падающие метеориты часто имеют эллиптическую форму. Это связано с их траекторией движения в атмосфере Земли, где они подвергаются силам атмосферного сопротивления.

6. Форма листьев и цветов: Некоторые листья и цветы имеют эллиптическую форму. Это особенно видно у некоторых сортов лилий и кувшинок, где лепестки образуют эллиптическую форму.

7. Форма вулканических кратеров: Вулканические кратеры на поверхности Земли могут иметь форму эллипса. Это связано с их образованием в результате взрывов и выбросов материала изнутри земной коры.

Примеры эллипсов в технике

Эллипсы широко применяются в различных областях техники. Ниже приведены несколько примеров, где эллипсы играют важную роль:

1. Оптика: В линзах и зеркалах эллипсы используются для фокусировки света. Форма эллипса позволяет сфокусировать световые лучи в одной точке, что активно применяется в оптических системах.

2. Радиоинженерия: В антеннах эллипсы используются для усиления и диаграммы направленности сигнала. Форма эллипса позволяет получить узкую диаграмму направленности, что особенно важно для дальнейшей передачи и приема сигналов.

3. Телекоммуникации: В системах связи эллипсы используются для модуляции и демодуляции сигнала. Форма эллипса позволяет эффективно передавать данные, так как сигналы могут быть представлены в виде эллиптических волн.

4. Механика: В механических системах эллипсы применяются в траекториях движения объектов. Например, в плоском движении планеты вокруг Солнца траектория описывает эллипс.

5. Электроника: В электронных схемах эллипсы используются для формирования и фильтрации сигналов. Например, эллиптические фильтры часто применяются в радиотехнике для подавления нежелательных частот.

Это лишь некоторые примеры использования эллипсов в технике. Этот геометрический объект имеет широкий спектр применения и продолжает находить свое применение в различных областях науки и техники.

Видео по теме:

Что такое эллипс в математике?

Эллипс — это геометрическая фигура, которая представляет собой замкнутую кривую, образованную точками, сумма расстояний от которых до двух фокусов постоянна. Он имеет форму овала и является одной из конических секций.

Как можно определить эллипс математически?

Эллипс можно определить математически с помощью уравнения в декартовой системе координат. Уравнение эллипса имеет форму (x/a)^2 + (y/b)^2 = 1, где a и b — полуоси эллипса. Это уравнение описывает все точки, которые лежат на эллипсе.