Что такое комплексные числа в математике

Комплексные числа в математике — это числа, состоящие из действительной и мнимой частей. Они играют важную роль в алгебре, физике и других областях науки. Узнайте, как работать с комплексными числами и зачем они нужны.

Комплексные числа — это расширение обычных (действительных) чисел на мнимую ось. В комплексных числах каждое число представляется в виде суммы действительной и мнимой части. Мнимая единица обозначается символом i и определяется как квадратный корень из -1.

Использование комплексных чисел широко распространено в математике, физике и инженерии. Они играют важную роль в решении уравнений, где требуется учесть взаимодействие действительных и мнимых компонентов. Комплексные числа позволяют решать уравнения, которые невозможно решить с использованием только действительных чисел.

Применение комплексных чисел находится во многих областях математики. Они используются в алгебре, геометрии, теории вероятностей и других разделах. Комплексные числа также широко применяются в электротехнике, где они используются для анализа и проектирования электрических цепей и сигналов.

Комплексные числа имеют множество интересных свойств, таких как алгебраические операции, аргумент и модуль числа. Они позволяют решать уравнения, которые невозможно решить с использованием только действительных чисел. Комплексные числа также играют важную роль в теории функций, где они позволяют определить понятия такие как голоморфность и аналитичность.

В заключение, комплексные числа являются мощным инструментом, который нашел применение во многих областях математики и наук. Они позволяют решать сложные уравнения и анализировать различные явления. Понимание комплексных чисел является важным компонентом математической грамотности и может быть полезно в решении реальных проблем.

Что такое комплексные числа?

Комплексные числа широко применяются в математике, физике и инженерии. Они позволяют решать уравнения, которые не имеют решений в обычных действительных числах. Кроме того, комплексные числа используются в теории вероятностей, сигнальной обработке, электронике и других областях.

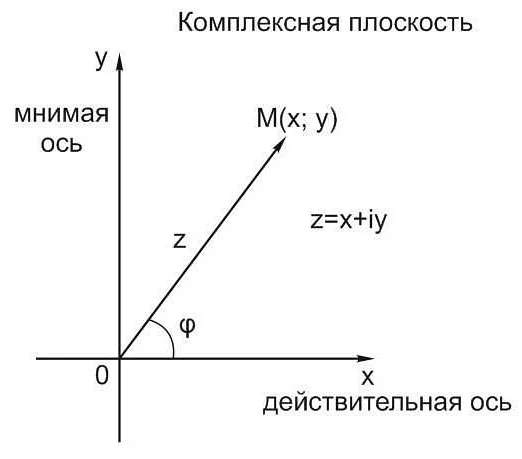
Комплексные числа могут быть представлены в виде точек на комплексной плоскости, где действительная часть является координатой по оси X, а мнимая часть — координатой по оси Y. Сложение и умножение комплексных чисел имеют геометрическую интерпретацию на этой плоскости.

ОперацияЗначение

Сложение	(a + bi) + (c + di) = (a + c) + (b + d)i
Умножение	(a + bi)(c + di) = (ac — bd) + (ad + bc)i

Как они представлены в математике?

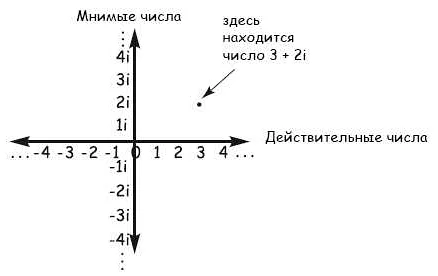
Обозначение комплексного числа в общем виде выглядит следующим образом: z = a + bi, где a — вещественная часть, а bi — мнимая часть, а i — мнимая единица.

Вещественная часть комплексного числа представляет собой действительное число, а мнимая часть представляет собой число, умноженное на мнимую единицу i.

Комплексные числа можно представить не только в алгебраической форме, но и в тригонометрической форме, экспоненциальной форме и других формах.

Комплексные числа используются в различных областях математики, таких как анализ, теория вероятностей, электротехника и другие. Они позволяют решать задачи, которые не могут быть решены с использованием только вещественных чисел.

Основы комплексных чисел

Комплексные числа представляют собой числа, которые состоят из двух частей: вещественной и мнимой. Вещественная часть комплексного числа обозначается как Re, а мнимая часть обозначается как Im.

Мнимая единица i является основой комплексных чисел и определяется как квадратный корень из -1. Таким образом, любое комплексное число может быть представлено в виде z = a + bi, где a — вещественная часть, а b — мнимая часть.

Комплексные числа можно складывать, вычитать, умножать и делить так же, как и обычные числа. При сложении или вычитании комплексных чисел, вещественные части и мнимые части суммируются или вычитаются отдельно. При умножении комплексных чисел, используется правило распределения, а при делении — правило умножения на сопряженное число.

Комплексные числа широко применяются в математике и физике. Они используются, например, для решения уравнений, моделирования физических явлений и анализа колебательных процессов. Также комплексные числа имеют важное значение в электротехнике и теории сигналов.

Декартова форма записи

В математике комплексные числа обычно записываются в декартовой форме, которая представляет собой пару вещественной и мнимой частей числа. Данная форма записи имеет вид:

z = a + bi,

где a — вещественная часть, а bi — мнимая часть комплексного числа.

В этой форме комплексные числа представляются в виде точек в декартовой плоскости, где вещественная часть числа является координатой по оси абсцисс, а мнимая часть — координатой по оси ординат. Такая геометрическая интерпретация комплексных чисел позволяет удобно выполнять операции с ними, такие как сложение, вычитание, умножение и деление.

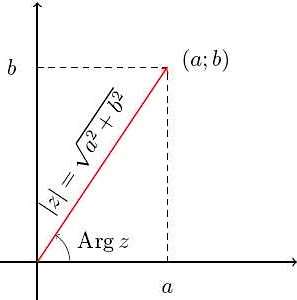
Декартова форма записи комплексных чисел также позволяет представить число в виде модуля и аргумента. Модуль комплексного числа определяет его расстояние от начала координат до точки, представляющей число, и вычисляется по формуле:

|z| = √(a^2 + b^2).

Аргумент комплексного числа определяет угол между положительным направлением оси абсцисс и лучом, соединяющим начало координат и точку, представляющую число. Аргумент вычисляется с помощью тригонометрической функции:

arg(z) = arctan(b/a).

Декартова форма записи комплексных чисел является одним из наиболее удобных способов работы с ними и широко используется в различных областях математики и физики.

Тригонометрическая форма записи

Комплексные числа могут быть записаны в тригонометрической форме. Эта форма представляет комплексное число в виде модуля и аргумента.

Модуль комплексного числа выражает его расстояние от начала координат до точки, которая соответствует этому числу на комплексной плоскости. Он вычисляется по формуле:

|z|

=

√(Re(z)2 + Im(z)2)

где Re(z) — действительная часть комплексного числа, Im(z) — мнимая часть комплексного числа.

Аргумент комплексного числа определяет угол между положительным направлением оси действительных чисел и лучом, исходящим из начала координат и заканчивающемся в точке, которая соответствует этому числу на комплексной плоскости. Аргумент вычисляется по формуле:

arg(z)

=

arctg(Im(z)/Re(z))

где arctg — арктангенс.

Таким образом, тригонометрическая форма записи комплексного числа имеет вид:

z

=

|z| ∠ arg(z)

где |z| — модуль комплексного числа, arg(z) — аргумент комплексного числа.

Тригонометрическая форма записи позволяет более наглядно представить комплексные числа и удобно работать с ними в различных математических операциях.

Применение комплексных чисел

Комплексные числа широко применяются в различных областях математики и физики. Они позволяют решать уравнения, которые не имеют решений в вещественных числах, а также описывать и анализировать явления, которые не могут быть объяснены с помощью вещественных чисел.

Одной из основных областей применения комплексных чисел является электротехника. В комплексной форме можно описывать переменные электрические величины, такие как напряжение и ток. Комплексные числа позволяют проводить алгебраические операции с этими величинами и решать уравнения, связанные с электрическими цепями.

Комплексные числа также находят применение в теории вероятностей и статистике, например, при описании случайных процессов. Они используются для моделирования и анализа сложных систем, таких как финансовые рынки или трафик в сетях связи.

В геометрии комплексные числа позволяют представлять точки на плоскости с помощью пар чисел (действительной и мнимой части). Они используются в комплексном анализе, где помогают исследовать функции, аналитически продолжать их и решать уравнения.

Кроме того, комплексные числа имеют важное значение в теории дифференциальных уравнений, где они используются для нахождения общих решений и анализа поведения систем дифференциальных уравнений.

Область примененияПримеры

Электротехника	Описание переменных электрических величин
Теория вероятностей и статистика	Моделирование случайных процессов
Геометрия и комплексный анализ	Представление точек на плоскости и исследование функций
Теория дифференциальных уравнений	Нахождение общих решений и анализ систем уравнений

В решении уравнений

Комплексные числа широко используются в математике для решения уравнений. Они позволяют найти корни уравнений, которые не имеют решений в обычных действительных числах.

Если уравнение имеет комплексные корни, то они обычно представляются в виде a + bi, где a и b — действительные числа, а i — мнимая единица, которая определяется как квадратный корень из -1.

Для нахождения комплексных корней уравнения можно использовать формулу Кардано-Виета, которая выражает корни через коэффициенты уравнения. Также можно использовать графический метод, основанный на построении комплексной плоскости и определении точек пересечения графиков уравнения и осей координат.

Комплексные числа также применяются при решении систем уравнений, когда одно из уравнений имеет комплексные корни. В этом случае решение системы можно найти, используя методы линейной алгебры и комплексных чисел.

В электротехнике

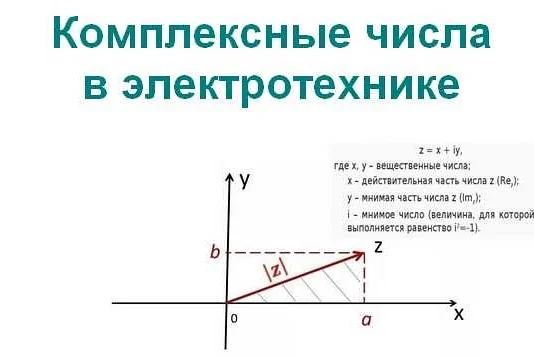
Комплексные числа широко применяются в электротехнике для решения различных задач. Взаимоотношения между напряжением и током в электрических цепях могут быть представлены комплексными числами. Использование комплексных чисел позволяет упростить расчеты и анализ электрических цепей.

Комплексное сопротивление является одним из важных понятий в электротехнике. Оно представляет собой комбинацию активного (сопротивления) и реактивного (индуктивности или ёмкости) элементов цепи. Комплексное сопротивление определяет взаимодействие сигналов в цепи, анализ которого осуществляется с помощью комплексных чисел.

Также комплексные числа используются для описания и анализа электромагнитных полей. Электромагнитные поля могут быть представлены с помощью комплексных векторов, где вещественная часть соответствует действительной составляющей поля, а мнимая часть — мнимой составляющей.

В области электротехники комплексные числа также применяются для решения уравнений и задач, связанных с переменным током, фазами и сдвигами фаз, анализа электрических схем и др.

В целом, использование комплексных чисел в электротехнике позволяет более удобно и эффективно описывать и анализировать электрические явления и процессы.

Видео по теме:

Вопрос-ответ:

Зачем нужны комплексные числа?

Комплексные числа используются для решения математических задач, которые связаны с проблемами, не решаемыми обычными действительными числами. Они широко применяются в различных областях, таких как физика, инженерия, электроника и теория вероятностей.

Какие операции можно выполнять с комплексными числами?

С комплексными числами можно выполнять все основные арифметические операции, такие как сложение, вычитание, умножение и деление. Кроме того, комплексные числа поддерживают возведение в степень, извлечение корня и тригонометрические операции.

Как записываются комплексные числа?

Комплексные числа записываются в виде a + bi, где a и b — это действительные числа, а i — мнимая единица, которая определяется как i^2 = -1. Действительная часть комплексного числа обычно обозначается Re(z), а мнимая часть — Im(z).

Какие примеры применения комплексных чисел в математике можно привести?

Комплексные числа находят применение в различных областях математики. Например, они используются в теории функций комплексного переменного, где комплексные переменные помогают описывать сложные функции и решать уравнения. Кроме того, комплексные числа используются в теории вероятностей для моделирования случайных процессов.

Сложение и умножение комплексных чисел

Сложение и умножение комплексных чисел осуществляются в соответствии с определенными правилами.

Для сложения двух комплексных чисел a + bi и c + di мы просто складываем их действительные и мнимые части отдельно:

(a + bi) + (c + di) = (a + c) + (b + d)i

То есть, сумма двух комплексных чисел равна сумме их действительных и мнимых частей.

Умножение комплексных чисел производится по формуле:

(a + bi) * (c + di) = (ac — bd) + (ad + bc)i

Таким образом, чтобы умножить два комплексных числа, мы перемножаем их действительные части, вычитаем произведение мнимых частей и прибавляем произведение действительной и мнимой частей.

Сложение и умножение комплексных чисел имеют свойства коммутативности и ассоциативности, что позволяет выполнять операции с ними в любом порядке.

Сложение

Комплексные числа можно складывать, аналогично вещественным числам. Сложение комплексных чисел происходит по правилу: сумма двух комплексных чисел равна сумме их действительных и мнимых частей.

Пусть даны два комплексных числа: z1 = a + bi и z2 = c + di, где a, b, c и d — вещественные числа, а i — мнимая единица. Тогда сумма этих чисел будет равна: zsum = (a + c) + (b + d)i.

Например, сложим комплексные числа z1 = 2 + 3i и z2 = -1 + 4i:

zsum = (2 + (-1)) + (3 + 4)i = 1 + 7i.

Таким образом, сложение комплексных чисел позволяет нам суммировать их действительные и мнимые части, расширяя возможности математических операций и решение различных задач.