Что такое компоненты в математике 3

Компоненты в математике 3 — это элементы, составляющие сложные объекты и позволяющие их анализировать и решать задачи. Узнайте, какие компоненты используются в математике 3 и как они связаны между собой.

Компоненты являются одним из важных понятий в математике и широко используются в различных областях. Они представляют собой отдельные части или элементы, из которых состоит исследуемый объект или система. В математике компоненты могут быть различных типов — числами, векторами, матрицами и т.д.

Компоненты часто используются для описания различных свойств и характеристик объекта или системы. Например, вектор может быть представлен в виде компонентов, которые указывают его направление и длину. Компоненты матрицы могут представлять собой отдельные элементы этой матрицы или подматрицы.

Примерами компонентов в математике могут служить координаты точки в пространстве, составляющие её положение относительно начала координат, компоненты вектора силы, определяющие его направление и величину, или элементы матрицы, представляющие собой скаляры или другие матрицы.

Важно отметить, что компоненты являются отдельными частями объекта или системы и могут рассматриваться и анализироваться независимо от остальных компонентов. Изучение компонентов позволяет получить более глубокое понимание структуры и свойств объекта или системы в целом.

В заключение, компоненты являются ключевым понятием в математике и позволяют разбить сложные объекты или системы на более простые и понятные составляющие. Изучение компонентов помогает получить более полное и глубокое представление о структуре и свойствах объекта или системы.

Определение компоненты в математике

Компоненты могут быть различными по своей природе. Например, вектор в трехмерном пространстве состоит из трех компонентов – координат по осям x, y и z. При работе с матрицами можно выделить элементы, которые являются отдельными компонентами. Также можно говорить о компонентах в функциях, графах, уравнениях и других математических объектах.

Знание компонентов и их взаимосвязи позволяет лучше понять и изучить математические объекты, а также применять их в решении конкретных задач. Разбивая сложные структуры на более простые компоненты, удобно анализировать и моделировать различные математические явления и процессы.

Виды компонент в математике

В математике компоненты могут быть различного вида и служить разным целям.

1. Векторы: Векторы — это один из важнейших видов компонент в математике. Векторы представляют собой направленные отрезки, которые имеют длину и направление. Они широко используются в физике, геометрии и других областях математики.

2. Матрицы: Матрицы — это таблицы чисел, расположенных в виде прямоугольной сетки. Они используются для представления и решения систем линейных уравнений, а также для хранения и обработки данных в компьютерных программах.

3. Функции: Функции — это специальный вид компонент, который связывает каждый элемент одного множества с элементом другого множества. Функции широко используются для описания зависимостей между величинами и решения различных задач.

4. Графы: Графы — это набор вершин и ребер, которые связывают вершины друг с другом. Графы используются для моделирования сложных сетей и взаимосвязей между объектами, таких как социальные сети, транспортные системы и т.д.

5. Дроби: Дроби — это числа, представленные в виде отношения двух целых чисел. Дроби используются для представления нецелых значений и использования более точных вычислений.

Это лишь некоторые виды компонент в математике. Каждый вид имеет свои особенности и применения в разных областях математики и других науках.

Компоненты в алгебре

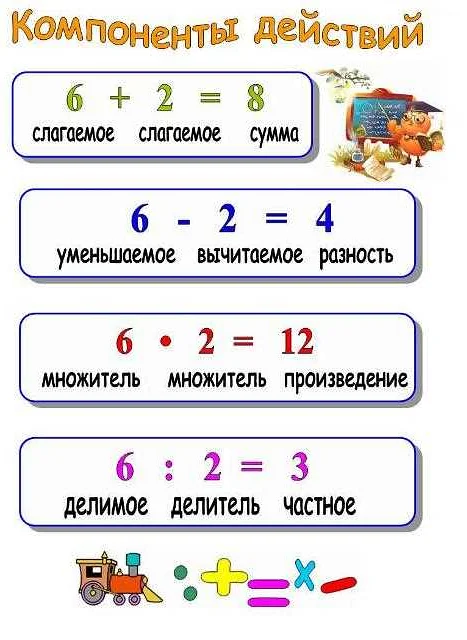
В алгебре компонентами называются отдельные части алгебраических объектов, таких как векторы, матрицы или многочлены. Компоненты позволяют разложить сложные объекты на более простые части и представить их в виде суммы или произведения этих частей.

Например, вектор в трехмерном пространстве может быть представлен в виде суммы трех компонент: компонент по оси X, компонент по оси Y и компонент по оси Z. Аналогично, матрица может быть представлена в виде суммы компонент, каждая из которых является отдельным элементом матрицы.

Компоненты играют важную роль в алгебре, так как они позволяют анализировать и решать сложные математические задачи путем разложения их на более простые части. Они также используются для определения операций над алгебраическими объектами и описания их свойств.

Компоненты в геометрии

Одним из примеров компонентов в геометрии являются отрезки. Отрезок — это часть прямой между двумя точками. Отрезок может быть компонентом более сложных фигур, например, треугольника или многоугольника. Изучение отрезков позволяет получить более точные и подробные характеристики геометрических фигур.

Другим примером компонентов в геометрии являются углы. Угол — это область плоскости, образованная двумя лучами, исходящими из одной точки. Углы могут быть компонентами более сложных фигур, таких как многоугольники или окружности. Изучение углов позволяет определить форму и свойства геометрических фигур.

Компоненты в геометрии являются важными элементами для анализа и понимания различных геометрических фигур. Они позволяют более детально изучить форму и свойства фигур, а также упрощают решение геометрических задач.

Компоненты в теории вероятности

В теории вероятности компоненты могут представлять собой как отдельные события, так и части случайной величины. Например, в случае подбрасывания монеты, компонентами могут быть выпадение орла или решки.

Компоненты могут быть независимыми или зависимыми друг от друга. Независимые компоненты встречаются, когда вероятность одного компонента не зависит от других компонентов. Зависимые компоненты, наоборот, имеют взаимосвязь между собой и вероятность одного компонента зависит от других.

Примером компонентов в теории вероятности может служить бросок двух кубиков. В данном случае компонентами будут выпадение определенных чисел на каждом кубике. Например, выпадение 3 на первом кубике и 5 на втором кубике.

Примеры компонент в математике

ПримерОписание

x + 3	Компоненты этого выражения — переменная x и число 3. Сумма этих компонент равна выражению x + 3.
2a — b	Компоненты этого выражения — переменные a и b, а также числа 2 и -1. Разность этих компонент равна выражению 2a — b.
4x^2 + 7y — z	Компоненты этого выражения — переменные x, y и z, а также числа 4 и 7. Сумма и разность этих компонент равны выражению 4x^2 + 7y — z.

В каждом примере компоненты могут быть разных типов — переменные, числа, операторы. Их комбинация и взаимодействие определяют значение выражения или уравнения.

Компоненты в линейной алгебре

В линейной алгебре компоненты представляют собой отдельные части вектора или матрицы. Компоненты могут быть числами или переменными и служат для описания различных параметров или характеристик объектов. Часто компоненты вектора или матрицы могут иметь физический смысл и использоваться для решения различных задач.

Например, вектор в трехмерном пространстве можно представить с помощью трех компонент: x, y и z. Каждая компонента будет отвечать за координату по соответствующей оси. Таким образом, вектор будет иметь вид (x, y, z), где каждая компонента — это отдельная числовая переменная.

Матрица также состоит из компонент, которые располагаются в виде таблицы. Каждая компонента матрицы может быть числом или переменной. Компоненты матрицы могут использоваться для описания различных характеристик объектов или для решения систем уравнений.

Таким образом, компоненты в линейной алгебре играют важную роль в описании и решении различных математических задач, позволяя представить объекты в виде чисел или переменных и использовать их в дальнейших вычислениях.

Компоненты в арифметике

Однако, в более сложных выражениях, компонентами могут быть не только числа, но и переменные или другие математические выражения. Например, в выражении x + y, x и y являются компонентами, причем они представляют переменные, а не конкретные числа.

Компоненты в арифметике могут принимать разные формы и выполнять различные функции в зависимости от контекста. Например, в выражении 2 * (3 + 4), числа 2, 3 и 4 являются компонентами, но выполняют разные роли. Число 2 является множителем, числа 3 и 4 являются слагаемыми.

Также, компонентами могут быть различные математические операции, такие как умножение, деление или возведение в степень. Например, в выражении 2 * 3 + 4, числа 2, 3 и 4 являются компонентами, но 2 и 3 являются множителями, а 4 — слагаемым.

Итак, компоненты в арифметике представляют числа, переменные или математические операции, которые участвуют в вычислении. Они могут принимать разные формы и выполнять различные функции в зависимости от контекста.

Вопрос-ответ:

Что такое компоненты в математике?

Компоненты в математике — это отдельные части или элементы, из которых состоит математический объект или система. Они могут быть числами, переменными, функциями или другими математическими объектами, которые могут быть выделены и рассмотрены независимо от остальных элементов системы.

Какие примеры компонентов в математике?

Примерами компонентов в математике могут быть числа, переменные, операторы, функции и математические объекты, такие как векторы, матрицы или графы. Например, в уравнении x + y = 2, компонентами являются переменные x и y, а также число 2.

В каких областях математики используются компоненты?

Компоненты используются во многих областях математики, включая алгебру, геометрию, анализ, теорию вероятностей и дискретную математику. Они являются основными строительными блоками для построения математических моделей и решения различных математических задач.

Как компоненты влияют на решение математических задач?

Компоненты играют важную роль в решении математических задач, так как позволяют анализировать и рассматривать отдельные элементы системы независимо от остальных. Это позволяет более эффективно и точно решать задачи, разбивая их на более простые подзадачи и применяя соответствующие методы и операции к компонентам.

Каким образом компоненты помогают в понимании математических концепций?

Компоненты помогают в понимании математических концепций, так как позволяют выделить и изучить отдельные элементы системы. Это позволяет лучше понять, как они взаимодействуют друг с другом и как они влияют на результат. Анализ компонентов помогает построить более глубокое и полное представление о математической теме или концепции.

Видео по теме: