Что такое компонент в математике
Содержимое
- 1 Что такое компонент в математике
- 1.1 Определение компонента в математике
- 1.2 Примеры компонентов в математике
- 1.3 Как определить компонент в математике
- 1.4 Свойства компонента в математике
- 1.5 Графическое представление компонента в математике
- 1.6 Классификация компонентов в математике
- 1.7 Применение компонентов в математике
- 1.8 Вопрос-ответ:
- 1.9 Видео по теме:
Компонент в математике — это отдельная часть или элемент, который входит в состав более крупной структуры или системы. Этот термин часто используется в различных областях математики, включая геометрию, алгебру и теорию графов. Компоненты могут быть уникальными и иметь свои собственные характеристики, но в то же время они также могут быть взаимозависимыми и взаимосвязанными с другими компонентами. Понимание компонентов является важным аспектом в математике, и оно помогает увидеть общую структуру и связи между различными элементами в различных математических моделях и системах.
Математика — это наука, изучающая строгие законы и отношения между числами, фигурами и объектами. Одним из важных понятий в математике является компонент. Компонент — это отдельная часть или элемент, составляющий какую-либо систему или объект.
В математике компоненты часто используются для разделения сложных объектов на более простые и понятные части. Это помогает упростить анализ и решение задач. Компоненты могут быть представлены числами, символами, формулами или графическими элементами.
Примером компонента может служить уравнение, которое состоит из нескольких частей, таких как числа, переменные и операции. Каждая часть уравнения является компонентом, который можно анализировать и использовать для решения задачи.
Например, уравнение x + 2 = 5 имеет три компонента: переменная x, число 2 и число 5. Анализируя каждый компонент по отдельности, мы можем найти значение переменной x, которая равна 3.
В математике компоненты также могут использоваться для описания геометрических фигур. Например, треугольник может быть разделен на три компонента: стороны, углы и высоты. Анализируя каждый компонент, мы можем определить свойства и характеристики треугольника.
Таким образом, компоненты играют важную роль в математике, помогая разбить сложные объекты на более простые части и анализировать их отдельно. Изучение компонентов помогает понять и решить математические задачи, а также строить сложные модели и системы.
Определение компонента в математике
В математике компонентом называют отдельную часть или составную часть объекта или структуры данных. Компоненты могут быть физическими объектами, числами, переменными или любыми другими элементами, которые составляют целое.
Компоненты позволяют разбить сложные объекты или структуры на более простые составляющие, что упрощает их анализ и понимание. Например, в графах компонентами являются отдельные вершины и ребра, которые связывают их.
Примерами компонентов могут служить отдельные числа в математике, такие как 1, 2, 3 и т.д., или отдельные переменные, такие как x, y, z. В контексте графов, компонентами могут быть отдельные вершины или связанные между собой вершины.
Изучение компонентов позволяет анализировать и понимать сложные системы или структуры, разбирая их на более простые составляющие. Это помогает решать различные математические задачи и применять их в различных областях науки, техники и экономики.
Примеры компонентов в математике

В математике компонентами могут быть различные элементы, которые входят в состав более сложных структур или систем.
Например, в векторной алгебре компонентами вектора являются его координаты. Если вектор задан в трехмерном пространстве, то его компонентами будут три числа, отражающие его положение по осям x, y, z.
В теории множеств компонентами могут быть отдельные элементы множества. Например, если рассматривается множество натуральных чисел, то его компонентами будут отдельные числа: 1, 2, 3 и так далее.
В матричной алгебре компонентами матрицы являются ее элементы. Если матрица задана размером 3×3, то ее компонентами будут 9 чисел, расположенных в ячейках матрицы.
Таким образом, компоненты в математике представляют собой отдельные элементы или числа, которые образуют более сложные структуры или системы.
Как определить компонент в математике
Например, в алгебре компонент может быть подмножеством множества или частью алгебраической структуры. В графовой теории компонентом может быть связная часть графа, которая не имеет ребер с остальными частями графа. В теории вероятностей компонент может быть случайной величиной или событием.
Определение компонента может иметь разные применения и интерпретации в разных областях математики, поэтому важно учитывать контекст и конкретную задачу, когда речь идет о компонентах в математике.
Свойства компонента в математике

Свойство 1: Составная структура. Компонент является составной частью системы или объекта. Он не может существовать отдельно от этой системы и вносит свой вклад в общую структуру. Например, в математической функции компонентами являются аргументы и значения, которые они принимают.
Свойство 2: Взаимодействие. Компоненты взаимодействуют друг с другом внутри системы или объекта. Они могут передавать информацию, влиять на друг друга или выполнять совместные действия. Например, в графе компоненты могут быть вершинами, а ребра между ними — взаимодействием.
Свойство 3: Уникальность. Каждый компонент обладает своими уникальными характеристиками, которые отличают его от других компонентов. Эти характеристики могут включать в себя имя, значение, тип или другие параметры, которые определяют его функциональность и роль в системе. Например, в матрице каждый элемент является уникальным компонентом.
Свойство 4: Изменяемость. Компоненты могут изменяться во времени или в зависимости от внешних условий. Они могут приобретать новые значения, менять свое состояние или функциональность. Например, в динамическом графе вершины и ребра могут добавляться или удаляться в процессе работы системы.
Свойство 5: Взаимозаменяемость. Некоторые компоненты могут быть взаимозаменяемыми, то есть выполнять одну и ту же функцию или роль в системе. Это означает, что при замене одного компонента другим, система будет продолжать работать без изменений. Например, в уравнении различные числа могут быть взаимозаменяемыми компонентами при условии, что они удовлетворяют одному и тому же уравнению.
Эти свойства помогают понять и анализировать компоненты в математике, определять их роль и взаимодействие в системе, а также применять математические методы и операции для работы с ними.
Графическое представление компонента в математике

В математике компонент представляет собой одну из составных частей объекта или системы, которые могут быть выделены и рассмотрены отдельно. Графическое представление компонента позволяет наглядно представить его структуру и связи с другими частями.
Одним из способов графического представления компонента является использование диаграмм. Диаграмма компонентов позволяет отобразить компоненты и их связи в виде прямоугольников, которые представляют отдельные части системы. Компоненты могут быть связаны друг с другом стрелками, которые указывают на направление связи и их тип.
Другим способом графического представления компонента является использование графов. Граф компонентов представляет собой совокупность вершин и ребер, где вершины представляют компоненты, а ребра — связи между компонентами. Графы позволяют наглядно представить структуру и связи компонентов, а также анализировать их свойства, например, определять наличие циклов или пути между компонентами.
Графическое представление компонента позволяет упростить визуальное восприятие системы и помогает проводить анализ и проектирование. Оно является важным инструментом в различных областях математики, таких как теория графов, системное анализ и др.
Классификация компонентов в математике
В зависимости от природы и свойств компоненты могут быть классифицированы следующим образом:
КлассификацияОписаниеПримеры
| Числовые компоненты | Компоненты, которые представляют числа | 1, 2, 3, 4, 5 |
| Геометрические компоненты | Компоненты, которые описывают геометрические фигуры и их свойства | окружность, треугольник, прямая |
| Алгебраические компоненты | Компоненты, которые связаны с алгеброй и алгебраическими операциями | переменная, уравнение, многочлен |
| Функциональные компоненты | Компоненты, которые представляют функции и их свойства | синус, косинус, логарифм |
| Матричные компоненты | Компоненты, связанные с матрицами и их операциями | матрица, определитель, транспонирование |
Классификация компонентов помогает математикам систематизировать знания и облегчает понимание математической теории и ее приложений.
Применение компонентов в математике

Применение компонентов в математике может быть иллюстрировано на примере алгебры. В алгебре компоненты могут быть переменными, числами, функциями и операциями. Например, выражение «3x + 2y» состоит из трех компонентов: числа 3, переменной x и переменной y. Каждый из этих компонентов представляет собой отдельную часть выражения, которую можно анализировать и решать отдельно.
В математических выражениях компоненты могут быть объединены различными операциями, такими как сложение, вычитание, умножение и деление. Например, выражение «3x + 2y» объединяет компоненты «3x» и «2y» операцией сложения. Компоненты также могут быть объединены в более сложные структуры, такие как функции или уравнения.
Применение компонентов в математике позволяет упростить сложные выражения и уравнения, разбивая их на более простые части. Это упрощает процесс анализа и решения математических задач, так как каждая часть выражения может быть рассмотрена и решена отдельно. Кроме того, компоненты позволяют строить более сложные структуры и выражения, что расширяет возможности математического анализа и решения различных задач.
ПримерВыражениеКомпоненты
| 1 | x + y | x, y |
| 2 | 2x — 3y | 2x, -3y |
| 3 | (x + y)(x — y) | x + y, x — y |
В приведенной таблице показаны примеры выражений и их компоненты. Выражение «x + y» состоит из двух компонентов: переменной x и переменной y. Выражение «2x — 3y» состоит из двух компонентов: умножение числа 2 на переменную x и умножение числа -3 на переменную y. Выражение «(x + y)(x — y)» состоит из двух компонентов: суммы переменных x и y и разности переменных x и y.
Таким образом, применение компонентов в математике является важным инструментом, который помогает упростить сложные выражения и решить математические задачи. Они позволяют разбивать выражения на более простые части и объединять их в более сложные структуры, что делает математический анализ и решение более эффективными и удобными.
Вопрос-ответ:
Что такое компонент в математике?
Компонент в математике — это часть или элемент, составляющий более сложный объект. В математических структурах, таких как графы или векторы, компоненты являются частями, из которых состоят эти объекты.
Какие примеры компонентов можно привести?
Примеры компонентов в математике включают вершины и ребра в графе, координаты векторов, числа в множестве и элементы матрицы. В каждом случае компоненты представляют собой отдельные части, которые вместе образуют более сложный объект.
Как компоненты связаны с составными объектами в математике?
Компоненты являются составными частями более сложных математических объектов. Например, в графе компонентами являются вершины и ребра, а вектор состоит из координатных компонентов. Компоненты могут быть использованы для анализа и понимания структуры и свойств этих объектов.
Как важно понимание компонентов в математике?
Понимание компонентов в математике важно для анализа и решения различных задач. Знание компонентов позволяет нам лучше понять структуру и свойства объектов, таких как графы, векторы, матрицы и другие. Оно также помогает нам разрабатывать эффективные алгоритмы и модели для работы с этими объектами.
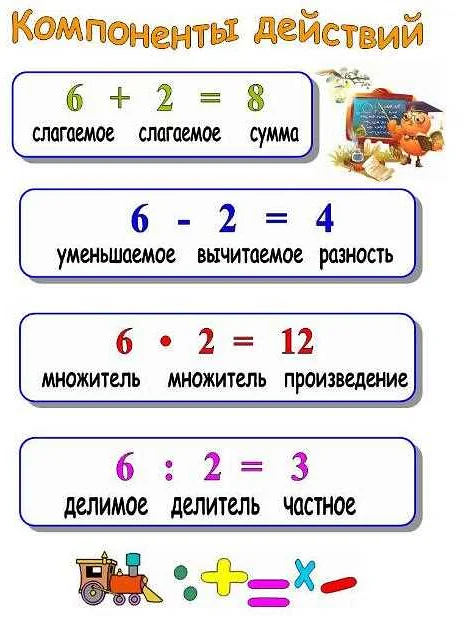
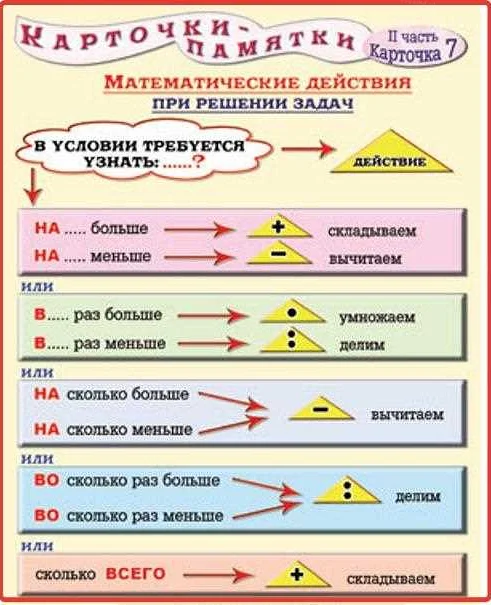
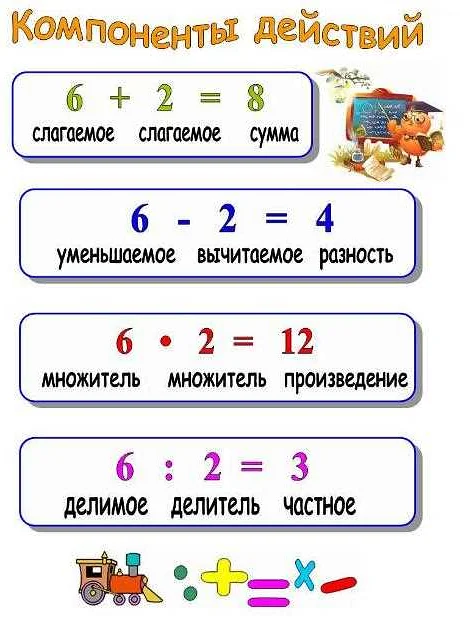
Компонент в математике — это основная составляющая, из которых состоит объект или система. Он играет важную роль в анализе и позволяет разбить сложные структуры на более простые элементы для более глубокого понимания. Например, в графах компонентами являются связные подграфы, которые не имеют связей с остальными узлами. Это позволяет изучать структуру графа внутри каждого компонента отдельно. Компоненты также широко используются в алгебре, где они представляют отдельные части сложных алгебраических объектов, таких как векторные пространства или группы. Компоненты помогают упростить аналитические вычисления и сделать математические структуры более доступными для изучения и применения.
Статья очень понятно объясняет, что такое компоненты в математике. Я давно интересуюсь этой наукой, но всегда было сложно разобраться в таких понятиях. Статья даёт четкое определение компонента и приводит примеры, что очень помогает в понимании. Она хорошо структурирована и легка в чтении. Теперь я точно знаю, что компонент — это связная часть графа или связного пространства. Примеры с геометрическими фигурами и сетями дополняют объяснение и помогают усвоить материал. Статья была для меня очень полезной и понятной. Теперь я смогу применить новые знания в своих исследованиях и проблемах. Большое спасибо автору!
Отличная статья! Я всегда был немного запутан в определении компонента в математике, но теперь мне все стало ясно. Теперь я понимаю, что компонент — это связная часть графа или связное множество вершин. Понятно, что компоненты могут быть различного размера и формы, но главное, что они объединяют вершины, между которыми есть путь. Очень наглядный пример, который приведен в статье про компоненты связности в сетях — это социальные сети. Я сам активный пользователь социальных сетей, и теперь я понимаю, что все мои друзья и знакомые находятся в одной компоненте связности. Интересно, что если бы я не был «дружен» с кем-то из них, то мы бы находились в разных компонентах и наша связь была бы прервана. Теперь я понимаю, что компоненты связности играют очень важную роль в анализе сетей и современных технологиях. Спасибо за информацию!
Компонент в математике — это, безусловно, самое основное понятие, которое нужно знать для понимания многих математических концепций. В простых словах, это часть или элемент, из которых состоит математический объект. Компоненты могут быть различных видов — числа, переменные, операции и т. д. Одним из примеров компонента может быть числовая переменная «x» в алгебре. Она является основным элементом, с которым мы работаем при решении уравнений. Еще одним примером может быть операция сложения. В выражении «2 + 3», числа 2 и 3 являются компонентами, а операция сложения — связующим элементом между ними. Понимание компонентов помогает нам разбираться в сложных математических концепциях и решать сложные задачи. Без этого понятия мы не смогли бы строить сложные формулы, решать уравнения и доказывать теоремы. Поэтому, понимание компонентов — это ключевая составляющая успешного изучения математики.