Что такое координация в математике 5 класс
Содержимое
- 1 Что такое координация в математике 5 класс
- 1.1 Что такое координация в математике 5 класс
- 1.2 Определение понятия «координация»
- 1.3 Важность изучения координации в математике
- 1.4 Примеры задач на координацию
- 1.5 Методы решения задач на координацию
- 1.6 Теория координатной плоскости
- 1.7 Координаты точек на координатной плоскости
- 1.8 Видео по теме:
- 1.9 Вопрос-ответ:
- 1.9.0.1 Как определить, что две фигуры на плоскости координированы?
- 1.9.0.2 Как можно использовать координацию в решении математических задач?
- 1.9.0.3 Какие инструменты используются для работы с координацией в математике?
- 1.9.0.4 Какие примеры задач можно решить, используя координацию?
- 1.9.0.5 Какова роль координации в развитии математического мышления?
- 1.10 Графики функций и координация
- 1.11 Задачи на координацию в жизни
Координация в математике для 5 класса — это навык определения и использования координатной плоскости, графиков и алгебраических выражений. Узнайте, какие концепции и навыки связаны с координацией и как они применяются в учебной программе для пятого класса.
Координация – это одно из важнейших понятий в математике, которое изучается уже на уроках начальной школы. Она позволяет определить положение точки или фигуры на координатной плоскости и решать множество задач различной сложности.
Координатная плоскость – это двумерное пространство, на котором оси Ox и Oy пересекаются в точке O. Каждая точка на плоскости имеет свои координаты – абсциссу (откладывается по оси Ox) и ординату (откладывается по оси Oy). Таким образом, координаты точки – это числа, которые определяют ее положение относительно начала координат.
Решение задач по координации требует умения работать с числами, проводить простейшие вычисления, а также анализировать и интерпретировать графики различных функций. Например, для нахождения расстояния между двумя точками на плоскости или для определения координат середины отрезка необходимо применить формулы и правила координации.
Координация в математике 5 класса – это первый шаг в изучении алгебры и геометрии. Она позволяет ученикам развивать логическое мышление, абстрактное мышление, воображение и способность анализировать информацию. Задачи по координации требуют от учеников применять различные математические знания и умения, а также развивают навыки работы с геометрическими фигурами и понимание алгебраических выражений.
Что такое координация в математике 5 класс
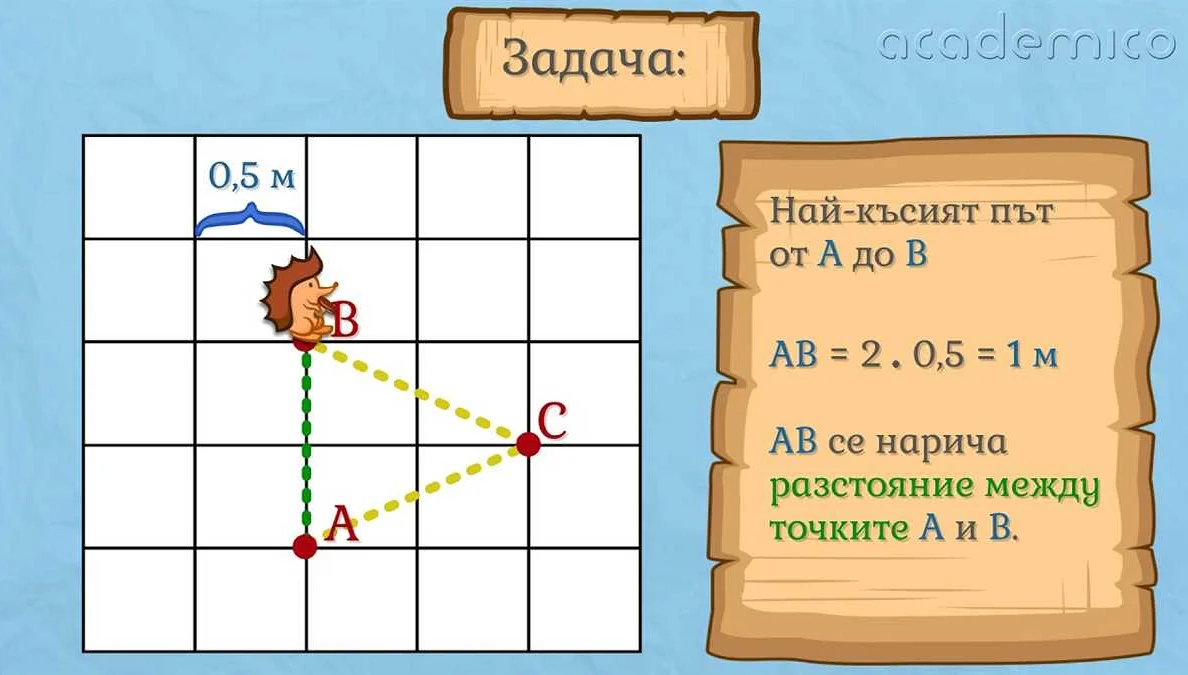
Одним из основных элементов координации является координатная плоскость, которая представляет собой двумерную систему координат, состоящую из двух взаимно перпендикулярных прямых — осей координат. Горизонтальная ось называется осью абсцисс или осью X, а вертикальная ось — осью ординат или осью Y.
Чтобы определить положение точки на координатной плоскости, нужно знать ее координаты. Координаты точки состоят из двух чисел: абсциссы (X-координата) и ординаты (Y-координата). Координаты точки записываются в виде упорядоченной пары чисел (X, Y).
Для работы с координатами используются различные величины и понятия, такие как расстояние между точками, симметрия относительно осей, направление движения и т.д. Координация позволяет решать разнообразные задачи, например, находить расстояние между точками, находить середину отрезка, находить точку пересечения двух графиков функций и многое другое.
В 5 классе ученики начинают изучать основы координации и практические навыки работы с координатами. Они учатся строить координатные оси, откладывать числа на оси, находить координаты точек на плоскости и строить графики функций. Знание координации является важным фундаментом для дальнейшего изучения математики и решения различных задач.
Определение понятия «координация»
Координаты точки в системе координат определяются ее расстоянием от начала координат по каждой из осей. Горизонтальная ось (ось X) представляет собой горизонтальную линию, на которой точки имеют координаты, увеличивающиеся слева направо. Вертикальная ось (ось Y) представляет собой вертикальную линию, на которой точки имеют координаты, увеличивающиеся снизу вверх.
Координаты точки в системе координат записываются в виде упорядоченной пары чисел (x, y), где x — координата по горизонтальной оси (ось X), а y — координата по вертикальной оси (ось Y). Например, точка с координатами (2, 5) находится на расстоянии 2 единицы от начала координат по оси X и на расстоянии 5 единиц от начала координат по оси Y.
Координация в математике используется для решения различных задач, таких как нахождение расстояния между двумя точками, определение площади фигуры или построение графика функции. Понимание координации помогает ученикам развивать навыки анализа и пространственного мышления, а также применять их на практике.
Важность изучения координации в математике
Изучение координации помогает ученикам развить навыки анализа и интерпретации данных, а также способность решать проблемы и принимать решения на основе математических моделей. Оно также способствует развитию логического мышления и абстрактного мышления учеников.
Знание координатной системы и умение работать с координатами точек позволяет ученикам изучать различные геометрические фигуры, решать уравнения и неравенства, а также решать задачи на расстояния и направления.
Изучение координации также имеет практическую ценность. Оно находит применение в различных областях науки и техники, таких как физика, экономика, география и компьютерная графика. Навыки работы с координатами являются основой для изучения более сложных математических концепций и методов, таких как векторы, матрицы и дифференциальное исчисление.
В целом, изучение координации в математике позволяет ученикам развить важные навыки и концепции, которые применяются не только в математике, но и в различных других областях знания и практики. Это помогает ученикам не только понять математические концепции, но и применять их в реальной жизни.
Примеры задач на координацию
1. Найдите координаты середины отрезка с концами в точках (-2, 3) и (4, -1).
2. Определите координаты точки, которая лежит на отрезке с концами в точках (1, 5) и (-3, 2) и делит его в отношении 2:3.
3. Найдите координаты точки пересечения прямых, заданных уравнениями y = 2x — 1 и y = -x + 3.
4. Найдите координаты вершины параболы, заданной уравнением y = x^2 — 4x + 3.
5. Определите, лежат ли точки A(2, 4), B(-1, 3) и C(0, 6) на одной прямой.
6. Определите, является ли треугольник с вершинами A(1, 2), B(3, 7) и C(-2, 5) прямоугольным.
7. Найдите длину отрезка, соединяющего точки (-3, -5) и (2, 1).
8. Определите, лежит ли точка P(-2, 3) внутри окружности с центром в точке O(1, -2) и радиусом 4.
9. Дан треугольник с вершинами A(1, 3), B(4, -2) и C(-2, -1). Найдите его площадь.
10. Найдите координаты точки, симметричной точке (-3, 5) относительно оси ординат.
Методы решения задач на координацию

При решении задач на координацию в математике 5 класса можно использовать различные методы. Некоторые из них включают:
| 1. Метод графического представления Этот метод основан на построении графиков и использовании координатной плоскости. Для решения задачи можно построить соответствующий график и анализировать его характеристики. |
| 2. Метод алгебраических выражений Этот метод предполагает использование алгебраических выражений и уравнений для решения задач на координацию. Задачу можно сформулировать в виде уравнения и решить его с помощью известных методов алгебры. |
| 3. Метод пространственного мышления Этот метод предполагает представление задачи в трехмерном пространстве. С помощью трехмерной координатной системы можно визуализировать задачу и найти ее решение. |
Выбор метода решения задачи на координацию зависит от ее конкретных условий и требований. Важно уметь адаптировать методы в зависимости от поставленной задачи и использовать различные инструменты математического анализа для достижения решения.
Теория координатной плоскости

Ось абсцисс разделяет плоскость на две полуплоскости – правую и левую, а ось ординат – на две полуплоскости – верхнюю и нижнюю. Пересечение этих осей образует точку, которая называется началом координат (точка O).
Координаты точек на плоскости задаются парой чисел (x, y), где x – это абсцисса точки, а y – ордината точки. Абсцисса указывает расстояние от начала координат до точки по горизонтальной оси, а ордината – по вертикальной оси. Таким образом, каждая точка на плоскости имеет свои уникальные координаты.
Координаты точек на координатной плоскости
Каждая точка на координатной плоскости имеет свои координаты, которые обозначаются парой чисел (x, y). Координата x указывает положение точки по горизонтали на оси абсцисс, а координата y — по вертикали на оси ординат.
Для определения координаты точки на координатной плоскости сначала находим пересечение прямых, соответствующих значениям x и y. Затем, считая от начала координат, определяем значение x и значение y.
Например, точка A имеет координаты (2, 3). Это означает, что она находится на 2 единицы правее начала координат по оси абсцисс и на 3 единицы выше начала координат по оси ординат.
Точки на координатной плоскости можно также задавать с помощью таблицы. В таблице указываются значения x и y для каждой точки. В первом столбце указываются значения x, а во втором столбце — значения y.
xy
| 0 | 0 |
| 1 | 2 |
| 2 | 3 |
| 3 | 1 |
Таким образом, точка с координатами (1, 2) находится на 1 единицу правее начала координат и на 2 единицы выше начала координат.
Видео по теме:
Вопрос-ответ:
Как определить, что две фигуры на плоскости координированы?
Две фигуры на плоскости считаются координированными, если их вершины совпадают. Для этого необходимо сравнить координаты всех вершин фигур: если они совпадают, то фигуры координированы.
Как можно использовать координацию в решении математических задач?
Координация в математике позволяет упростить решение задач, связанных с геометрией и алгеброй. Зная координаты точек, можно вычислить расстояние между ними, найти середину отрезка, определить эквивалентность геометрических фигур и многое другое.
Какие инструменты используются для работы с координацией в математике?
Для работы с координацией в математике используются координатная плоскость, система координат, а также геометрические инструменты, такие как линейка и циркуль.
Какие примеры задач можно решить, используя координацию?
Примеры задач, которые можно решить, используя координацию, включают вычисление расстояния между двумя точками, нахождение середины отрезка, определение эквивалентности двух геометрических фигур и многое другое.
Какова роль координации в развитии математического мышления?
Координация играет важную роль в развитии математического мышления, так как позволяет абстрагироваться от конкретных фигур и работать с абстрактными математическими моделями. Это помогает развивать логическое и пространственное мышление, а также улучшать навыки анализа и решения задач.
Графики функций и координация
В математике координация играет важную роль при изучении графиков функций. График функции представляет собой графическое представление зависимости между переменными в функции. Для построения графика функции необходимо знать координаты точек, которые определяют эту зависимость.
Координаты точек на плоскости обычно записываются в виде пары чисел (x, y), где x — это значение переменной x, а y — значение функции, соответствующее этому значению x. Например, для функции y = 2x + 3, координаты точки (1, 5) означают, что при x = 1, y равно 5.
Для построения графика функции нужно найти несколько точек, принадлежащих графику, и соединить их линиями. Чтобы найти координаты точек на графике функции, можно использовать таблицу значений, где для каждого значения переменной x находится соответствующее значение y. Эти значения затем можно отобразить на плоскости и соединить линиями, чтобы получить график функции.
Координация в математике позволяет визуально представить зависимости между переменными и понять, как изменение одной переменной влияет на другую. Изучение графиков функций помогает развивать навыки анализа и решения задач, а также понимание основ математики.
Задачи на координацию в жизни
Важно развивать свою координацию, чтобы быть гибкими и ловкими, а также предотвращать возможные травмы. Поэтому существует множество задач и упражнений, которые помогают улучшить координацию в разных сферах жизни.
Примеры задач на координацию в жизни:
ЗадачаОписание
| Хождение по линии | Передвигаться по прямой линии, не отклоняясь. |
| Балансирование на одной ноге | Стоять на одной ноге без поддержки в течение определенного времени. |
| Ловля мяча | Поймать мяч, бросаемый с разной скоростью и направлением. |
| Координация рук и глаз | Выполнять задачи, требующие точности и согласованности движений рук и глаз. |
| Танцы и хореография | Выполнять сложные танцевальные движения в ритме музыки. |
Это лишь небольшая часть примеров задач на координацию в жизни. Развивая свою координацию, мы становимся более гибкими, ловкими и успешными в различных сферах деятельности.
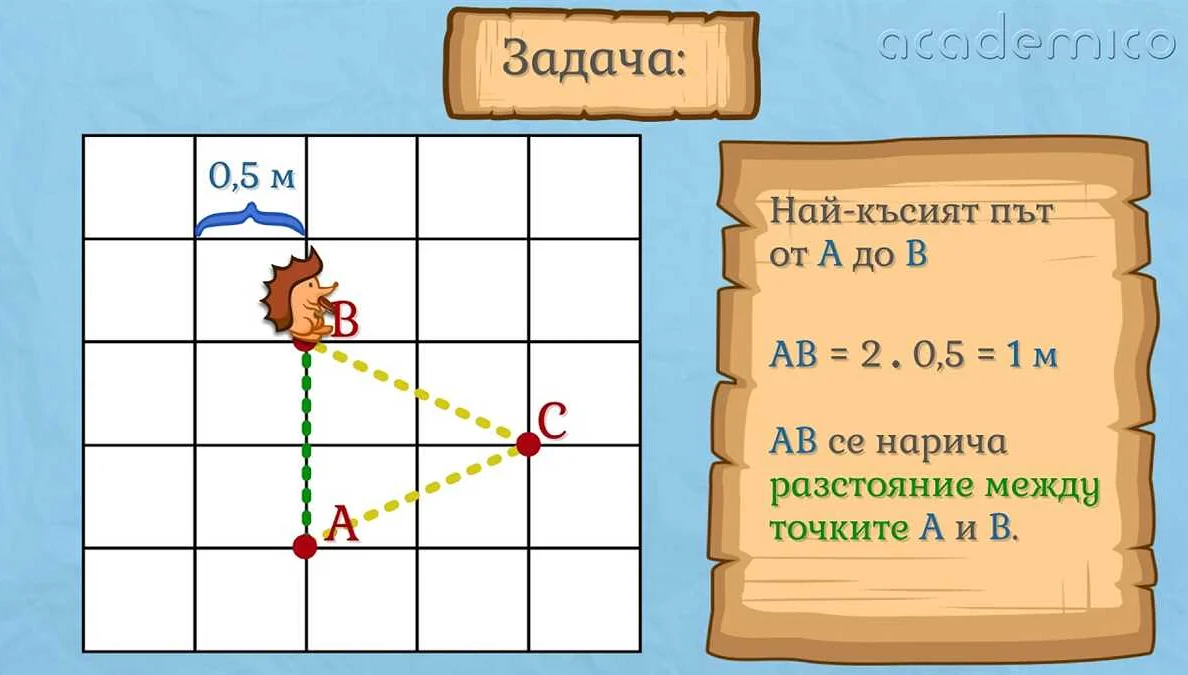


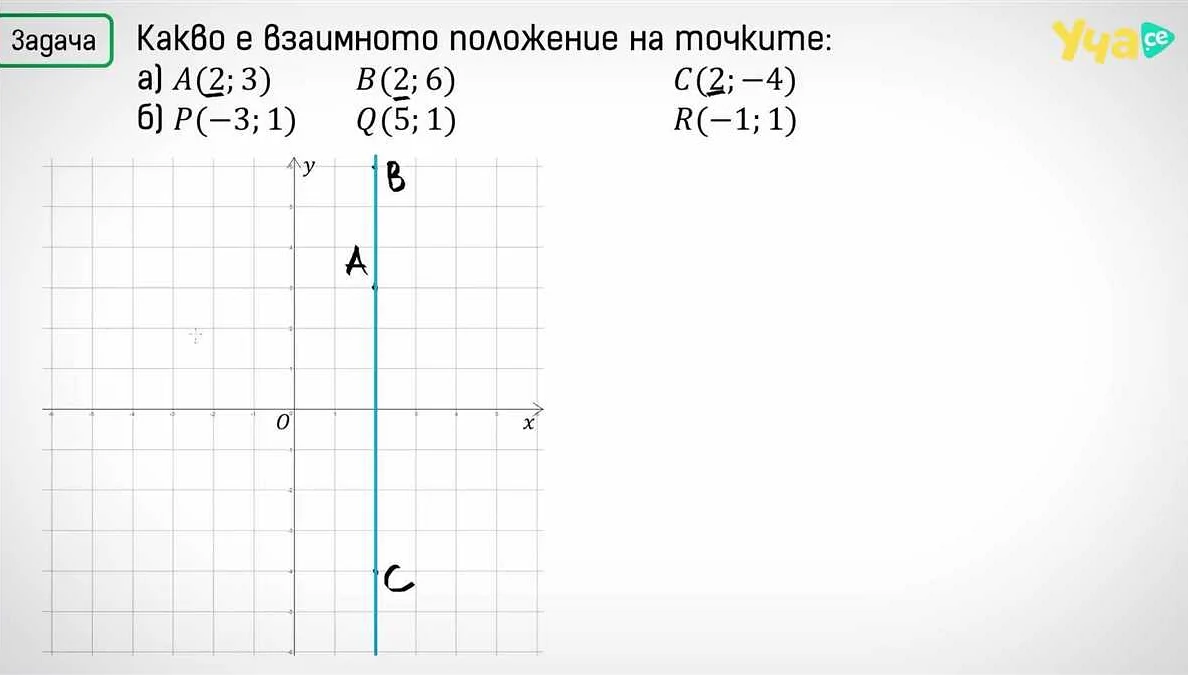
Очень интересная статья! Я всегда задаюсь вопросом, что такое координация в математике и как она применяется в 5 классе. Спасибо за подробное объяснение. Теперь я понимаю, что координация — это способность определить положение объектов на координатной плоскости. Я бы хотела узнать больше о примерах задач, чтобы лучше разобраться в этой теме. Кажется, что координация может быть полезна в повседневной жизни, например, для определения маршрута или нахождения расстояния между точками. Буду ждать продолжения статьи!