Что такое координата точки в математике

Координата точки в математике — это числовое значение, которое указывает положение точки на плоскости или в пространстве. Измеряется координата относительно некоторой точки или оси, и может быть положительной, отрицательной или нулевой. Понимание координат помогает в анализе и графическом представлении геометрических фигур и решении математических задач.

Координата точки – это числовое значение, которое указывает ее положение на плоскости или в пространстве. В математике координаты точек играют важную роль при решении геометрических задач и построении графиков функций. Понимание понятия координаты точки позволяет точно определить и описать ее местоположение.

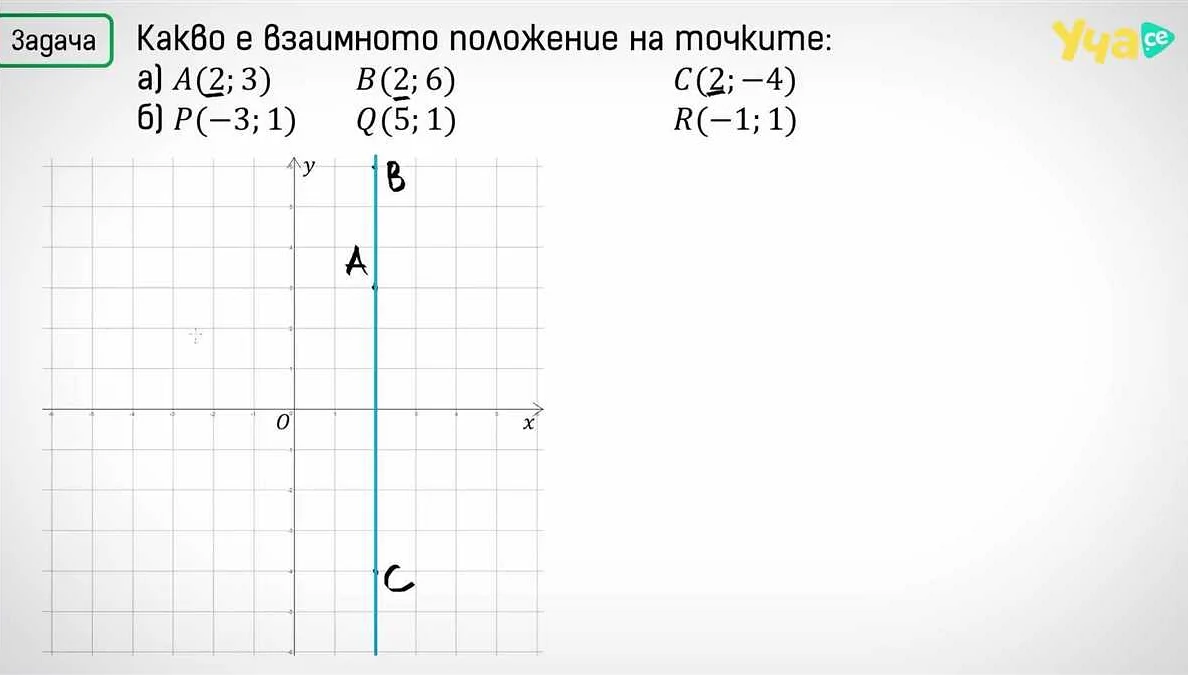
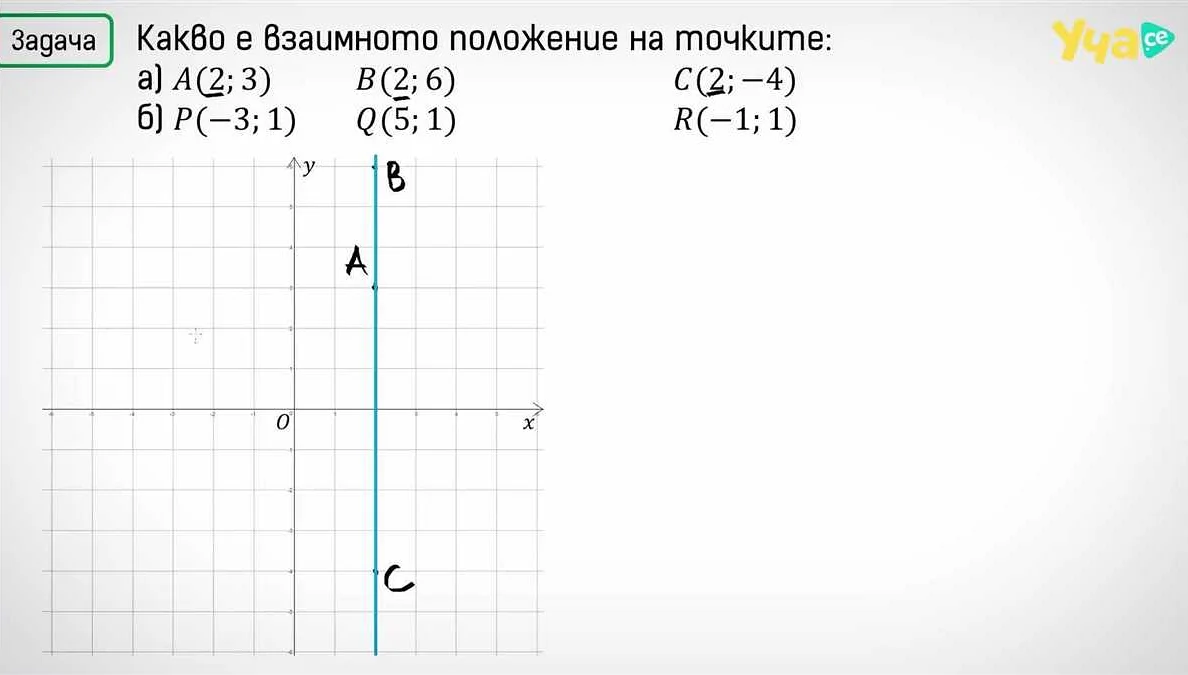
Обычно координаты точек указываются в виде упорядоченных пар или троек чисел. В двумерном пространстве каждая точка имеет две координаты – абсциссу (x-координату) и ординату (y-координату). Например, точка А с координатами (2, 5) находится на две единицы вправо от начала координат и на пять единиц вверх от него.

В трехмерном пространстве координаты точек указываются в виде троек чисел – абсциссы (x-координаты), ординаты (y-координаты) и аппликаты (z-координаты). Таким образом, каждая точка имеет свое уникальное положение в пространстве. Зная координаты точки, мы можем легко определить ее расстояние от начала координат и от других точек.

Определение координаты точки

Для удобства записи координат точек на плоскости применяются системы координат. Наиболее распространенными системами координат являются декартова система координат и полярная система координат. В декартовой системе координат точка задается парой чисел (x, y), где x — расстояние от точки до вертикальной оси (ось ординат), а y — расстояние от точки до горизонтальной оси (ось абсцисс). В полярной системе координат точка задается парой чисел (r, θ), где r — расстояние от точки до начала координат, а θ — угол между лучом, проведенным из начала координат к точке, и положительным направлением оси абсцисс.

Примеры координат точек:

• Точка A: координаты (2, 3) в декартовой системе координат на плоскости.
• Точка B: координаты (4, 5, 6) в декартовой системе координат в трехмерном пространстве.
• Точка C: координаты (3, π/4) в полярной системе координат на плоскости.

Система координат

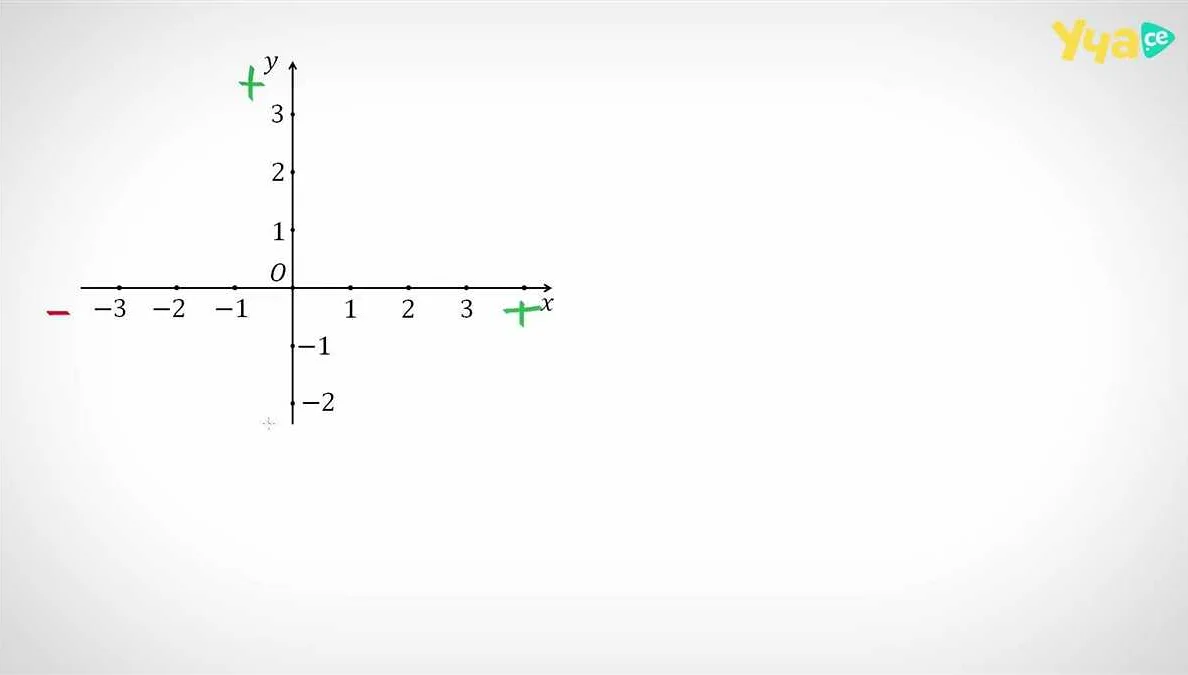
В двумерной системе координат используются две оси — ось абсцисс (Ox) и ось ординат (Oy). Они пересекаются в начале координат (точке с координатами 0,0). Каждая точка в этой системе координат может быть однозначно определена парой чисел (x,y), где x — значение по оси абсцисс, а y — значение по оси ординат.

В трехмерной системе координат добавляется еще одна ось — ось аппликат (Oz), которая перпендикулярна плоскости, образованной осью абсцисс и осью ординат. Теперь каждая точка в пространстве может быть определена тройкой чисел (x,y,z), где x — значение по оси абсцисс, y — значение по оси ординат, а z — значение по оси аппликат.

Система координат широко используется в геометрии, физике, инженерии и других науках. Она позволяет наглядно представить и анализировать различные математические и физические явления и процессы.

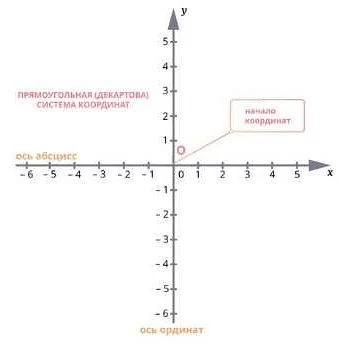
Декартова система координат

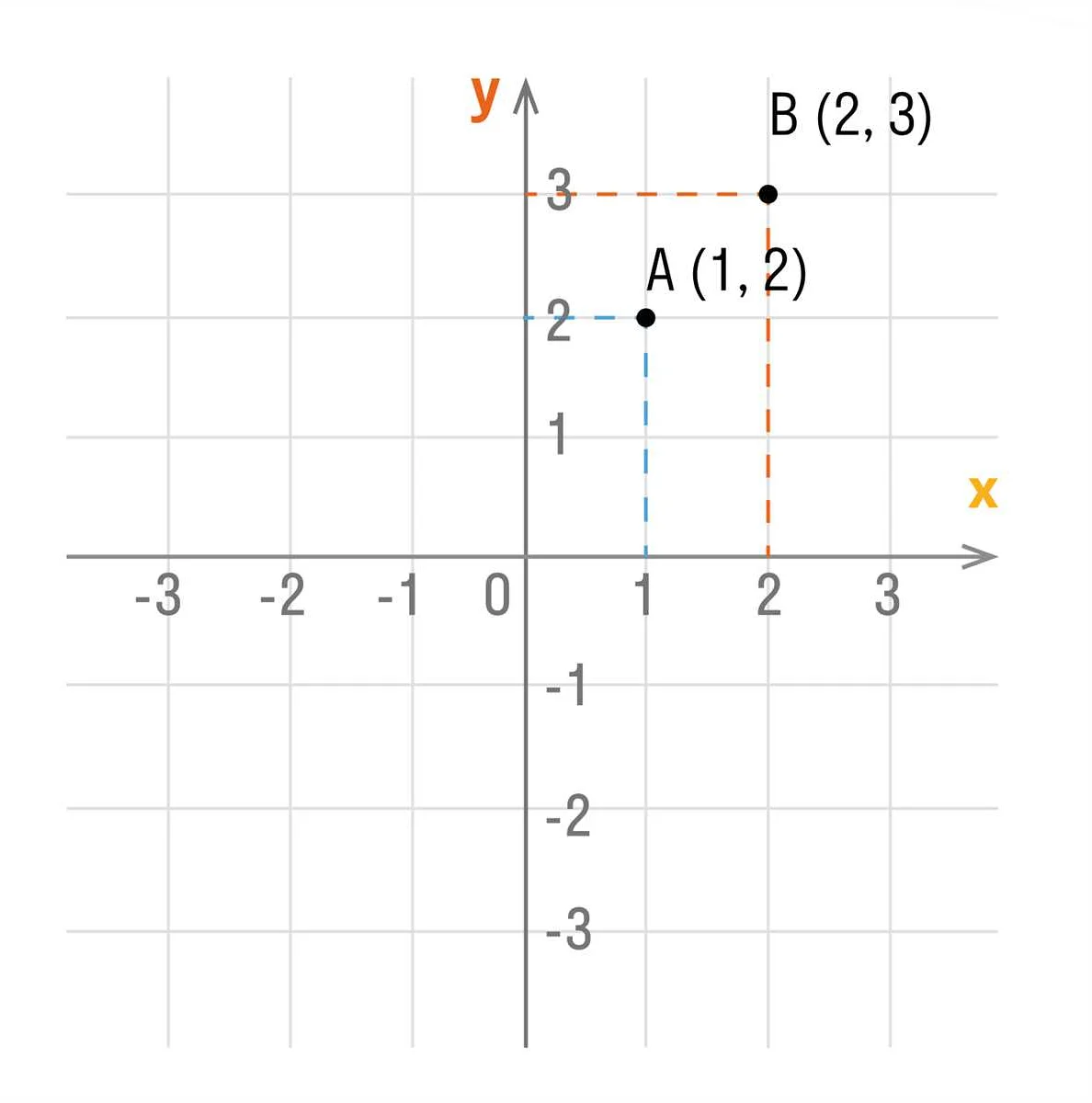
В декартовой системе координат плоскость или пространство разделены на две взаимно перпендикулярные оси – горизонтальную ось X и вертикальную ось Y. Каждая точка на плоскости или в пространстве имеет свои координаты, которые обозначаются парой чисел (X, Y) или (X, Y, Z) в трехмерном пространстве.

Ось X называется абсциссой, ось Y – ординатой, а в трехмерном пространстве добавляется еще одна ось Z, которая называется аппликатой.

Например, рассмотрим точку A, которая имеет координаты (2, 3) в декартовой системе координат. Здесь число 2 представляет собой значение абсциссы (X), а число 3 – значение ординаты (Y). Таким образом, точка A находится на плоскости на расстоянии 2 по горизонтальной оси (X) и 3 по вертикальной оси (Y).

Декартова система координат широко применяется в различных областях, таких как физика, геометрия, инженерия, информатика и другие. Она позволяет удобно описывать и анализировать положение и движение объектов в пространстве.

Полярная система координат

В поларной системе координат каждая точка плоскости представляется в виде пары чисел (r, θ), где r — радиус, а θ — угол. Радиус определяет расстояние от начала координат до точки, а угол определяет направление от начала координат до точки. Угол измеряется в радианах и может принимать значения от 0 до 2π.

Для удобства использования полярной системы координат обычно используется особый вид графика, называемый полярным графиком. На полярном графике угол изображается по горизонтальной оси, а радиус – по вертикальной оси. Таким образом, каждая точка графика имеет уникальные значения радиуса и угла, которые определяют ее положение.

Примером использования полярной системы координат может быть описание движения точки по окружности. В этом случае радиус будет постоянным (равным радиусу окружности), а угол будет меняться в зависимости от положения точки на окружности. Таким образом, каждая точка на окружности будет иметь свое уникальное значение угла и будет описываться в полярной системе координат парой (радиус окружности, угол).

Координаты в двумерном пространстве

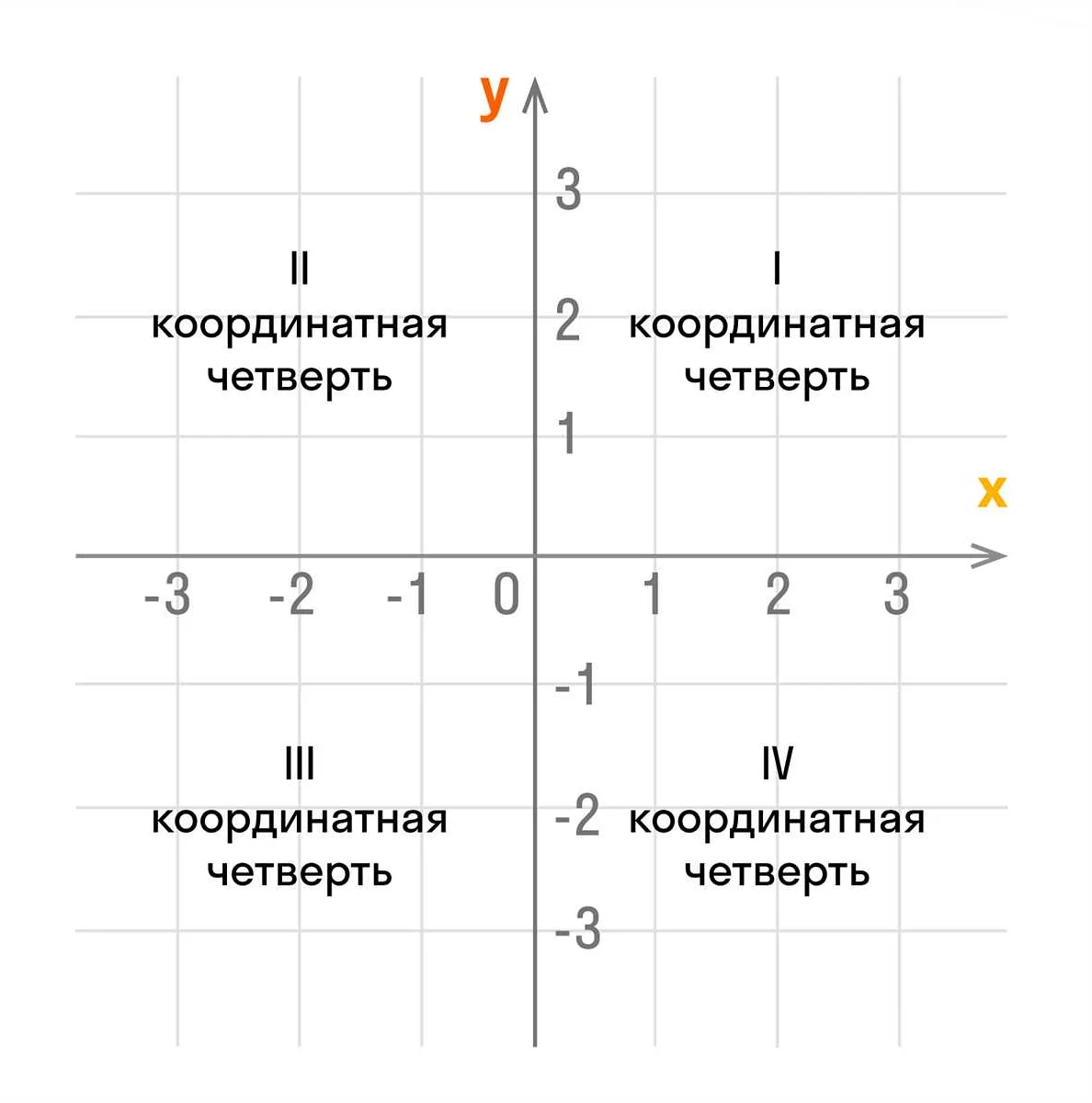
Например, если точка находится в точности в начале координат, то ее координаты будут (0, 0). Если точка находится на горизонтальной оси, то координата y будет равна 0. Аналогично, если точка находится на вертикальной оси, то координата x будет равна 0.

Координаты точки могут быть как положительными, так и отрицательными. Знак числа указывает на положение точки относительно начала координат и соответствующей оси. Если число положительное, то точка находится справа или сверху от начала координат. Если число отрицательное, то точка находится слева или снизу от начала координат.

Например, точка с координатами (3, 2) находится в третьей четверти двумерного пространства, так как обе координаты положительные, но вторая координата меньше первой. А точка с координатами (-4, -1) находится во второй четверти, так как обе координаты отрицательные, но первая координата меньше второй.

Координаты в трехмерном пространстве

Трехмерная система координат состоит из трех осей: оси x, оси y и оси z. Ось x направлена горизонтально, ось y — вертикально, а ось z — вдоль глубины. Точка в трехмерной системе координат представляется тремя числами — координатами (x, y, z).

Координата x определяет положение точки относительно оси x. Если координата x положительна, то точка находится справа от начала координат, если отрицательна — слева. Координата y определяет положение точки относительно оси y. Если координата y положительна, то точка находится выше начала координат, если отрицательна — ниже. Координата z определяет положение точки относительно оси z. Если координата z положительна, то точка находится перед началом координат, если отрицательна — за ним.

Например, точка с координатами (2, -3, 1) находится справа от начала координат на расстоянии 2 единицы по оси x, ниже начала координат на 3 единицы по оси y и перед началом координат на 1 единицу по оси z.

Трехмерная система координат широко применяется в геометрии, физике, компьютерной графике и других областях, где требуется описание положения объектов в пространстве.

Примеры координат точек в математике

В математике координаты точек определяют их положение на плоскости или в пространстве. Координаты точки задаются числами и обозначаются парой чисел в двумерном случае или тройкой чисел в трехмерном случае.

Ниже приведены несколько примеров координат точек:

• Точка A на плоскости с координатами (2, 3). Это означает, что точка A находится на расстоянии 2 единиц по оси x и 3 единиц по оси y от начала координат.
• Точка B в трехмерном пространстве с координатами (1, -2, 5). Здесь первая координата указывает расстояние по оси x, вторая — по оси y, а третья — по оси z.
• Точка C на плоскости с координатами (-4, 0). Это означает, что точка C находится на расстоянии 4 единиц влево от начала координат по оси x и находится на оси y.

Координаты точек позволяют однозначно определить их положение и использовать их для решения различных задач в математике.

Вопрос-ответ:

Что такое координата точки в математике?

Координата точки в математике — это числовое значение, которое определяет положение точки на плоскости или в пространстве. В двумерном случае координаты точки состоят из двух чисел — абсциссы и ординаты, а в трехмерном случае добавляется еще одна координата — аппликата.

Как определить координаты точки на плоскости?

Для определения координат точки на плоскости используется прямоугольная система координат. Одна координата — абсцисса — определяется расстоянием от точки до вертикальной оси, а вторая координата — ордината — определяется расстоянием от точки до горизонтальной оси.

Как можно представить координаты точки графически?

Координаты точки на плоскости могут быть представлены графически с помощью точки на координатной плоскости. Абсцисса точки определяет ее положение относительно вертикальной оси, а ордината — относительно горизонтальной оси.

Какие примеры можно привести для понимания координат точки?

Примеры координат точек на плоскости могут быть следующими: точка A с координатами (2, 3), точка B с координатами (-1, 4), точка C с координатами (0, -2). Эти координаты указывают на положение каждой точки относительно осей координат.

Какие еще системы координат существуют в математике, кроме прямоугольной?

Помимо прямоугольной системы координат, существуют также полярная система координат, цилиндрическая система координат и сферическая система координат. В каждой из этих систем координат координаты точек определяются по-разному и используются для решения различных задач.

Видео по теме: