Что такое корень математика 6 класс

Корень в математике 6 класса — это число, которое при возведении в квадрат дает заданное число. Учебная программа предусматривает изучение понятия корня, его свойств и способов нахождения в 6 классе. В статье рассмотрены основные темы, связанные с корнем: определение, примеры, основные свойства и применение в решении уравнений и задач. Узнайте, как правильно находить корень и освойте эту важную тему математики 6 класса.

Корень — это одно из основных понятий в математике, с которым каждый ученик сталкивается уже в 6 классе. Корень является обратной операцией к возведению в квадрат и представляет собой число, которое при возведении в квадрат даст исходное число.

В математике корень обозначается символом √ и записывается перед числом, из которого берется корень. Например, корень из числа 9 записывается как √9 и равен 3, так как 3 × 3 = 9.

Корень может быть извлечен из любого положительного числа, кроме нуля. Он может быть также рациональным и иррациональным числом. Рациональные числа имеют конечное или периодическое десятичное представление, тогда как иррациональные числа имеют бесконечное и непериодическое десятичное представление.

Корень имеет несколько свойств, которые помогают упростить вычисления. Например, можно перемножать числа под корнем и выносить из них общий множитель. Также можно складывать и вычитать числа под корнем с одинаковыми иррациональными слагаемыми. Эти свойства позволяют упростить сложные задачи и сделать вычисления более точными.

В заключение, корень является одним из основных понятий в математике, которое помогает нам решать различные задачи и совершать точные вычисления. Понимание его свойств и правил его использования позволяет ученикам 6 класса успешно справляться с математическими заданиями и развивать свои навыки в этой области.

Определение корня

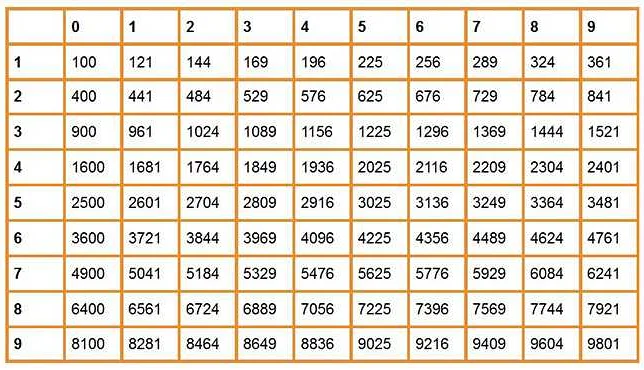
Например, корень квадратный из числа 9 равен 3, так как 3 × 3 = 9. В этом случае число 9 является радикандом, а корень 3 – корнем квадратным.

Корень может быть любой степени. Например, корень кубический из числа 8 равен 2, так как 2 × 2 × 2 = 8. В этом случае число 8 является радикандом, а корень 2 – корнем кубическим.

Корень может быть как положительным, так и отрицательным. Например, корень квадратный из числа 16 может быть как 4, так и -4, так как 4 × 4 = 16 и (-4) × (-4) = 16. В этом случае число 16 является радикандом, а корни 4 и -4 – корнями квадратными.

Свойства корня

• Квадратный корень из нуля равен нулю: √0 = 0.
• Квадратный корень из единицы равен единице: √1 = 1.
• Квадратный корень из числа, возведенного в квадрат, равен модулю этого числа: √(x^2) = |x|.
• Квадратный корень из произведения двух чисел равен произведению квадратных корней от каждого из этих чисел: √(a * b) = √a * √b.
• Квадратный корень из частного двух чисел равен частному квадратных корней от каждого из этих чисел: √(a / b) = √a / √b.
• Квадратный корень из числа, возведенного в n-ную степень, равен корню из этого числа, возведенного в n/2-ую степень: √(x^n) = (x^(n/2)).
• Корень из корня равен корню соответствующей степени произведения исходных корней: √(√a) = ((a^(1/n))^m) = a^(1/(n*m)).
• Корень из отрицательного числа является мнимым числом или комплексным числом.

Знание этих свойств поможет нам с легкостью работать с корнями и использовать их в решении различных математических задач.

Корень квадратный

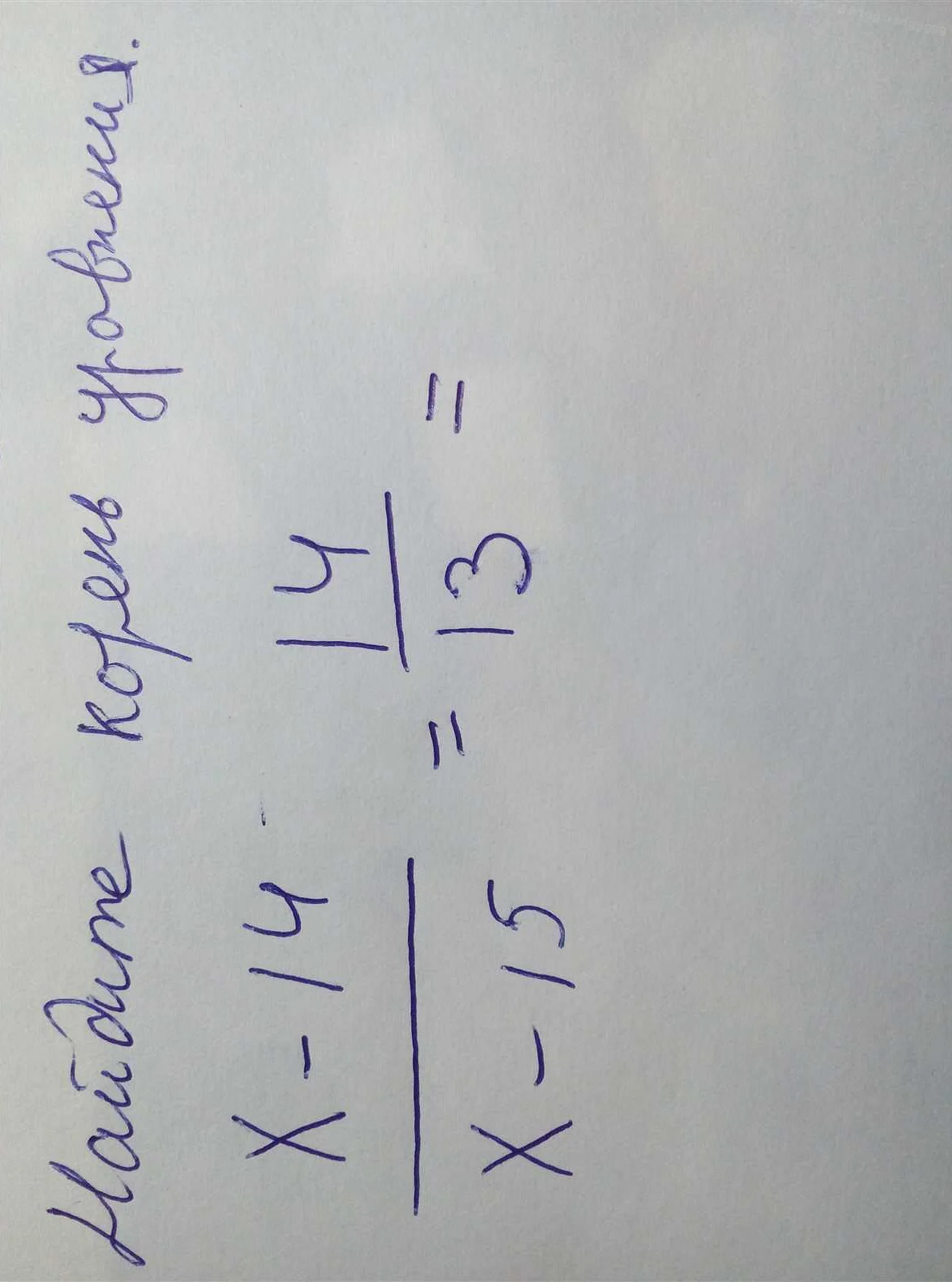
Математически корень квадратный обозначается символом √. Например, корень квадратный из числа 9 записывается как √9 и равен 3, так как 3 * 3 = 9.

Основные свойства корня квадратного:

• Корень квадратный из отрицательного числа является мнимым числом, так как квадрат мнимого числа всегда отрицательный.
• Корень квадратный из нуля равен нулю, так как 0 * 0 = 0.
• Корень квадратный из положительного числа всегда положителен.
• Корень квадратный из числа больше 1 всегда меньше самого числа.

Примеры:

• √16 = 4, так как 4 * 4 = 16.
• √25 = 5, так как 5 * 5 = 25.
• √36 = 6, так как 6 * 6 = 36.

Примеры корней

Рассмотрим несколько примеров корней:

Пример 1: Корень из числа 25 равен 5, так как 5 * 5 = 25.

Пример 2: Корень из числа 16 равен 4, так как 4 * 4 = 16.

Пример 3: Корень из числа 9 равен 3, так как 3 * 3 = 9.

Пример 4: Корень из числа 36 равен 6, так как 6 * 6 = 36.

Корни могут быть как целыми числами, так и десятичными дробями. Например, корень из числа 2 не является целым числом и равен примерно 1,414.

Примечание: Для взятия корня из числа в математике используют специальную функцию или калькулятор.

Корень n-ой степени

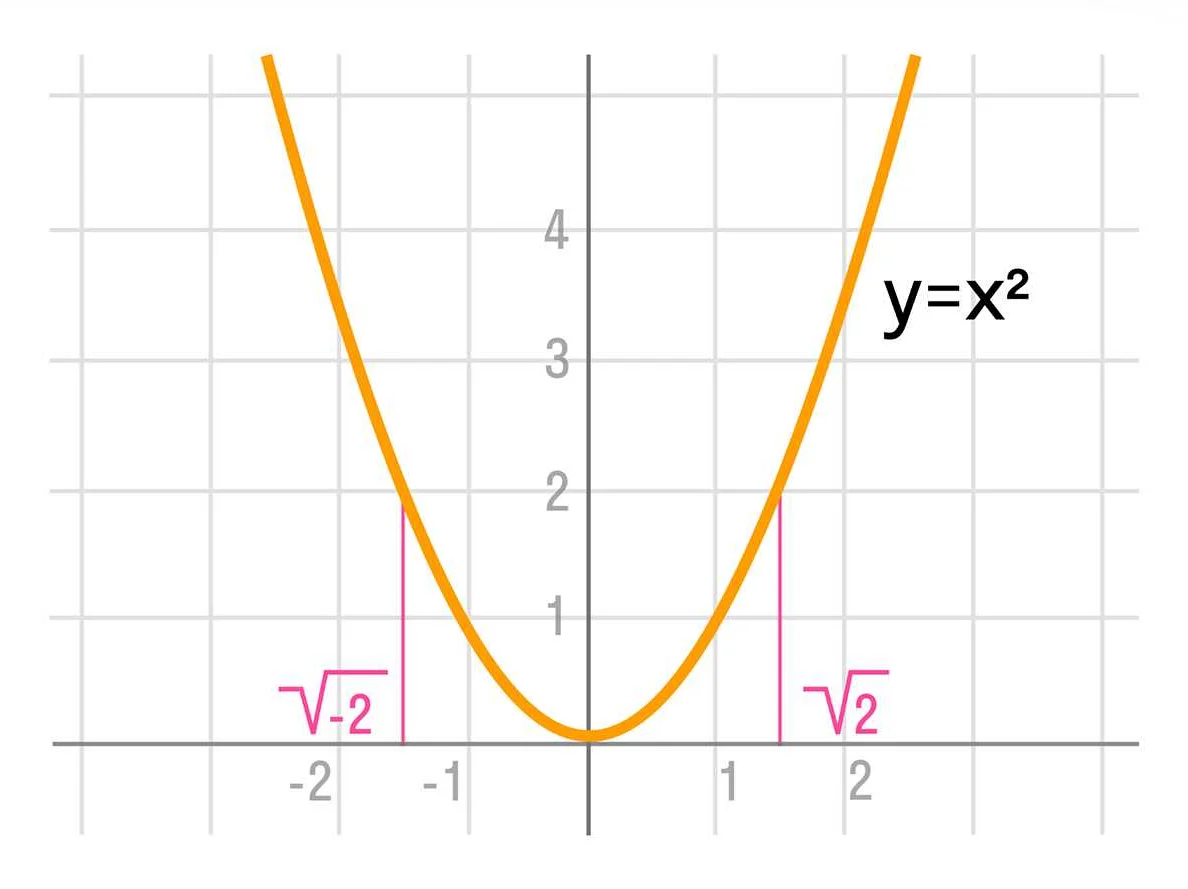
Для того чтобы найти корень n-ой степени из числа, нужно найти число, возведение которого в степень n даст это число.

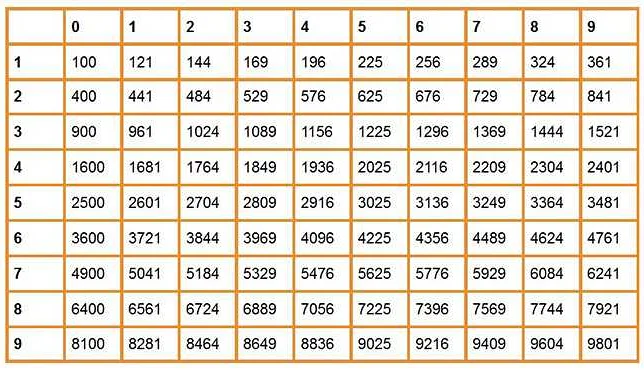
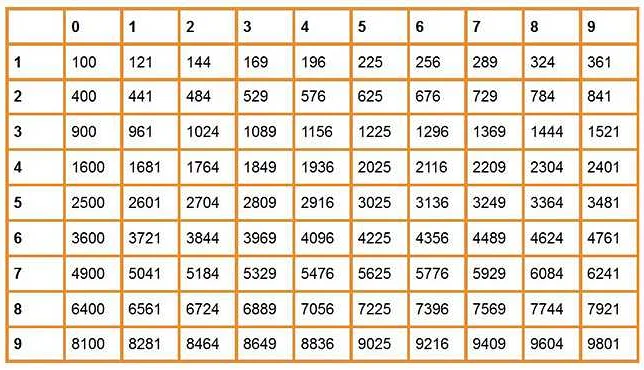
Корень n-ой степени может быть найден с использованием таблицы квадратных корней или калькулятора.

Свойства корня n-ой степени:

• Если n — четное число, то корень n-ой степени из отрицательного числа равен несуществующему комплексному числу.
• Если n — нечетное число, то корень n-ой степени из отрицательного числа равен отрицательному числу.
• Корень n-ой степени из 0 всегда равен 0.
• Корень n-ой степени из 1 всегда равен 1.

Например:

√3 8 = 2, так как 2^3 = 8.

√2 16 = 4, так как 4^2 = 16.

√4 81 = 3, так как 3^4 = 81.

Свойства корня n-ой степени

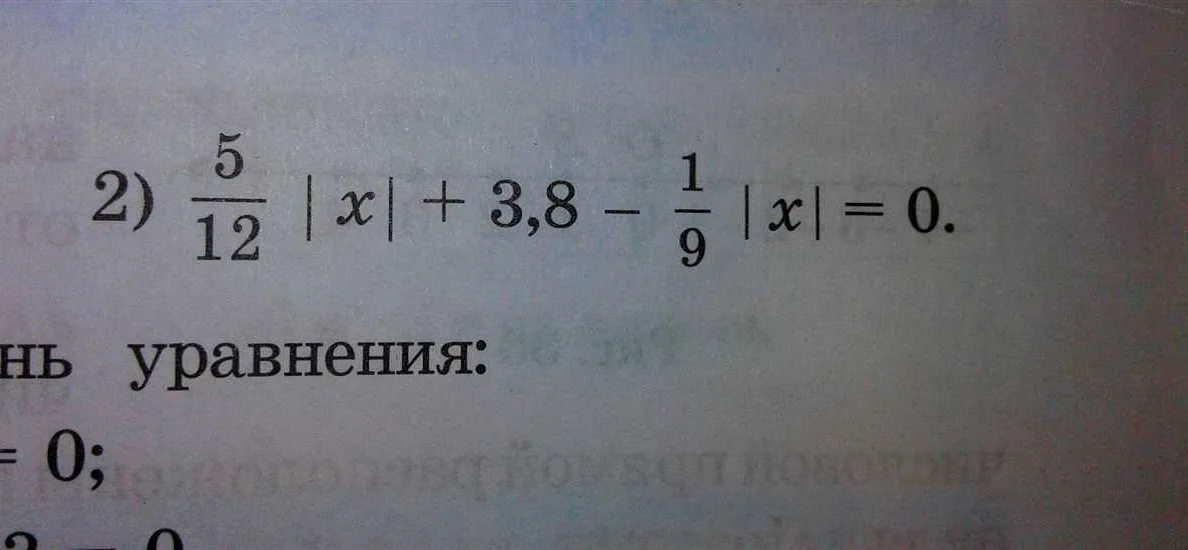
2. Свойство умножения: Корень n-ой степени от произведения двух чисел равен произведению корней n-ой степени от этих чисел.

3. Свойство возведения в степень: Корень n-ой степени от числа, возведенного в степень m, равен числу, возведенному в степень m/n.

4. Свойство отношения: Корень n-ой степени от дроби равен дроби, у которой числитель и знаменатель возведены в корень n-ой степени.

5. Свойство сложения: Корень n-ой степени от суммы двух чисел равен сумме корней n-ой степени от этих чисел.

6. Свойство деления: Корень n-ой степени от частного двух чисел равен частному корней n-ой степени от этих чисел.

7. Свойство корня из корня: Корень n-ой степени от корня m-ой степени от числа равен корню из произведения n и m степеней от этого числа.

8. Свойство равенства: Если корень n-ой степени от числа равен другому числу, то это число возводится в степень n.

Пример: Корень кубический из 8 равен 2, потому что 2^3 = 8.

Примеры корней n-ой степени

1. Корень квадратный (√2): это число, при возведении в квадрат дает 2. Таким образом, √2 ≈ 1,414.
2. Корень кубический (∛8): это число, при возведении в куб дает 8. Таким образом, ∛8 = 2.
3. Корень четвертой степени (∜16): это число, при возведении в четвертую степень дает 16. Таким образом, ∜16 = 2.
4. Корень пятой степени (∛32): это число, при возведении в пятую степень дает 32. Таким образом, ∛32 ≈ 2,828.

Примеры корней n-ой степени помогают нам понять, как использовать корень в математике. Они являются основой для более сложных вычислений и решения уравнений.

Видео по теме:

Что такое корень в математике?

Корень в математике — это операция, обратная возведению в степень. Если число а возведено в какую-то степень и получено число b, то корнем из b называется такое число x, что x возводя в ту же степень, получим число b. Например, корнем числа 9 будет число 3, так как 3 возводя во вторую степень, равно 9.

Можно ли извлечь корень из отрицательного числа?

В обычной арифметике корень из отрицательного числа не определен. Однако, в математике существует понятие комплексных чисел, которые позволяют извлекать корень из отрицательных чисел. Например, корнем из -9 будет число 3i, где i — мнимая единица, так как (3i)^2 равно -9.

Где в повседневной жизни можно применить знание о корнях в математике?

Знание о корнях в математике может быть полезным во многих ситуациях повседневной жизни. Например, при решении задач по геометрии, при расчете площади круга или длины стороны квадрата, при решении задач по физике, при построении графиков функций и т.д. Корни также используются в других областях науки, таких как инженерия и экономика.

Что такое корень в математике 6 класс?

Корень в математике 6 класс – это такое число, при возведении которого в квадрат получается исходное число. Например, корень из числа 9 равен 3, так как 3^2 = 9.

Какие свойства имеет корень в математике?

Корень в математике обладает несколькими свойствами. Одно из них – корень суммы равен сумме корней. Другое свойство – корень произведения равен произведению корней. Кроме того, корень из произведения равен корню из каждого сомножителя. Например, корень из (5 + 3) равен корню из 5 плюс корню из 3.