Корень в математике как решать

Узнайте, как решать корни в математике: научитесь вычислять корень квадратный, корень третий и другие степенные корни. Познакомьтесь с основными методами и правилами, позволяющими с легкостью находить значения корней в различных задачах и уравнениях. Получите необходимые инструменты для успешного решения задач, связанных с корнями в математике.

Корень – одно из основных понятий в математике, которое широко используется при решении различных задач. Корень является обратной операцией в отношении возведения в степень. Он позволяет найти число, которое возведенное в определенную степень, равно данному числу.

Для нахождения корня из числа необходимо использовать специальный математический символ – знак радикала (√). Корень может быть любой степени, но самыми распространенными являются квадратный корень (√), кубический корень (∛) и корень четвертой степени (∜).

Решение задач на корень требует знания основных свойств корней. Например, умножение числа на корень из него самого дает исходное число, а возведение корня в степень эквивалентно извлечению исходного числа из под корня. Благодаря этим свойствам, можно решать различные уравнения, вычислять площади и объемы геометрических фигур, находить значения функций и многое другое.

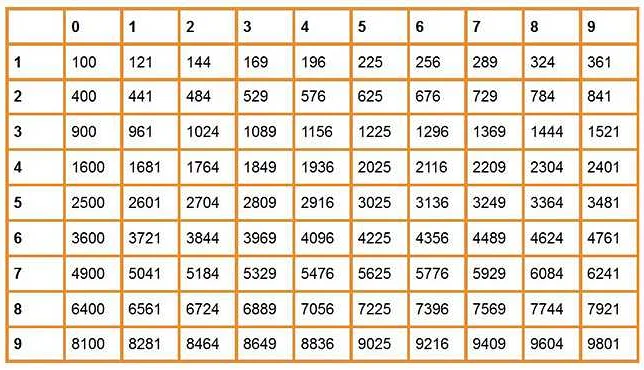
Например, если нам нужно найти квадратный корень (√) из числа 25, то мы должны найти такое число, которое при возведении во вторую степень будет равно 25. В данном случае квадратный корень из 25 равен 5, так как 5² = 25.

Корень в математике является важным инструментом для решения различных задач. Он позволяет найти числа, которые удовлетворяют определенным условиям и являются решениями уравнений или задач. Понимание особенностей и применение корней помогает в повседневной жизни, в научных и инженерных расчетах, а также в других областях, где требуются точные и надежные результаты.

Что такое корень в математике?

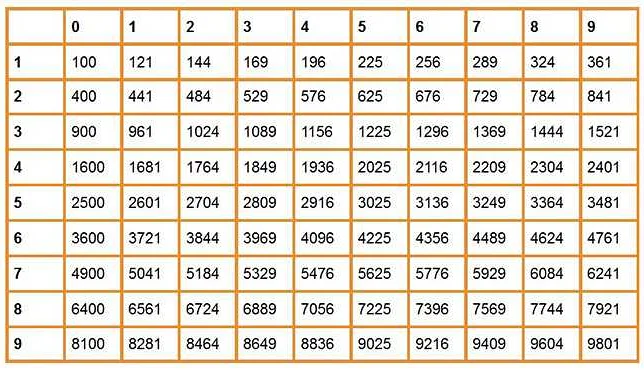
Корень обозначается символом √ и пишется перед выражением, из которого извлекается корень. Например, корень из числа 4 обозначается как √4 и равен 2, так как 2 * 2 = 4.

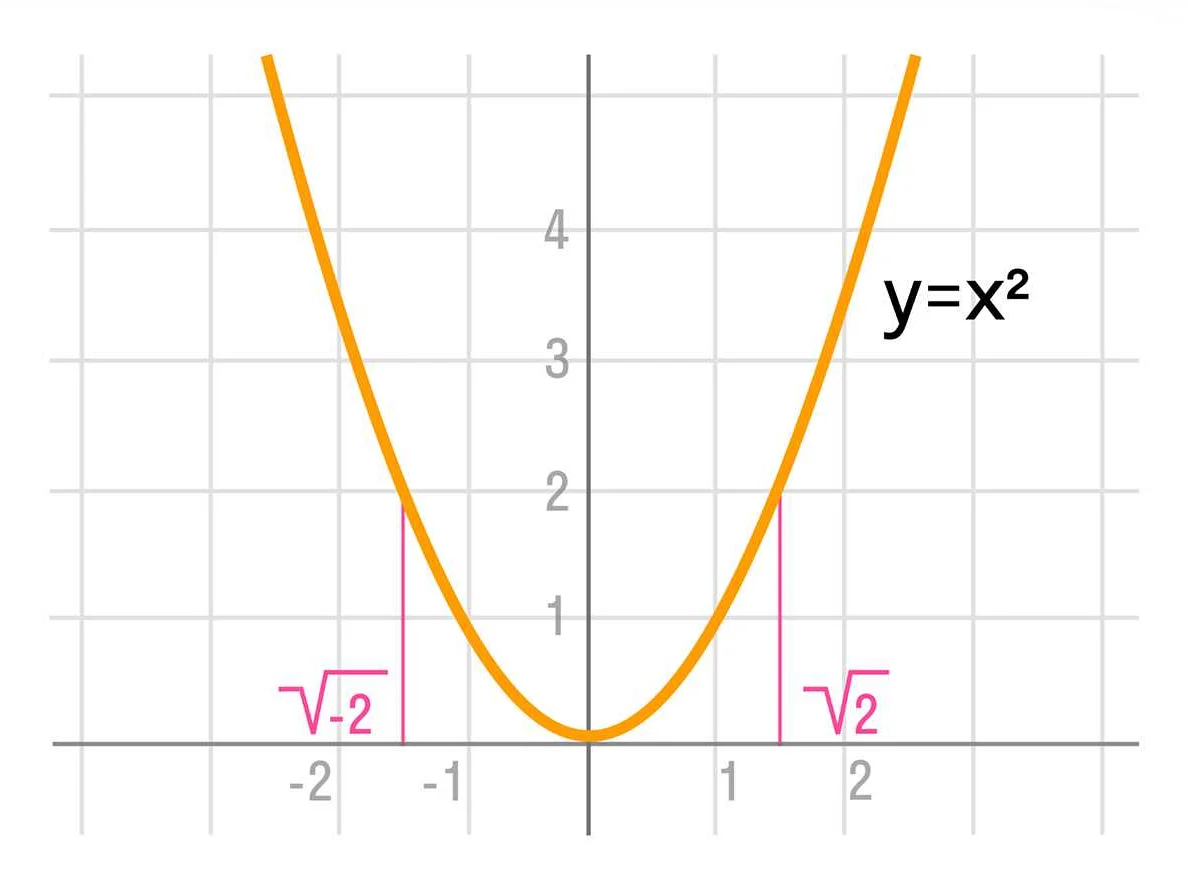
Корень может быть как целым, так и десятичным числом. Например, корень из числа 9 равен 3, а корень из числа 2 равен приблизительно 1,414.

Корень может быть извлечен из любого положительного числа. Если число отрицательное, то корень из него является комплексным числом.

Основные свойства корня в математике:

СвойствоФормула

Корень из произведения	√(a * b) = √a * √b
Корень из частного	√(a / b) = √a / √b
Корень из степени	√(a^b) = a^(b/2)
Корень из корня	√(√a) = a^(1/4)

Корни в математике широко используются при решении уравнений, построении графиков, анализе данных и других задачах. Знание основных свойств корня позволяет более эффективно выполнять математические операции и решать задачи.

Как решать корень

Для решения корня необходимо использовать следующие шаги:

1. Запишите заданное значение корня.
2. Разделите значение корня на простые множители и определите, есть ли среди них повторяющиеся множители.
3. Разделите значение корня на каждый повторяющийся множитель, возведя его в степень, равную количеству повторений.
4. Вычислите корни от каждого множителя и запишите результат.
5. Если возникло отрицательное число под знаком корня, то решение невозможно, так как корень из отрицательного числа является комплексным числом.

Пример решения корня:

1. Решим корень из числа 16. Запишем √16.
2. Разделим 16 на простые множители: 16 = 2 × 2 × 2 × 2.
3. Разделим 16 на каждый множитель: √16 = √2 × 2 × 2 × 2.
4. Вычислим корень от каждого множителя: √16 = 2 × 2 × 2 × 2 = 4 × 2 = 8.

Таким образом, корень из числа 16 равен 8.

Решение корня может быть более сложным в случае, если значение под знаком корня является десятичной дробью или дробным числом. В таких случаях необходимо использовать специальные методы, такие как методы приближенного вычисления или использование калькуляторов, способных обрабатывать десятичные числа.

Примеры решения корня

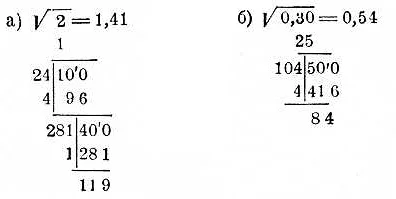
ПримерРезультат

√4	2
√9	3
√16	4
√25	5

В данных примерах мы находим квадратный корень из чисел 4, 9, 16 и 25. Результатом решения является число, которое при возведении в квадрат дает исходное число. Так, √4 = 2, потому что 2^2 = 4.

При решении корня важно помнить, что квадратный корень из отрицательного числа не определен в множестве вещественных чисел, но может быть определен в множестве комплексных чисел.

Особенности использования корня в математике

Использование корня в математике имеет несколько особенностей:

Особенность	Пример
1. Извлечение корня из отрицательного числа	√(-9) не имеет действительного значения, так как квадратный корень из отрицательного числа – комплексное число.
2. Корни с нечетной степенью	√8 = 2√2. Корень с нечетной степенью можно представить в виде произведения корня с четной степенью и корня с единичной степенью.
3. Корни с четной степенью	√16 = 4. Корень с четной степенью всегда имеет одно вещественное значение.
4. Использование индексов	n√a, где n – индекс корня, a – число. Индекс корня определяет степень корня и количество решений.

Понимание особенностей использования корня в математике позволяет правильно решать задачи, связанные с извлечением корней и использованием корней в различных математических операциях.

Корень как элемент уравнения

Решение уравнений с корнем часто требует использования алгебраических методов. Например, чтобы решить уравнение вида √x = a, нужно возвести обе части уравнения в квадрат: (√x)^2 = a^2. Полученное уравнение x = a^2 будет иметь единственное решение.

Особенностью уравнений с корнем является необходимость проверки полученных решений на корректность. Иногда возникают случаи, когда полученное значение является экстремальным, и при подстановке в исходное уравнение оно не удовлетворяет условиям задачи.

Важно помнить, что корень может быть как положительным, так и отрицательным. При решении уравнений с корнем всегда нужно учитывать оба возможных значения.

Примеры уравнений с корнем:

1. √x = 2 — решение: x = 4 (поскольку 2^2 = 4).
2. √(x+1) = -3 — нет решений, поскольку квадратный корень из неотрицательного числа всегда положителен.
3. √(x-5) = -2 — нет решений, поскольку квадратный корень из отрицательного числа является комплексным числом.

Решение уравнений с корнем требует аккуратности и внимательности, особенно при работе с отрицательными числами и комплексными числами. Правильное понимание и применение этих особенностей помогут успешно решить сложные уравнения.

Использование корня в геометрии

Корень в математике находит широкое применение не только в алгебре и арифметике, но и в геометрии. В геометрии корень используется для решения различных задач, связанных с вычислением площадей, длин отрезков и других геометрических параметров.

Одним из примеров использования корня в геометрии является вычисление длины диагонали прямоугольника. Если известны длины его сторон a и b, то длина диагонали d может быть найдена по формуле:

ФормулаОписание

d = √(a^2 + b^2)

Формула для вычисления длины диагонали прямоугольника

Еще одним примером использования корня в геометрии является нахождение радиуса окружности, описанной вокруг треугольника. Если известны длины сторон треугольника a, b и c, то радиус R окружности может быть найден по формуле:

ФормулаОписание

R = abc / 4S

Формула для вычисления радиуса окружности, описанной вокруг треугольника

Здесь S — площадь треугольника, которая может быть найдена с использованием формулы Герона:

ФормулаОписание

S = √(p(p-a)(p-b)(p-c))

Формула Герона для вычисления площади треугольника

где p — полупериметр треугольника, который вычисляется по формуле:

ФормулаОписание

p = (a + b + c) / 2

Формула для вычисления полупериметра треугольника

Таким образом, корень в геометрии позволяет решать различные задачи, связанные с вычислением геометрических параметров треугольников, прямоугольников и других фигур.

Применение корня в физике

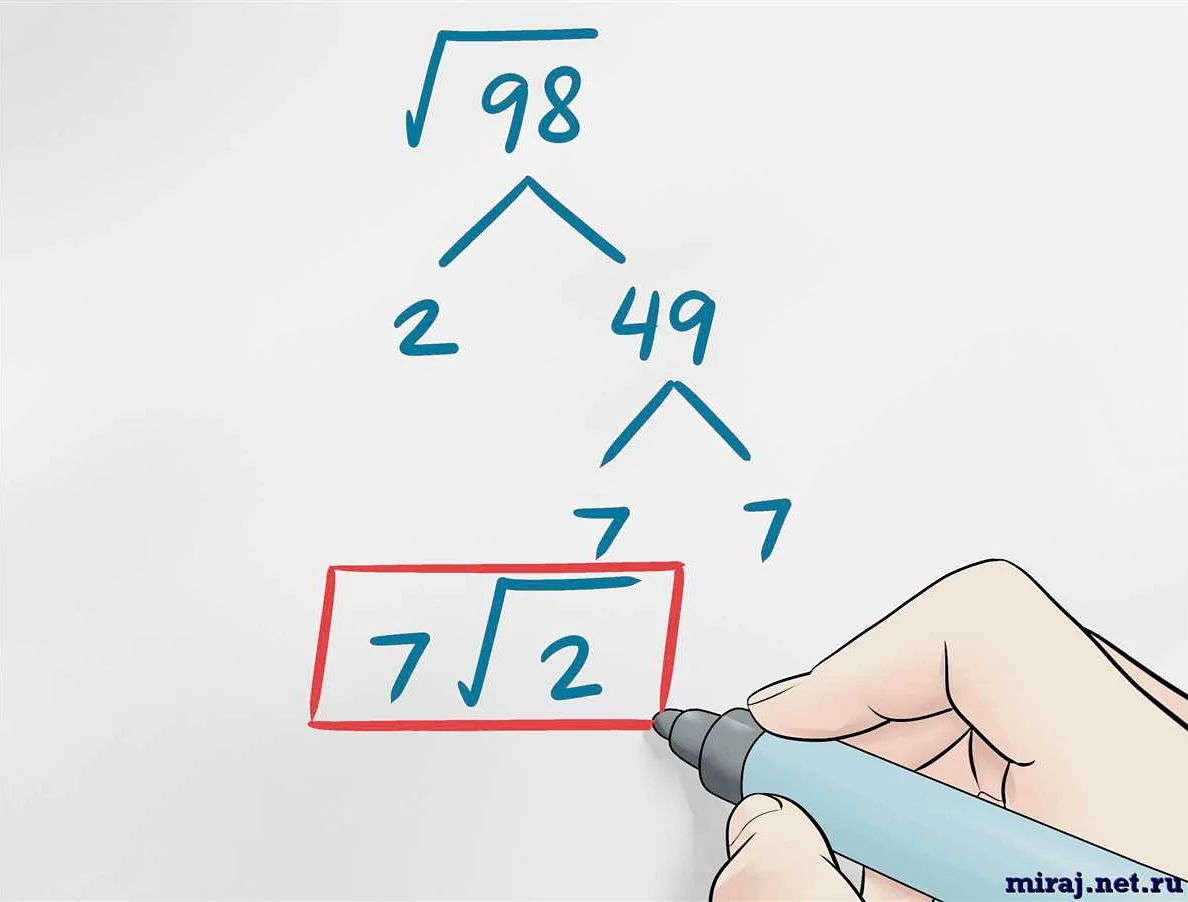
Корень в математике находит свое применение не только в арифметических вычислениях, но и в физике. Он позволяет решать различные физические задачи и находить значения неизвестных величин.

Один из примеров применения корня в физике — нахождение скорости тела при свободном падении. Формула для вычисления скорости падения тела связана с корнем. Скорость падения можно найти, используя формулу:

v = √(2 * g * h),

где v — скорость падения, g — ускорение свободного падения, h — высота падения.

Корень также применяется при решении задач о движении тела по параболе. Например, чтобы найти время полета тела, можно воспользоваться формулой:

t = 2 * √(h / g),

где t — время полета, h — высота полета, g — ускорение свободного падения.

Кроме того, корень используется при решении задач о колебаниях и волнах. Например, при расчете периода колебаний математического маятника или гармонического осциллятора используется формула:

T = 2π * √(l / g),

где T — период колебаний, l — длина маятника, g — ускорение свободного падения.

Применение корня в физике позволяет упростить решение задач и получить точные значения физических величин. Знание математических операций и умение применять их в физических расчетах являются важными навыками для физиков и инженеров.

Вопрос-ответ:

Как решить квадратное уравнение с корнями?

Для решения квадратного уравнения с корнями нужно использовать формулу дискриминанта. Если уравнение имеет вид ax^2 + bx + c = 0, то дискриминант вычисляется по формуле D = b^2 — 4ac. Если D > 0, то уравнение имеет два различных корня, если D = 0, то уравнение имеет один корень, а если D < 0, то уравнение не имеет действительных корней.

Как найти значение корня из числа?

Для нахождения значения корня из числа можно воспользоваться калькулятором или математической программой, которая имеет функцию извлечения корня. Вручную можно использовать методы приближения, такие как метод Ньютона. Например, чтобы найти корень квадратный из числа 9, нужно найти число, которое при возведении в квадрат будет равно 9. В данном случае корень квадратный из 9 равен 3.

Как найти корень из отрицательного числа?

Корень из отрицательного числа не является действительным числом. В обычной арифметике корень из отрицательного числа не определен. Однако, в математике существуют комплексные числа, которые позволяют находить корень из отрицательных чисел. Корень из отрицательного числа a можно найти в виде комплексного числа z, такого что z^2 = a. Например, корень из -4 равен 2i, где i — мнимая единица.

Как свести выражение с корнем к уравнению?

Для сведения выражения с корнем к уравнению нужно возвести обе части выражения в квадрат. Например, если дано выражение √x = a, где a — известное число, то возводим обе части в квадрат: (√x)^2 = a^2. Получаем уравнение x = a^2. Таким образом, свели выражение с корнем к уравнению.

Различные виды корней в математике

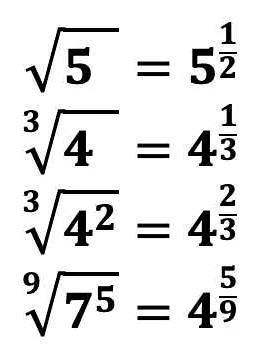
Квадратный корень — это операция, обратная возведению в квадрат. Если число а является квадратом числа b, то квадратный корень из b равен а. Квадратный корень обозначается символом √ и записывается как √b.

Кубический корень — это операция, обратная возведению в куб. Если число а является кубом числа b, то кубический корень из b равен а. Кубический корень обозначается символом √3 и записывается как ∛b.

N-ный корень — это операция, обратная возведению в степень n. Если число а является степенью числа b, то n-ный корень из b равен а. N-ный корень обозначается символом √n и записывается как √nb.

Важно отметить, что корни могут быть как положительными, так и отрицательными числами, в зависимости от значения исходного числа. Также следует учитывать, что некоторые числа не имеют рациональных корней и могут быть представлены только в виде иррациональных чисел.

Видео по теме: