Что такое корень в математике 8 класс для тупых

В данной статье объясняется, что такое корень в математике для учащихся 8 класса с простыми и понятными примерами и объяснениями. Это позволит даже самым неопытным и тупым ученикам легко понять и освоить понятие корня в математике.

В математике особое внимание уделяется понятию корня. Корень — это математическая операция, обратная возведению в степень. В 8 классе ученики начинают изучать различные типы корней и их свойства.

Корень из числа можно представить в виде дроби, где числитель — это число, из которого извлекается корень, а знаменатель — это показатель корня. Например, корень квадратный из числа 9 равен 3, так как 3 * 3 = 9. Корень квадратный обозначается символом √.

Однако, помимо квадратного корня, существуют и другие типы корней, такие как кубический корень, корень n-ной степени и т.д. Каждый из них имеет свои особенности и правила вычисления.

Изучение корней в математике 8 класса позволяет ученикам углубить свои знания о числах и их свойствах, а также научиться решать более сложные задачи, связанные с корнями и степенями.

Понимание и умение работать с корнями является важной базой для дальнейшего изучения математики и решения задач различной сложности. Поэтому в 8 классе особое внимание уделяется этой теме, чтобы обеспечить ученикам качественную подготовку к изучению более продвинутых математических концепций.

Определение корня в математике

В математике понятие «корень» имеет несколько значений. В данном контексте мы рассмотрим определение корня как обратной операции возведения в степень.

Корень числа a – это такое число x, что его возведение в n-ую степень равно a. То есть, если x^n = a, то x называется корнем числа a степени n.

Корень можно представить в виде дроби или в виде десятичной дроби, в зависимости от того, является ли число a рациональным или иррациональным.

Если мы говорим о корне n-ой степени из отрицательного числа, то используем понятие комплексного числа. Комплексный корень может иметь два значения – положительное и отрицательное.

Корни чисел являются важным понятием в математике и широко используются в различных областях, таких как алгебра, геометрия и физика.

Зачем нужен корень в математике

Основное назначение корня – извлечение квадратного, кубического и других корней из чисел. Например, если мы знаем, что площадь квадрата равна 36, то мы можем найти длину его стороны, взяв корень из 36. Корень также может помочь нам найти значение переменной в уравнении, если известно, что эта переменная возводится в степень.

Корень также используется для решения задач, связанных с процентами и процентными значениями. Например, если мы знаем, что число увеличилось на 20% и хотим найти исходное значение, мы можем воспользоваться корнем.

Корень также широко применяется в физике, инженерных расчетах, экономике и других научных и практических областях. Он является неотъемлемой частью математических операций и позволяет нам решать различные задачи, которые возникают в повседневной жизни и профессиональной деятельности.

Различные типы корней

В математике существуют различные типы корней, которые используются для решения уравнений и нахождения значений переменных.

1. Числовой корень — это операция, обратная возведению в степень. Корень из числа a обозначается символом √a и представляет собой число x, такое что x^2 = a. Числовой корень может быть как положительным, так и отрицательным, например, √25 = 5 и √25 = -5.

2. Квадратный корень — это частный случай числового корня, когда a является положительным числом. Квадратный корень из числа a обозначается символом √a и представляет собой положительное число x, такое что x^2 = a. Например, √25 = 5.

3. Кубический корень — это операция, обратная возведению в куб. Кубический корень из числа a обозначается символом ∛a и представляет собой число x, такое что x^3 = a. Кубический корень может быть как положительным, так и отрицательным, например, ∛27 = 3 и ∛27 = -3.

4. Рациональный корень — это корень, который может быть представлен в виде дроби p/q, где p и q — целые числа. Например, √4 = 2/1.

5. Иррациональный корень — это корень, который не может быть представлен в виде рациональной дроби. Например, √2.

6. Комплексный корень — это корень, который содержит мнимую единицу i, так что его невозможно представить в виде действительного числа. Например, √-1 = i.

Знание различных типов корней позволяет более гибко решать уравнения и выполнять различные математические операции.

Как находить корни

Один из основных методов нахождения корней — это метод подстановки. Для этого нужно подставить различные значения вместо переменной в уравнение и проверить, равно ли выражение нулю.

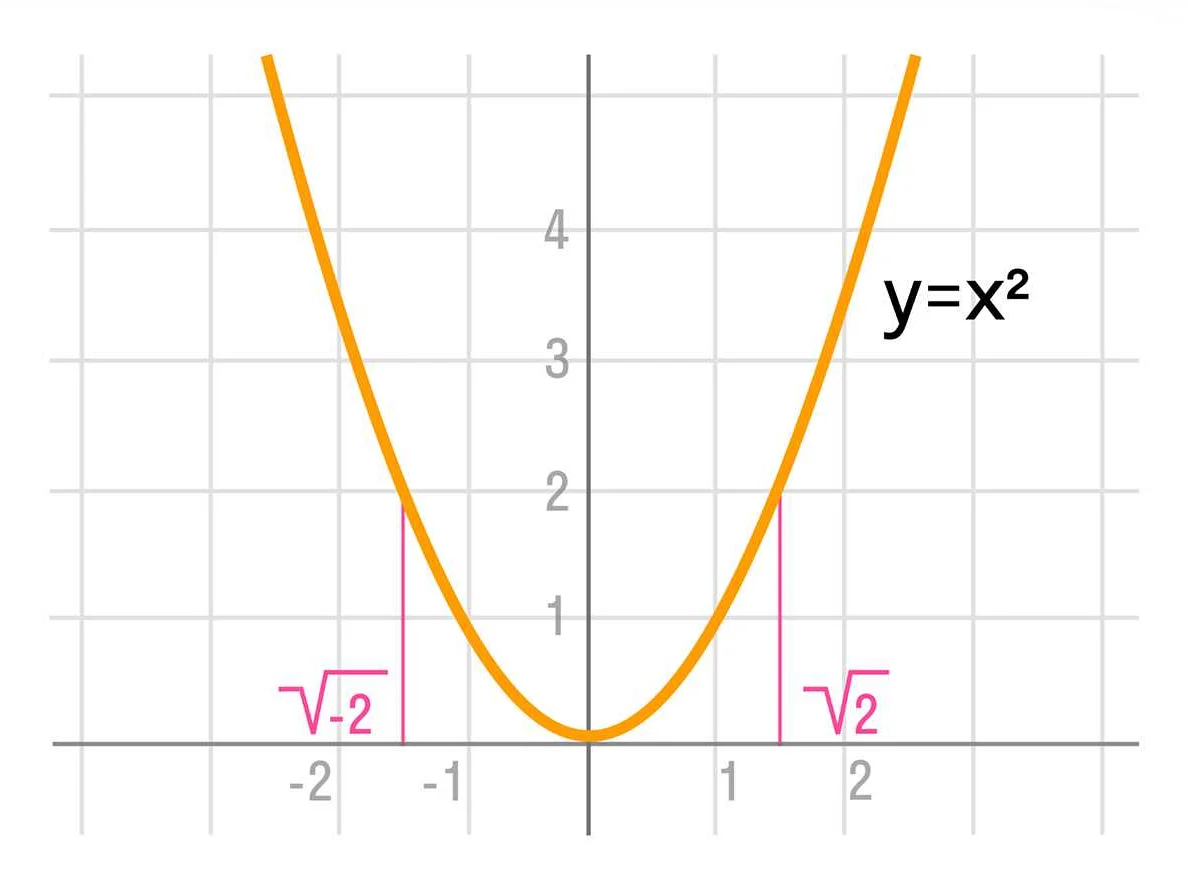
Другой метод — это графический метод. Для построения графика уравнения можно использовать координатную плоскость и отметить точки, в которых значение функции равно нулю. Эти точки будут являться корнями уравнения.

Также существуют специальные формулы для нахождения корней различных типов уравнений, например, квадратных или кубических. Они позволяют найти корни сразу, без необходимости проведения дополнительных вычислений.

Знание и применение этих методов поможет вам находить корни уравнений и решать задачи восьмого класса.

Примеры решения задач с корнями

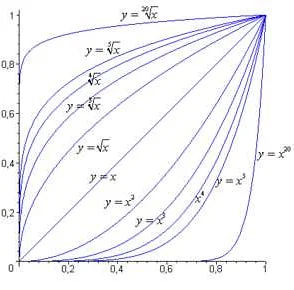
Рассмотрим несколько примеров задач, в которых необходимо решить уравнения с корнями.

Пример 1:

Решите уравнение:

√(x + 3) = 5

Решение:

Возводим обе части уравнения в квадрат:

x + 3 = 25

Вычитаем 3 из обеих частей:

x = 22

Ответ: x = 22.

Пример 2:

Решите уравнение:

√(2x — 1) = √(x + 5)

Решение:

Возводим обе части уравнения в квадрат:

2x — 1 = x + 5

Вычитаем x из обеих частей:

x — 1 = 5

Прибавляем 1 к обеим частям:

x = 6

Ответ: x = 6.

Пример 3:

Решите уравнение:

√(3x + 2) + 2 = 5

Решение:

Вычитаем 2 из обеих частей уравнения:

√(3x + 2) = 3

Возводим обе части уравнения в квадрат:

3x + 2 = 9

Вычитаем 2 из обеих частей:

3x = 7

Делим обе части на 3:

x = 7/3

Ответ: x = 7/3.

Задачи для тренировки на работу с корнями

Задача 1:

Найдите корни уравнения x^2 — 9 = 0.

Решение:

Данное уравнение является квадратным, поэтому можно применить формулу для нахождения корней квадратного уравнения. Формула имеет вид:

x = (-b ± √(b^2 — 4ac)) / 2a

В данном случае, коэффициенты равны:

a = 1, b = 0, c = -9

Подставим значения в формулу:

x = (-0 ± √(0^2 — 4 * 1 * -9)) / (2 * 1)

x = ± √(36) / 2

x = ± 6 / 2

Таким образом, корни уравнения равны:

x = 3

x = -3

Задача 2:

Найдите корни уравнения 2x^2 — 16 = 0.

Решение:

Данное уравнение является квадратным, поэтому можно применить формулу для нахождения корней квадратного уравнения. Формула имеет вид:

x = (-b ± √(b^2 — 4ac)) / 2a

В данном случае, коэффициенты равны:

a = 2, b = 0, c = -16

Подставим значения в формулу:

x = (-0 ± √(0^2 — 4 * 2 * -16)) / (2 * 2)

x = ± √(128) / 4

x = ± 8√2 / 4

x = ± 2√2

Таким образом, корни уравнения равны:

x = 2√2

x = -2√2

Задача 3:

Найдите значение выражения √(5 + √(5 + √(5 + √(5 + √5)))).

Решение:

Данное выражение является итерацией корня. Мы можем продолжать итерацию бесконечно, однако для упрощения вычислений, проведем несколько итераций вручную:

x = √(5 + √(5 + √(5 + √(5 + √5))))

x = √(5 + √(5 + √(5 + √(5 + √5))))

x = √(5 + √(5 + √(5 + √(5 + √5))))

…

Продолжая итерацию, получим:

x ≈ 1,755

Таким образом, значение выражения √(5 + √(5 + √(5 + √(5 + √5)))) примерно равно 1,755.

Свойства корней в математике

1. Произведение корней. Корни можно умножать между собой. Если у нас есть корень числа а и корень числа b, то произведение этих корней равно корню из произведения этих чисел: √(a * b) = √a * √b.
2. Деление корней. Корни можно делить друг на друга. Если у нас есть корень числа а и корень числа b, то отношение этих корней равно корню из отношения этих чисел: √(a / b) = √a / √b.
3. Сложение и вычитание корней. Корни можно складывать и вычитать. Если у нас есть корень числа а и корень числа b, то их сумма будет равна корню из суммы этих чисел: √a + √b. А разность будет равна корню из разности этих чисел: √a — √b.
4. Возведение в степень корня. Если у нас есть корень числа а, то его можно возвести в степень n, где n – натуральное число. В этом случае получится число, которое при возведении в степень n даёт исходное число а: (√a)^n = a.
5. Упрощение корней. Корень можно упрощать. Например, корень из числа 16 можно упростить до 4, так как 4 * 4 = 16. Также можно упрощать корень из рациональных чисел, вынося общий множитель за знак корня.
6. Отрицательный корень. Корень из отрицательного числа не определен в множестве действительных чисел. Однако, его можно определить в множестве комплексных чисел, где √-1 = i.
7. Рациональные и иррациональные корни. Корень называется рациональным, если его можно представить в виде дроби. Иначе он называется иррациональным.

Используя эти свойства, можно с легкостью работать с корнями и решать задачи в математике.

Вопрос-ответ:

Что такое корень в математике?

Корень в математике — это операция, обратная возведению числа в степень. Если число a возвести в степень n и получить число b, то корнем степени n из числа b называется число a. В математической записи корень обозначается символом √.

Как найти корень числа?

Для того чтобы найти корень числа, необходимо взять число, которое нужно извлечь, и указать степень корня. Например, если нужно найти квадратный корень числа 16, то необходимо найти число, которое возводится в квадрат и даёт 16. В данном случае квадратный корень из 16 равен 4, так как 4 * 4 = 16.

Какие бывают виды корней?

В математике существует несколько видов корней. Основными являются квадратный корень, кубический корень и общий корень n-й степени. Квадратный корень из числа a обозначается как √a, кубический корень из числа a обозначается как ∛a, а общий корень из числа a степени n обозначается как √n a.

Какие свойства имеют корни?

У корней имеются несколько свойств. Например, квадратный корень из произведения двух чисел равен произведению квадратных корней этих чисел: √(a * b) = √a * √b. Кроме того, квадратный корень из частного двух чисел равен частному квадратных корней этих чисел: √(a / b) = √a / √b.

Где можно применять знания о корнях в повседневной жизни?

Знание о корнях может быть полезно в различных ситуациях повседневной жизни. Например, при решении задач по финансовому планированию, при расчете длины сторон в геометрии, при анализе данных в статистике и многих других областях. Кроме того, понимание корней помогает лучше понять мир и улучшить логическое мышление.

Практическое применение корней в жизни

Одно из практических применений корней — нахождение квадратного корня числа. Это может быть полезно при решении различных задач, например, при расчете длины стороны квадрата, если известна его площадь. Также квадратные корни используются в физике при решении задач на движение тела и определение его скорости.

Корни также применяются в задачах, связанных с финансами. Например, при расчете процента прибыли или убытка по инвестициям, можно использовать корень, чтобы найти искомый процент. Корни также используются в задачах на проценты по кредитам и вкладам.

Еще одно практическое применение корней — в задачах на геометрию. Корни помогают найти длину сторон треугольника, радиус окружности или длину дуги окружности. Они также используются при рассмотрении задач, связанных с площадью и объемом геометрических фигур.

Корни также находят применение в экономике, при решении задач на расчет суммы процентов, в теории вероятности, при анализе задач на вероятность возникновения событий, и во многих других областях.

Область примененияПримеры использования

Геометрия	Нахождение длины сторон треугольника
Финансы	Расчет процента прибыли по инвестициям
Физика	Определение скорости движения тела
Экономика	Расчет суммы процентов

Видео по теме: