Что такое корень в математике кратко

Корень в математике — это число, которое возводится в квадрат или в другую степень, чтобы получить исходное число. Узнайте, как найти корень, виды корней и их свойства.

Корень — одно из основных понятий в математике, используемое для нахождения числа, которое возводится в некоторую степень, чтобы получить другое число. Корень является обратной операцией к возведению в степень и позволяет найти значение исходного числа.

Определение корня включает в себя две основные компоненты: основание и показатель степени. Основание — это число, из которого берется корень, а показатель степени — это число, указывающее, в какую степень основание будет возведено. Например, корень квадратный из числа 9 равен 3, потому что 3 в квадрате равно 9.

Корни имеют свои основные свойства, которые используются для упрощения вычислений. Некоторые из этих свойств включают в себя:

Свойство корня из произведения: корень из произведения двух чисел равен произведению корней этих чисел. Например, корень квадратный из произведения 4 и 9 равен произведению корней из 4 и 9, то есть 2 и 3, что равно 6.

Свойство корня из частного: корень из частного двух чисел равен частному корней этих чисел. Например, корень квадратный из частного 9 и 4 равен частному корней из 9 и 4, то есть 3 и 2, что равно 1.5.

Свойство корня из степени: корень из числа, возведенного в степень, равен числу, возведенному в эту степень. Например, корень квадратный из числа 16, возведенного в куб, равен 16.

Корни широко применяются в математике и других науках, а также в повседневной жизни. Они используются для решения уравнений, построения графиков функций и нахождения значений величин. Понимание определения и основных свойств корня является важным для успешного изучения и применения математики.

Что такое корень?

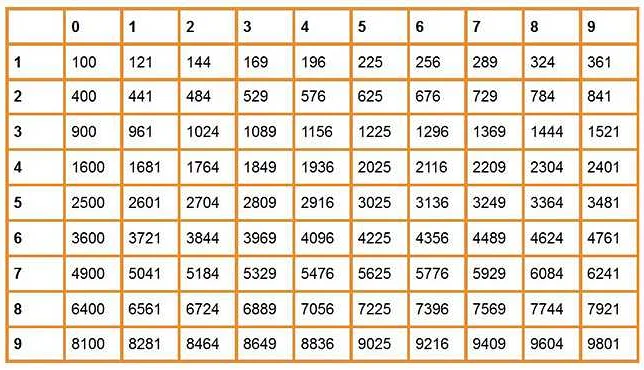
Основные свойства корня:

• Корень из произведения равен произведению корней. √(ab) = √a * √b.
• Корень из частного равен частному корней. √(a/b) = √a / √b.
• Корень из степени равен степени корня. (√a)^n = a^(1/n).
• Корень из корня равен корню из произведения индексов. √(√a) = (√a)^(1/2) = a^(1/4).

Корень используется в различных областях математики и физики, а также в повседневной жизни для решения задач, связанных с извлечением квадратных и других корней.

Какие бывают корни?

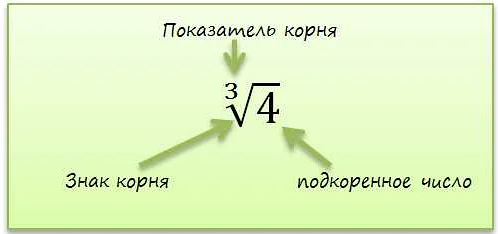
В математике существуют различные типы корней, которые могут быть использованы для решения уравнений и вычисления значений функций. Основные типы корней включают:

• Квадратный корень. Квадратный корень числа — это число, которое при возведении в квадрат даёт исходное число. Например, квадратный корень из 9 равен 3, так как 3 * 3 = 9. Квадратный корень обозначается символом √.
• Кубический корень. Кубический корень числа — это число, которое при возведении в куб даёт исходное число. Например, кубический корень из 8 равен 2, так как 2 * 2 * 2 = 8. Кубический корень обозначается символом √3.
• Корень n-ной степени. Корень n-ной степени числа — это число, которое при возведении в n-ную степень даёт исходное число. Например, корень кубического корня из 27 равен 3, так как 3 * 3 * 3 = 27. Корень n-ной степени обозначается символом √n.

Кроме того, существуют иррациональные корни, которые не могут быть представлены в виде десятичной дроби или конечной десятичной дроби. Например, квадратный корень из 2 является иррациональным числом и не может быть точно представлен в виде десятичной дроби.

Как найти корень?

Одним из наиболее распространенных методов является метод нахождения корня через возведение в степень. Для этого нужно взять исходное число и возвести его в обратную степень. Например, чтобы найти квадратный корень числа 16, нужно возвести его в степень 1/2:

Исходное числоКорень

16	√16 = 161/2 = 4

Еще одним методом нахождения корня является метод итераций. Он основан на последовательном приближении к корню числа путем вычисления среднего арифметического между предыдущим приближением и исходным числом. Например, чтобы найти квадратный корень числа 16 с помощью метода итераций, можно начать с любого числа и последовательно уточнять приближение:

ПриближениеСреднее арифметическое

2	(2 + 16/2) / 2 = 9
9	(9 + 16/9) / 2 ≈ 5.4444
5.4444	(5.4444 + 16/5.4444) / 2 ≈ 4.1364
4.1364	(4.1364 + 16/4.1364) / 2 ≈ 4.0039

Таким образом, последовательно приближаясь к корню, можно получить достаточно точное значение.

Корень как решение уравнения

Корни уравнения могут быть разных типов, в зависимости от вида уравнения. Например, для линейного уравнения вида ax + b = 0, корнем будет значение, при котором левая часть уравнения равна нулю. Таким образом, корень данного уравнения можно найти, решив линейное уравнение и выразив переменную x.

Для квадратного уравнения вида ax^2 + bx + c = 0, существует два типа корней: действительные и комплексные. Действительные корни можно найти, используя формулу дискриминанта, и выражая переменную x. Комплексные корни получаются при решении уравнения с помощью комплексных чисел.

В общем случае, уравнение может иметь разное количество корней. Например, кубическое уравнение может иметь один, два или три корня, в зависимости от его коэффициентов и структуры.

Корни уравнений имеют важное значение в математике и применяются в различных областях. Они позволяют находить значения переменных, при которых уравнения выполняются или функции принимают определенные значения.

Корень как функция

Корень может быть представлен в виде символа √. Например, √a обозначает корень числа a. В данном случае, a является радикандом — числом, из которого извлекается корень.

Основные свойства корня:

1. Корень из положительного числа всегда положительный: √a > 0, где a > 0.
2. Корень из нуля равен нулю: √0 = 0.
3. Корень из отрицательного числа вещественный и не определен в области действительных чисел.
4. Корень из произведения равен произведению корней: √ab = √a ⋅ √b.
5. Корень из частного равен частному корней: √a/b = √a / √b.

Корни широко используются в математике и решении уравнений, а также в других областях, таких как физика и инженерия.

Основные свойства корней

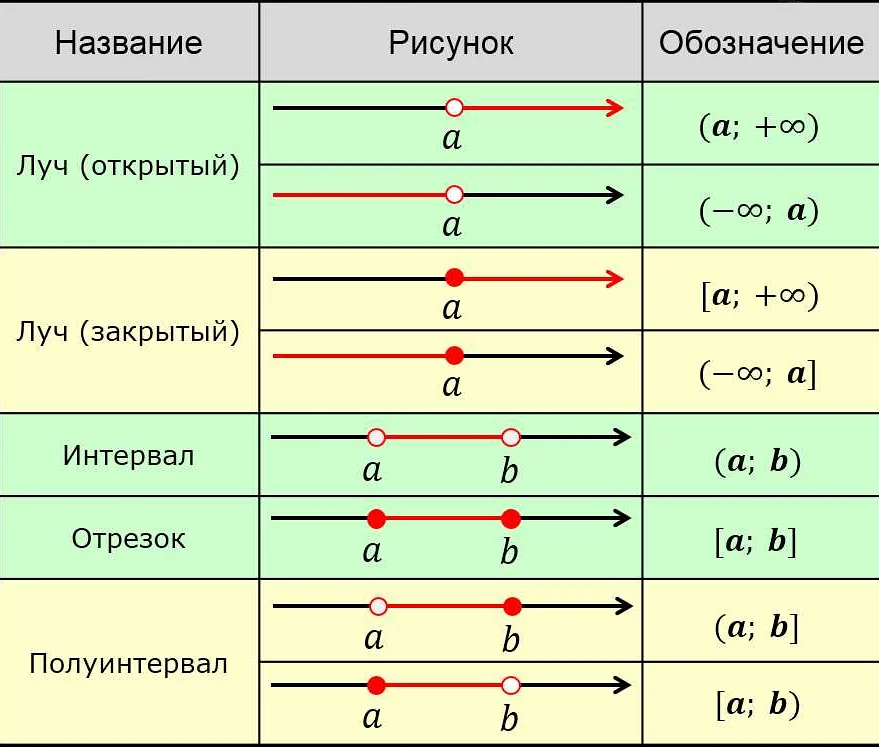
Свойство	Описание
Корень из произведения	Корень из произведения чисел равен произведению корней этих чисел.
Корень из частного	Корень из частного чисел равен частному корней этих чисел.
Корень из суммы	Корень из суммы чисел не всегда равен сумме корней этих чисел.
Корень из разности	Корень из разности чисел не всегда равен разности корней этих чисел.
Корень из корня	Корень из корня числа равен корню из этого числа, умноженному на корень из второго корня.
Корень из нуля	Корень из нуля равен нулю.

Эти свойства корней являются основой для решения уравнений, а также для работы с комплексными числами и другими математическими объектами.

Вопрос-ответ:

Что такое корень в математике?

Корень в математике — это операция, обратная возведению в степень. Если число a является n-ной степенью числа b, то b называют корнем степени n из числа a.

Как записывается корень в математике?

Корень в математике записывается символом √ и числом под ним, которое указывает степень корня. Например, √a означает квадратный корень из числа a.

Какие свойства имеет корень?

Корень обладает несколькими свойствами, включая: свойство извлечения корня из произведения, свойство извлечения корня из частного, свойство извлечения корня из степени и свойство извлечения корня из корня.

Как найти корень числа?

Для нахождения корня числа необходимо использовать специальные математические операции. Например, для нахождения квадратного корня можно использовать функцию sqrt() в программировании или искать числа, возведенные в квадрат, которые приближаются к данному числу.

Какие типы корней существуют?

Существуют различные типы корней, включая квадратный корень, кубический корень, корень четвертой степени и так далее. Квадратный корень из числа a обозначается как √a, кубический корень — ∛a, корень четвертой степени — ∜a и т.д.

Примеры использования корней в математике

Корни широко применяются в математике для решения уравнений и нахождения значений переменных.

Например, при решении квадратного уравнения ax^2 + bx + c = 0 можно использовать формулу дискриминанта:

D = b^2 — 4ac

Если дискриминант равен нулю (D = 0), то у уравнения есть единственный корень, который можно найти по формуле:

x = -b / (2a)

Если дискриминант положителен (D > 0), то у уравнения два различных корня, которые можно найти по формулам:

x_1 = (-b + √D) / (2a)

x_2 = (-b — √D) / (2a)

Если дискриминант отрицателен (D < 0), то у уравнения нет действительных корней.

Корни используются также для вычисления показателей степеней. Например, корень квадратный используется для извлечения квадратного корня из числа. Корень третьей степени используется для извлечения кубического корня. В общем случае, корень степени n используется для извлечения корня n-й степени.

Также корни используются при решении систем уравнений и в других областях математики и естественных наук.

Видео по теме: