Регрессия в математике: понятие, методы и примеры применения

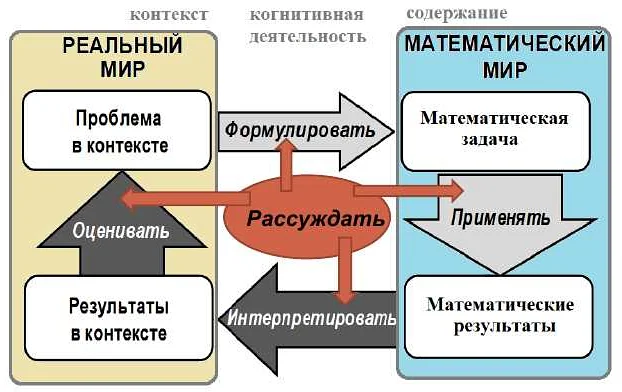
Регрессия – это математический метод, который используется для анализа связи между двумя или более переменными. С его помощью можно предсказать одну переменную, исходя из известных значений других переменных. В статье мы разберем, как работает регрессия и как ее можно применять в реальной жизни.

Регрессия — это важный понятие в математической статистике, которое используется для предсказания зависимости между переменными. Она позволяет нам оценить влияние одной или нескольких переменных на другую и использовать эту информацию для прогнозирования будущих значений.

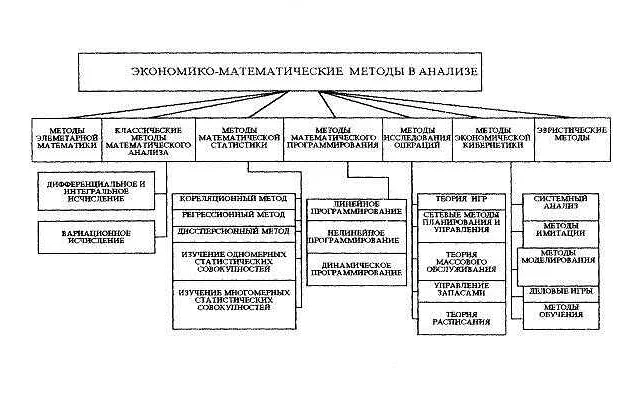
В данной статье мы рассмотрим основные виды регрессии, такие как линейная регрессия, логистическая регрессия, полиномиальная регрессия и другие. Каждый вид регрессии имеет свои особенности и применяется в различных областях, включая экономику, физику, медицину, биологию, социологию и др.

Одной из главных задач регрессии является поиск оптимальной модели, которая максимально точно описывает исходные данные и способна предсказывать будущие значения. Для этого необходимо провести анализ данных, подобрать параметры модели, оценить ее точность и дать интерпретацию результатов.

В настоящее время регрессия широко используется в машинном обучении, где она является одним из основных методов обработки больших объемов данных. Например, регрессионные модели могут быть применены для предсказания цен на акции, расходов на маркетинговые кампании, продажи товаров и услуг, прогнозирования погоды и т.д.

Определение регрессии

Регрессия – это статистический метод, который используется для построения математической модели между двумя или более переменными. Он используется для изучения зависимости между зависимой и независимыми переменными.

Определение регрессии состоит в том, что для предсказания зависимой переменной используются значения независимых переменных. Метод регрессии позволяет исследовать линейную и нелинейную зависимости между переменными, а также оценивать степень влияния каждой из них на зависимую переменную.

Регрессия может использоваться для прогнозирования будущих значений зависимой переменной на основе известных значений независимых переменных. Кроме того, она может использоваться для определения возможных причин изменения зависимой переменной в прошлом.

Все виды регрессии имеют общую цель – предсказать значения зависимой переменной на основе значений независимых переменных. Но каждый вид регрессии имеет свои характеристики, ограничения и применения в реальной жизни.

Общие виды регрессии

Линейная регрессия является наиболее распространенным и простым видом регрессии. Она используется для описания линейных зависимостей между переменными. Это означает, что модель просто находит линию, которая наилучшим образом подходит для подгонки данных.

Нелинейная регрессия используется для моделирования сложных нелинейных зависимостей между переменными. Это может быть любая кривая, не только линия. Например, квадратичная, экспоненциальная или логарифмическая кривые могут быть использованы в качестве нелинейной модели.

Логистическая регрессия используется, когда необходимо предсказать вероятность бинарного события, например, прохождение экзамена или отказ от кредита. В этой модели используется логистическая функция для описания взаимосвязи между переменными и вероятностью события.

Множественная линейная регрессия используется, когда нужно описать зависимость между более чем двумя переменными. Эта модель может быть полезна, когда нужно учитывать множество факторов при прогнозировании результатов.

Полиномиальная регрессия используется, когда нужно использовать полиномы для описания зависимости между переменными. Это может быть — кривая второго порядка, третьего порядка или любой другой порядок. Эта модель часто используется для анализа экспериментальных данных.

В зависимости от поставленных задач и данных, можно выбрать наиболее подходящий тип регрессии.

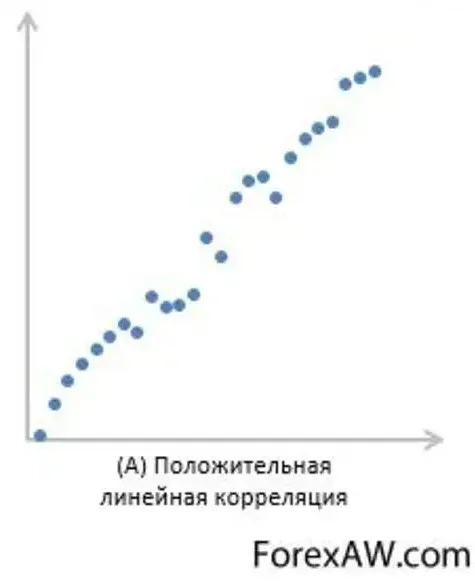
Простая линейная регрессия

Простая линейная регрессия – это модель, которая ищет зависимость одной переменной (независимой) от другой переменной (зависимой) с помощью прямой линии. В этой модели предполагается, что зависимая переменная изменяется пропорционально независимой переменной.

Простая линейная регрессия часто используется для прогнозирования значения переменной на основе ее значения в прошлом. В этом случае независимая переменная используется для прогнозирования зависимой переменной. Например, можно использовать простую линейную регрессию для прогнозирования продаж магазина на основе времени года или для прогнозирования цены на недвижимость на основе площади квартиры.

Простая линейная регрессия основывается на методе наименьших квадратов. Этот метод находит линию, которая минимизирует сумму квадратов отклонений между наблюдаемыми значениями зависимой переменной и значениями, предсказанными моделью. Чем меньше значение суммы квадратов отклонений, тем лучше соответствие модели и наблюдаемых данных.

Для применения простой линейной регрессии необходимы наблюдения по зависимой и независимой переменным. Из этих наблюдений можно получить уравнение линии, которое может быть использовано для прогнозирования зависимой переменной в будущем.

Множественная линейная регрессия

Множественная линейная регрессия используется для анализа взаимосвязи между зависимой переменной и двумя или более независимыми переменными. Она представляет собой расширение простой линейной регрессии, где есть только одна независимая переменная.

Для множественной линейной регрессии необходимо задать модель, которая будет являться линейным комбинацией предикторов. Коэффициенты этой модели, называемые коэффициентами регрессии, определяют влияние каждой независимой переменной на зависимую переменную.

Одним из основных методов для оценки коэффициентов регрессии является метод наименьших квадратов (OLS). Этот метод находит наилучшую линейную комбинацию предикторов через минимизацию суммы квадратов отклонений между наблюдаемыми значениями зависимой переменной и предсказанными значениями, полученными с помощью модели.

Множественная линейная регрессия широко используется в таких областях, как экономика, социология, медицина, бизнес-анализ и другие, где нужно понять зависимость между несколькими переменными для принятия решений. Она может помочь выявить факторы, оказывающие наибольшее влияние на зависимую переменную, и предсказать значения зависимой переменной на основе значений независимых переменных.

Логистическая регрессия

Логистическая регрессия — это метод статистического анализа, который используется для предсказания вероятности возникновения двоичного события, такого как «да» или «нет», «правильный» или «неправильный». Она используется для определения связи между зависимыми и независимыми переменными и для построения математических моделей, которые могут быть использованы для прогнозирования вероятности возникновения события.

Основная задача логистической регрессии состоит в нахождении функции, которая наилучшим образом соответствует данным. Это достигается путем определения коэффициентов регрессии, которые связывают предикторы (независимые переменные) с откликом (зависимой переменной).

Для непрерывных переменных логистическая регрессия использует логистическую функцию, которая превращает исходный диапазон значений в диапазон значений от 0 до 1. Эта функция позволяет использовать значение вероятности в качестве вывода и для классификации данных в две категории.

Логистическая регрессия — это мощный инструмент для анализа данных, который широко используется в многих отраслях, включая маркетинг, медицину, финансы и т.д. Он может помочь выявить ключевые факторы, которые влияют на определенные результаты, и прогнозировать вероятность будущих событий.

Важно отметить, что логистическая регрессия не является универсальным методом предсказания и не подходит для всех типов данных. Она лучше всего работает с двоичными данными и может давать ложные результаты, если использовать ее для анализа данных, которые не соответствуют ее ограничениям.

Практическое применение регрессии

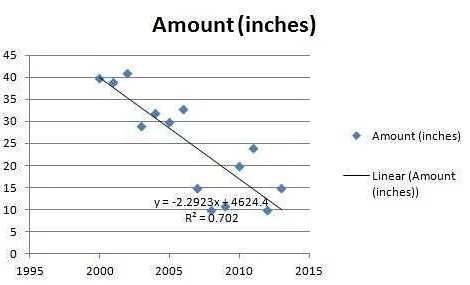
Регрессия — это мощный инструмент статистического анализа, который активно используется в многих областях науки и бизнеса для прогнозирования будущих значений на основе исторических данных. Рассмотрим несколько примеров практического применения регрессии.

В бизнесе регрессия может помочь оптимизировать производственные процессы и улучшить качество продукции. Например, построение модели регрессии на основе производственных данных может помочь в определении оптимальных условий работы оборудования и выявлении факторов, влияющих на качество продукции.

В маркетинге регрессия может использоваться для прогнозирования продаж на основе исторических данных и определения показателей эффективности рекламных кампаний. Анализ регрессии может также помочь в принятии решений о ценообразовании на основе оценки влияния различных факторов на спрос на продукцию.

В медицине регрессия может использоваться для прогнозирования риска развития заболеваний на основе исторических данных, а также для оценки эффективности медицинских процедур. Например, модель регрессии может помочь в определении наиболее эффективного лечения определенного заболевания на основе медицинских данных.

Таким образом, регрессия представляет собой мощный инструмент, который может помочь в принятии решений и оптимизации бизнес-процессов в различных областях деятельности. Важно понимать, что для построения модели регрессии необходимы качественные данные и достаточный объем информации для анализа.

Применение регрессии в экономике

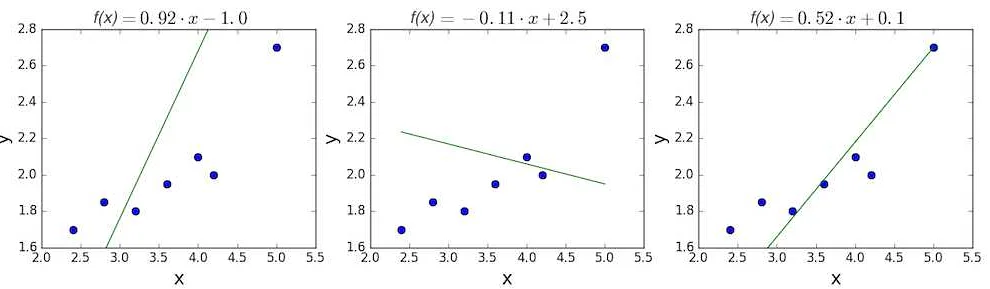
Регрессия в экономике применяется для определения связи между экономическими показателями. С ее помощью можно построить модели, которые позволяют оценить, как один показатель влияет на другой.

Например, можно использовать регрессионный анализ, чтобы определить зависимость между объемом продаж и рекламными затратами. На основе данных о продажах и затратах можно вычислить коэффициент корреляции и установить, насколько сильна связь между этими двумя показателями.

Кроме того, регрессия может использоваться для прогнозирования будущих значений экономических показателей. На основе имеющихся данных можно построить модель и использовать ее для того, чтобы спрогнозировать, как изменится значение данного показателя в будущем при изменении других факторов.

В экономике регрессионный анализ может применяться для многих целей, включая бюджетное планирование, определение стоимости товаров и услуг, анализ экономических трендов и принятие инвестиционных решений.

Применение регрессии в медицине

Регрессионный анализ является важным инструментом в медицине для прогнозирования и предсказания различных факторов, таких как возраст, рост, вес и уровень гормонов в крови. Он используется для исследования связи между различными переменными в медицинских исследованиях.

Например, применение регрессии в медицине может помочь в определении возможных факторов риска для болезней, таких как диабет, сердечно-сосудистые заболевания и рак. При использовании регрессионного анализа, медицинские исследователи могут выявить связь между такими факторами как табакокурение, испытуемый возраст и повышенный уровень холестерина, и риск развития определенного заболевания.

Также регрессионный анализ используется в медицине для прогнозирования будущих исходов лечения пациентов. С помощью регрессионного анализа можно определить, какие факторы, такие как генетический фон, тип заболевания и уровень тяжести, могут оказать влияние на результаты лечения. Это может помочь врачам и медицинским работникам принимать более информированные решения о лечении и управлении заболеванием в будущем.

В целом, регрессионный анализ является важным и мощным инструментом для медицинских исследований. Он может быть использован для выявления факторов риска, прогнозирования исходов лечения и определения различий между пациентами с разными заболеваниями или разными уровнями тяжести заболевания.

Применение регрессии в маркетинге

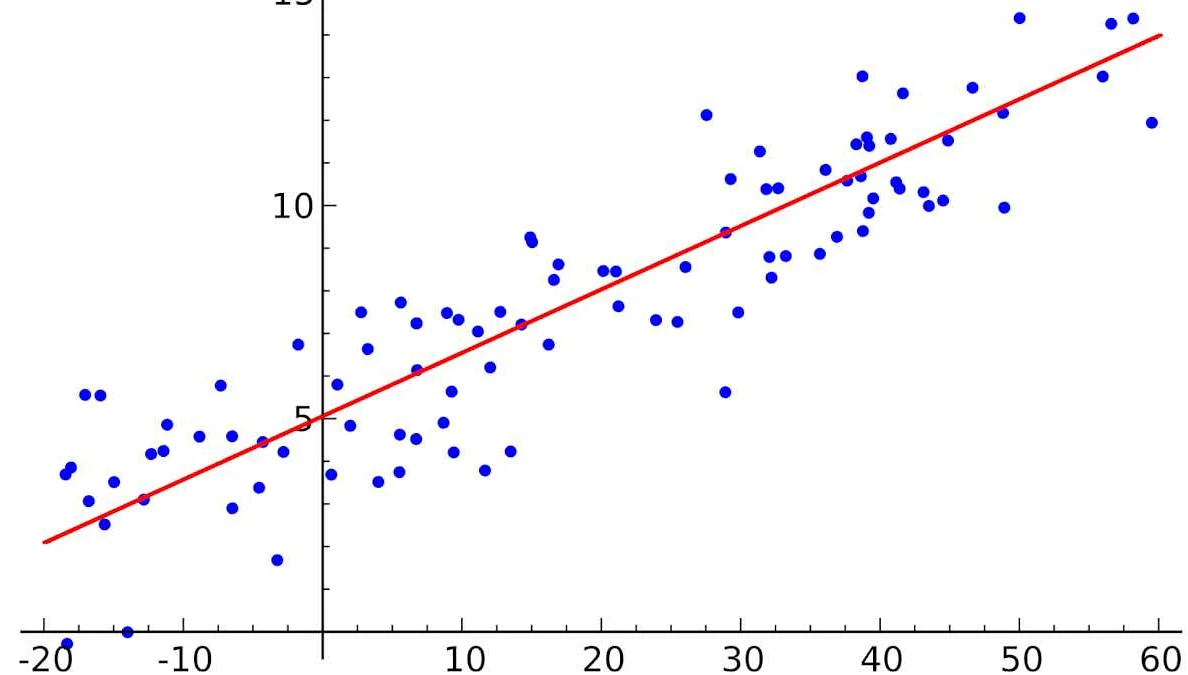
Регрессионный анализ — это мощный инструмент для прогнозирования поведения покупателей и определения того, какие факторы влияют на показатели продаж. Это позволяет маркетологам принимать более уверенные решения и сокращать затраты на маркетинговые кампании.

С помощью регрессионного анализа маркетологи могут определить влияние различных факторов на продажи, таких как цена товара, рекламные затраты, местоположение магазина, возраст целевой аудитории и т.д. Более того, регрессионный анализ помогает маркетологам понимать, как эти факторы влияют на показатели продаж в зависимости от времени года, дня недели или даже времени суток.

Например, если маркетолог хочет узнать, какие факторы влияют на продажи в праздничный сезон, он может использовать регрессионный анализ для определения уровня важности таких факторов, как праздничные скидки, рекламные кампании и количество посетителей в магазинах.

Кроме того, с помощью регрессионного анализа маркетологи могут создавать прогнозы продаж, оценивать эффективность маркетинговых кампаний и улучшать маркетинговые стратегии в целом. Например, прогнозируя продажи с помощью регрессионного анализа, маркетолог может планировать свой бюджет и ресурсы на основе предполагаемых доходов в будущем.

Таким образом, регрессионный анализ является ценным инструментом для маркетологов, помогающим им определить, какие факторы влияют на продажи и как изменения в этих факторах могут повлиять на будущие показатели продаж. Это позволяет маркетологам принимать более обоснованные решения и улучшать маркетинговые стратегии для более эффективного продвижения продуктов и услуг.

Применение регрессии в науке и исследованиях

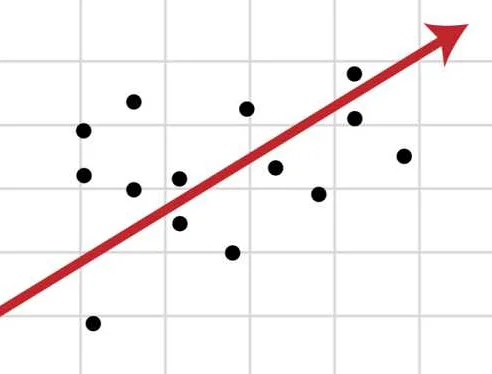
Регрессия является мощным инструментом для анализа данных в науке и исследованиях. Во многих областях знания, включая природные, социологические и медицинские науки, регрессионный анализ используется для изучения взаимосвязи между переменными.

В биологии, регрессия может использоваться для изучения влияния различных факторов на изменения в популяциях животных и растений. Например, исследования могут показать, как изменение температуры влияет на рост и размножение растений.

В социологии, регрессионный анализ может использоваться для изучения взаимосвязей между социально-экономическим положением и здоровьем. Например, исследования могут определить, какие факторы связаны с более высокими показателями заболеваемости раком у людей с низким доходом.

• Регрессия также может быть использована в:
• Экономике для изучения взаимосвязи между различными факторами, влияющими на отрасль;
• Политических науках, чтобы понять, как различные факторы влияют на голосование;
• Психологии, чтобы изучить взаимосвязь между различными факторами и поведением людей.

Регрессионный анализ может помочь ученым понять, как различные факторы взаимодействуют между собой и как они влияют на конечный результат. Это может привести к разработке более эффективных стратегий и политик во многих областях, включая экономику, социальные услуги, здравоохранение, окружающую среду и технологии.

Вопрос-ответ:

Что такое регрессия в математике?

Регрессия в математике представляет собой статистический метод, используемый для анализа отношений и зависимостей между различными переменными. Она помогает определить связь между одной или несколькими независимыми переменными и зависимой переменной.

Какие основные виды регрессионного анализа существуют?

Существует несколько видов регрессионного анализа: простая линейная регрессия, множественная линейная регрессия, показательная регрессия, полиномиальная регрессия и т.д. Каждый из них применяется в зависимости от того, какие данные нужно анализировать и какую зависимость нужно исследовать.

Как применяются результаты регрессионного анализа в практической работе?

Регрессионный анализ находит свое применение в различных областях, включая маркетинг, финансы, экономику, психологию, медицину и т.д. Результаты регрессионного анализа могут использоваться для прогнозирования будущих социальных или экономических тенденций, а также для принятия эффективных решений в бизнесе и других областях.

Что такое коэффициент детерминации?

Коэффициент детерминации представляет собой меру того, насколько хорошо уравнение регрессии соответствует реальным данным. Он принимает значения от 0 до 1, где 0 означает отсутствие зависимости, а 1 — идеальное соответствие. Чем ближе значение коэффициента детерминации к 1, тем точнее уравнение регрессии.

Как проводится простая линейная регрессия?

Простая линейная регрессия проводится путем построения уравнения прямой линии, которая наилучшим образом отображает зависимость между одной независимой переменной и зависимой переменной. Для этого необходимо найти угловой коэффициент (наклон) и точку пересечения с осью ординат (свободный член) этой линии.

В чем отличие множественной линейной регрессии от простой?

Множественная линейная регрессия является расширенной версией простой линейной регрессии, где вместо одной независимой переменной рассматривается несколько. Это позволяет учесть большее количество факторов, влияющих на зависимую переменную, и более точно определить их влияние. Однако, при использовании множественной регрессии увеличивается сложность анализа и требуются более продвинутые статистические методы.

Какие недостатки может иметь регрессионный анализ?

Регрессионный анализ имеет ряд недостатков, включая ограниченность данных, нелинейность связей между переменными, неучтенность скрытых факторов, ошибки в данных и т.д. Кроме того, результаты регрессионного анализа могут быть истолкованы неверно, если не учитывать особенности конкретных данных и контекста, в котором проводится анализ.

Регрессионный анализ: плюсы и минусы

Плюсы:

1. Позволяет установить, есть ли зависимость между переменными и каков ее характер;
2. Дает возможность понять, как каждая переменная влияет на объясняемую переменную;
3. Позволяет спрогнозировать значения переменной, основываясь на имеющихся данных;
4. Хорошо подходит для анализа данных в экономике, финансах, маркетинге и других областях.

Минусы:

• Необходимость выборки достаточного объема и качества;
• При наличии корреляции между независимыми переменными возможно смещение оценок коэффициентов;
• При наличии выбросов или выбивающихся значений результаты могут быть ненадежными;
• Не всегда возможно установить причинно-следственную связь между переменными.

В целом, регрессионный анализ является важным инструментом для анализа данных и прогнозирования будущих значений. Однако, чтобы получить достоверные результаты, необходимо учитывать его ограничения и использовать его в сочетании с другими методами статистического анализа.

Видео по теме: