Что такое матрица в математике
Содержимое
- 1 Что такое матрица в математике
- 1.1 Матрица в математике: общее определение
- 1.2 Матрица как система упорядоченных элементов
- 1.3 Матрица как способ представления данных
- 1.4 Матрица в линейной алгебре: основные понятия
- 1.5 Операции над матрицами: сложение, умножение и др.
- 1.6 Матрица как инструмент для решения систем уравнений
- 1.7 Применение матриц в различных областях науки и техники
- 1.8 Вопрос-ответ:
- 1.9 Видео по теме:
Матрица в математике – это упорядоченный набор чисел, расположенных в виде прямоугольной таблицы. В статье рассматривается определение матрицы, ее свойства и основные операции. Вы узнаете, как умножать матрицы, находить их определители и обратные матрицы. Также рассматривается практическое применение матриц в различных областях науки и техники.
Матрица – это математический объект, который представляет собой прямоугольную таблицу чисел или символов. Матрицы широко используются в различных областях математики, физики, экономики и компьютерных наук. Они являются одним из основных инструментов линейной алгебры.
Матрица состоит из элементов, которые расположены в виде строк и столбцов. Каждый элемент матрицы имеет свои координаты – номер строки и номер столбца. Обычно элементы матрицы обозначаются символами aij, где i – номер строки, j – номер столбца.
Матрицы можно складывать, вычитать, умножать на число и другую матрицу. Одно из основных свойств матрицы – ассоциативность умножения, то есть (AB)C = A(BC). Также матрицы могут быть транспонированы, то есть строки матрицы становятся столбцами, а столбцы – строками.
Матрицы играют важную роль в решении систем линейных уравнений, преобразовании геометрических фигур и в других областях математики. Они также используются в компьютерной графике, обработке изображений и анализе данных.
Матрица в математике: общее определение
Матрицу обычно обозначают заглавными латинскими буквами, например, A, B, C, а ее элементы обозначают малыми латинскими буквами, с индексами, указывающими их положение в матрице. Например, aij обозначает элемент, расположенный в i-й строке и j-м столбце матрицы A.
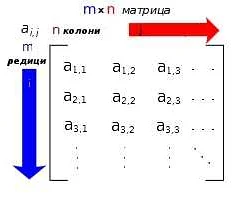
Размеры (или порядок) матрицы определяются количеством строк и столбцов. Если матрица имеет m строк и n столбцов, ее размеры обозначаются m x n или просто m:n.
Матрицы могут быть различных типов, включая квадратные, прямоугольные, нулевые, единичные, симметричные и другие. Кроме того, с матрицами можно выполнять различные операции, такие как сложение, вычитание, умножение на число, умножение матриц и транспонирование.
Общее определение матрицы в математике позволяет использовать их для моделирования и решения различных задач, а также для представления различных данных и информации в удобной форме.
Матрица как система упорядоченных элементов
Матрица в математике представляет собой упорядоченную таблицу из чисел или символов, расположенных в определенном порядке. Она представляет собой систему элементов, которые могут быть числами, переменными или функциями.
Каждый элемент матрицы находится в определенной позиции, которая определяется номером строки и столбца. Поэтому матрица содержит информацию о своих размерах — количество строк и столбцов.
Матрицы широко используются в математике, физике, экономике, информатике и других областях для решения различных задач. Они позволяют удобно описывать и решать системы линейных уравнений, выполнять операции с векторами, моделировать и анализировать сложные системы и многое другое.
Матрица представляется в виде прямоугольной таблицы, где каждый элемент занимает свою ячейку. Строки и столбцы матрицы нумеруются, начиная с 1. Например, элемент матрицы А, находящийся в i-й строке и j-м столбце, обозначается Аij.
Матрицы могут быть различных типов: квадратные, прямоугольные, диагональные, верхнетреугольные, нижнетреугольные и другие. Основные операции, которые можно выполнять с матрицами, включают сложение, умножение на число, умножение матрицы на матрицу и транспонирование.
Таким образом, матрица представляет собой удобное и эффективное математическое средство для описания и решения различных задач, которые возникают в различных областях науки и техники.
Матрица как способ представления данных
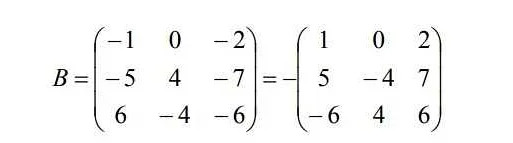
Использование матрицы для представления данных позволяет упорядочить информацию и организовать ее в структурированном виде. Это особенно полезно, когда имеется большой объем информации или когда она имеет сложную структуру.
Матрицы широко применяются в различных областях, включая математику, физику, экономику, информатику и другие науки. Например, в линейной алгебре матрицы используются для решения систем линейных уравнений и для описания преобразований векторов. В экономике матрицы могут использоваться для моделирования экономических процессов и анализа взаимосвязей между различными переменными.
Кроме того, матрицы могут быть использованы для представления графической информации, такой как изображения и видео. В этом случае каждый элемент матрицы может представлять яркость пикселя или цветовую компоненту.
Матрица также может быть использована для хранения и обработки данных в компьютерных программах. Например, в языке программирования Python матрицы могут быть представлены с помощью специальных структур данных, таких как списки или массивы.
Таким образом, матрица является эффективным и универсальным способом представления данных. Она позволяет организовать информацию и обеспечить доступ к ней для различных целей, таких как анализ, моделирование и обработка данных.
Матрица в линейной алгебре: основные понятия
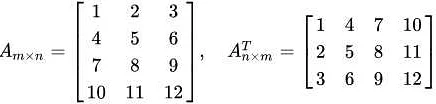
Основные понятия, связанные с матрицами, включают следующее:
- Размерность матрицы – это количество строк и столбцов в матрице. Матрицы обозначаются символами заглавных латинских букв, например, A, B, C и т.д.
- Элементы матрицы – это числа или символы, расположенные внутри матрицы. Каждый элемент матрицы обозначается индексами i и j, где i – номер строки, а j – номер столбца. Например, элемент матрицы A, находящийся в i-й строке и j-м столбце, обозначается как Aij.
- Главная диагональ – это линия элементов матрицы, расположенных от верхнего левого угла до нижнего правого угла. Элементы главной диагонали обозначаются как Aii.
- Нулевая матрица – это матрица, в которой все элементы равны нулю.
- Единичная матрица – это квадратная матрица, у которой на главной диагонали стоят единицы, а остальные элементы равны нулю.
- Транспонированная матрица – это матрица, полученная из исходной матрицы путем замены строк на столбцы и столбцов на строки.
- Определитель матрицы – это число, которое можно вычислить для квадратной матрицы и которое используется для решения линейных систем уравнений и других задач.
Понимание основных понятий и свойств матриц является важной основой для изучения линейной алгебры и ее применения в различных областях науки и техники.
Операции над матрицами: сложение, умножение и др.
Одной из основных операций над матрицами является сложение. Сложение матриц проводится путем покомпонентного сложения соответствующих элементов матриц. Для сложения двух матриц необходимо, чтобы они имели одинаковое количество строк и столбцов.
Если даны две матрицы A и B размерности m x n, то результатом сложения будет матрица C, также размерности m x n, где каждый элемент с индексом (i, j) равен сумме соответствующих элементов матриц A и B с индексом (i, j).
Другой важной операцией над матрицами является умножение. Умножение матриц проводится путем комбинирования элементов матрицы-множителя и матрицы-множителя. При этом число столбцов матрицы-множителя должно быть равно числу строк матрицы-множителя.
Если даны две матрицы A и B размерности m x n и n x p, то результатом умножения будет матрица C размерности m x p, где каждый элемент с индексом (i, j) равен сумме произведений соответствующих элементов i-й строки матрицы A и j-го столбца матрицы B.
Кроме сложения и умножения, существуют и другие операции над матрицами, такие как вычитание, умножение на скаляр, транспонирование и др. Эти операции позволяют выполнять различные преобразования с матрицами и решать различные задачи в математике, физике, экономике и других областях.
Матрица как инструмент для решения систем уравнений
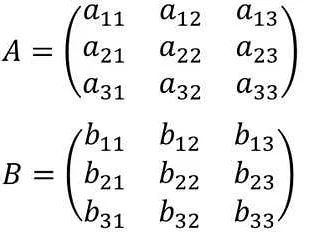
Системы уравнений — это набор уравнений, которые должны быть решены одновременно. Они возникают в различных областях науки и техники и могут иметь разное количество неизвестных. Каждая система уравнений представляется в матричной форме, где коэффициенты уравнений и переменные объединяются в матрицу.
Матрица системы уравнений состоит из строк и столбцов, где каждая строка соответствует одному уравнению, а каждый столбец — одной переменной. Коэффициенты перед переменными записываются в ячейки матрицы.
Для решения системы уравнений с помощью матриц используется метод Гаусса, который основан на элементарных преобразованиях над матрицей. Элементарные преобразования включают в себя перестановку строк, умножение строки на число и сложение строк. Цель метода Гаусса — привести матрицу системы уравнений к упрощенному виду.
После приведения матрицы к упрощенному виду можно решить систему уравнений. Если в упрощенной матрице есть строка, где все элементы равны нулю, и соответствующий элемент вектора свободных членов не равен нулю, то система уравнений не имеет решения. Если же все строки упрощенной матрицы состоят из нулей, кроме одной строки, где все элементы равны нулю, и соответствующий элемент вектора свободных членов также равен нулю, то система уравнений имеет бесконечное количество решений.
Решение системы уравнений с помощью матриц позволяет упростить и автоматизировать процесс решения, особенно в случае большого количества уравнений и неизвестных. Это делает матрицы очень полезными инструментами для работы с системами уравнений в математике и научных исследованиях.
Применение матриц в различных областях науки и техники
1. Анализ данных и статистика: Матрицы используются для хранения и обработки больших объемов данных. Они позволяют эффективно организовывать информацию и выполнять различные операции, такие как умножение, сложение и нахождение обратной матрицы. В статистике матрицы применяются для моделирования случайных процессов и анализа данных.
2. Линейная алгебра: Матрицы используются для решения систем линейных уравнений, нахождения собственных значений и векторов, а также для решения задач линейного программирования. Линейная алгебра является основой для многих других областей математики и науки.
3. Компьютерная графика: Матрицы используются для преобразования и отображения графических объектов на экране. Они позволяют выполнять операции масштабирования, поворота, сдвига и проекции объектов на двумерную или трехмерную плоскость.
4. Криптография: Матрицы используются для шифрования и дешифрования информации. Они позволяют обеспечить безопасность передаваемых данных путем применения различных математических операций к матрицам.
5. Машинное обучение и искусственный интеллект: Матрицы используются для хранения и обработки данных в алгоритмах машинного обучения. Они позволяют анализировать большие объемы информации и находить закономерности, что позволяет создавать эффективные модели и предсказывать результаты.
6. Физика и инженерия: Матрицы применяются для описания физических систем и решения уравнений движения. Они используются при моделировании электрических схем, механических конструкций и других сложных систем.
Это только некоторые примеры применения матриц в различных областях науки и техники. Все больше и больше областей находят применение для матриц, благодаря их универсальности и эффективности в обработке данных и моделировании сложных систем.
Вопрос-ответ:
Что такое матрица в математике?
Матрица в математике — это упорядоченный набор чисел, расположенных в виде прямоугольной схемы. Она состоит из m строк и n столбцов, где каждый элемент обозначается aij, где i — номер строки, j — номер столбца.
Какие свойства имеют матрицы?
Матрицы обладают рядом свойств, среди которых: сложение и вычитание матриц, умножение матрицы на скаляр, умножение матрицы на матрицу, транспонирование матрицы, нахождение определителя и обратной матрицы.
Как выполняются операции сложения и вычитания матриц?
Операции сложения и вычитания матриц выполняются покомпонентно. Для сложения матрицы A и матрицы B необходимо сложить соответствующие элементы: (Aij + Bij). Для вычитания матрицы B из матрицы A нужно вычесть соответствующие элементы: (Aij — Bij).
Что такое транспонирование матрицы?
Транспонирование матрицы — это операция, при которой строки и столбцы меняются местами. Если исходная матрица имеет размерность m x n, то после транспонирования она становится матрицей размерности n x m. Элементы новой матрицы обозначаются aji (ранее aij).
Что такое определитель матрицы и как его найти?
Определитель матрицы — это число, которое вычисляется для квадратной матрицы и позволяет определить ее свойства. Определитель матрицы обозначается det(A) или |A|. Его можно найти различными способами, например, с помощью разложения по строке или столбцу, с использованием свойств определителя или с помощью формулы для матрицы 2×2.
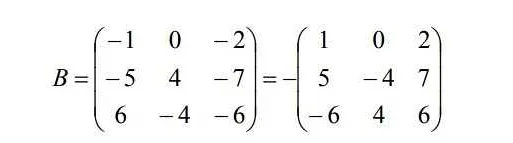


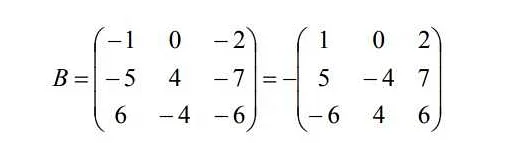
Матрица – это мощный инструмент, который используется в математике и других науках. Она представляет собой упорядоченный набор чисел, разделенных на строки и столбцы. Матрицы могут быть разных размеров и содержать разные элементы: числа, переменные или даже функции. Одно из главных свойств матрицы – ее возможность участвовать в арифметических операциях. Сложение, вычитание, умножение – все это можно делать с матрицами. Однако, есть некоторые правила, которые нужно соблюдать при выполнении этих операций. Матрицы также позволяют решать системы уравнений и находить собственные значения и собственные векторы. Они имеют широкое применение в физике, экономике, компьютерной графике и других областях. Понимание матрицы – важный навык для любого, кто интересуется математикой и наукой в целом. Используя матрицы, мы можем моделировать сложные системы и анализировать данные. Поэтому, если вы хотите глубже погрузиться в мир математики, необходимо освоить основы работы с матрицами.
Статья очень понятно объясняет, что такое матрица в математике. Я всегда задавалась вопросом, для чего она используется, и наконец-то нашла ответ. Очень интересно, что матрица представляет собой таблицу чисел, которая имеет много применений в разных областях науки и техники. Особенно мне понравилось, что матрица может использоваться для решения систем линейных уравнений. Это действительно помогает сократить время и упростить вычисления. Теперь я полностью понимаю, что такое матрица и как ее использовать. Большое спасибо за информативную и понятную статью!