Что называют матрицей математика
Содержимое
Матрица в математике представляет собой упорядоченный набор чисел, расположенных в виде прямоугольной таблицы. Она используется для решения систем линейных уравнений, а также для описания и анализа различных математических структур и операций. Узнайте больше о понятии матрицы и ее применении в математике на нашем сайте.
Матрица – это одна из основных математических структур, используемых для анализа и решения различных задач. Она представляет собой упорядоченный набор чисел, расположенных в виде прямоугольной таблицы. Каждое число в матрице называется элементом. В матрице также определено количество строк и столбцов, которые образуют ее размерность. Количество строк и столбцов называется порядком матрицы.
Матрицы широко применяются в различных областях науки и техники, таких как физика, экономика, информатика и другие. Они позволяют компактно и удобно описывать системы линейных уравнений, проводить операции с векторами и выполнять множество других операций. Кроме этого, матрицы играют важную роль в линейной алгебре, которая является одной из основных разделов математики.
Важно отметить, что матрицы имеют множество свойств и операций, которые позволяют эффективно работать с ними. Например, матрицы можно складывать, вычитать, умножать на число и друг друга, а также находить их определители и обратные матрицы. Кроме того, матрицы могут быть классифицированы по различным признакам, таким как симметричность, диагональность и другие.
Использование матриц в математике дает возможность решать сложные задачи, связанные с линейными системами, преобразованиями координат и многими другими. Изучение матриц является важным шагом в понимании и применении линейной алгебры и подготавливает студентов к решению более сложных математических задач.
Что такое матрица в математике?

Матрицы широко используются в математике, физике, экономике, информатике и других науках для описания и решения различных задач. Они являются удобным инструментом для организации и обработки данных.
Матрицы могут быть разных размеров: квадратные (количество строк равно количеству столбцов), прямоугольные (количество строк не равно количеству столбцов) и вырожденные (содержат нулевые строки или столбцы).
Матрицы могут быть складываться, вычитаться и умножаться на число. Операции над матрицами позволяют решать системы линейных уравнений, находить обратные матрицы, вычислять определители и многое другое.
В матрице элементы обычно обозначаются строчными латинскими буквами, а размерность матрицы указывается верхним индексом.
Основные определения
Размерностью матрицы называется количество строк и столбцов, обозначаемых соответственно буквами m и n. Матрица размерности m x n имеет m строк и n столбцов.
Элемент матрицы обозначается символом aij, где i — номер строки, а j — номер столбца, в котором находится элемент.
Главной диагональю матрицы называется линия, составленная из элементов, расположенных на пересечении строки и столбца с одинаковыми номерами. Элементы главной диагонали обозначаются как a11, a22, …, ann.
Единичной матрицей называется квадратная матрица, у которой на главной диагонали стоят единицы, а все остальные элементы равны нулю.
Нулевой матрицей называется матрица, все элементы которой равны нулю.
Квадратной матрицей называется матрица, у которой число строк равно числу столбцов.
Транспонированной матрицей называется матрица, полученная из исходной матрицы путем замены строк на столбцы и столбцов на строки.
Симметричной матрицей называется квадратная матрица, которая равна своей транспонированной матрице.
Диагональной матрицей называется квадратная матрица, у которой все элементы, кроме элементов главной диагонали, равны нулю.
Треугольной матрицей называется квадратная матрица, у которой все элементы, находящиеся выше главной диагонали или ниже главной диагонали, равны нулю.
Структура матрицы
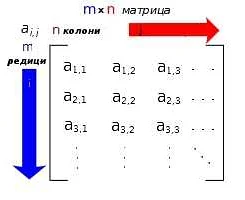
Структура матрицы определяется ее размерностью. Размерность матрицы задается двумя числами: количество строк и количество столбцов. Если матрица содержит n строк и m столбцов, то ее размерность обозначается следующим образом: n x m.
Каждый элемент матрицы обозначается aij, где i — номер строки, а j — номер столбца. Таким образом, матрицу можно представить в виде таблицы:
| a11 | a12 | … | a1m |
| a21 | a22 | … | a2m |
| … | … | … | … |
| an1 | an2 | … | anm |
Количество элементов в строке и столбце матрицы должно быть одинаковым для всех строк и столбцов соответственно. Если строка содержит k элементов, то говорят, что матрица имеет размерность n x k. Аналогично, если столбец содержит l элементов, то говорят, что матрица имеет размерность l x m.
Размерность матрицы
Например, матрица размерности 3 × 2 содержит 3 строки и 2 столбца:
1 2
3 4
5 6
Также существуют матрицы размерности 1 × n (строчные матрицы) и матрицы размерности m × 1 (столбцовые матрицы).
Размерность матрицы важна, так как она определяет, какие операции можно выполнять с этой матрицей. Для сложения и вычитания матрицы должны иметь одинаковую размерность, а для умножения – согласованную размерность.
Операции над матрицами

- Сложение матриц: для сложения двух матриц необходимо сложить соответствующие элементы этих матриц. В результате получится новая матрица той же размерности.
- Вычитание матриц: для вычитания одной матрицы из другой необходимо вычесть соответствующие элементы этих матриц. В результате получится новая матрица той же размерности.
- Умножение матрицы на число: для умножения матрицы на число необходимо умножить каждый ее элемент на это число.
- Умножение матриц: умножение двух матриц определено только в случае, когда количество столбцов у первой матрицы равно количеству строк у второй матрицы. Результатом умножения будет новая матрица, элементы которой вычисляются по определенной формуле.
- Транспонирование матрицы: транспонирование матрицы происходит путем замены строк на столбцы (или столбцов на строки). Таким образом, элемент, находящийся на позиции (i, j) в исходной матрице, будет находиться на позиции (j, i) в транспонированной матрице.
Операции над матрицами обладают определенными свойствами, которые позволяют проводить вычисления и упрощать выражения. Знание основных операций и их свойств является важным для понимания линейной алгебры и решения математических задач.
Транспонирование матрицы
Другими словами, элемент aij из исходной матрицы A становится элементом aji в транспонированной матрице A^T.
Транспонирование матрицы может быть выполнено путем записи элементов строк исходной матрицы в столбцы новой матрицы. Полученная матрица будет отражением исходной матрицы относительно главной диагонали.
Пример транспонирования матрицы:
| 2 | 3 |
| 4 | 5 |
| 6 | 7 |
Транспонированная матрица:
| 2 | 4 | 6 |
| 3 | 5 | 7 |
Транспонирование матрицы имеет ряд свойств:
- Транспонирование транспонированной матрицы даёт исходную матрицу: (A^T)^T = A
- Транспонирование суммы матриц равно сумме транспонированных матриц: (A + B)^T = A^T + B^T
- Транспонирование произведения матриц равно произведению транспонированных матриц в обратном порядке: (AB)^T = B^T * A^T
Транспонирование матрицы используется во многих областях математики и физики. Например, оно может применяться при решении систем линейных уравнений, нахождении обратной матрицы или при работе с векторными пространствами.
Единичная матрица
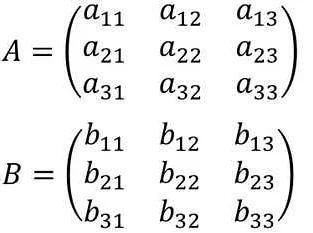
Например, единичная матрица размерности 3×3 выглядит следующим образом:
1 0 0
0 1 0
0 0 1
Единичная матрица является нейтральным элементом при умножении матрицы на другую матрицу. То есть, если матрица A имеет размерность m x n, то выполняется следующее равенство: A * I = I * A = A, где * — операция умножения матрицы.
Единичная матрица также является единственной матрицей, удовлетворяющей этим условиям. Все остальные матрицы с ненулевыми элементами на главной диагонали называются недиагональными матрицами.
Обратная матрица

Обозначается обратная матрица как A-1, где A – исходная матрица.
Для нахождения обратной матрицы A-1 необходимо решить систему линейных уравнений Ax = E, где A – исходная матрица, x – неизвестная матрица, E – единичная матрица.
Обратная матрица имеет ряд свойств:
СвойствоОписание
| Мультипликативное свойство | Если A и B – квадратные матрицы, для которых существует обратная матрица, то (AB)-1 = B-1A-1. |
| Транспонированное свойство | Если A – квадратная матрица, для которой существует обратная матрица, то (A-1)T = (AT)-1. |
| Единичное свойство | Если A – квадратная матрица, для которой существует обратная матрица, то A * A-1 = A-1 * A = E, где E – единичная матрица. |
Обратная матрица является важным инструментом в линейной алгебре и находит применение в различных областях, таких как криптография, статистика, физика и др.
Свойства матриц

- Размерность матрицы. Матрица имеет размерность mxn, где m — количество строк, а n — количество столбцов.
- Элементы матрицы. Каждый элемент матрицы обозначается aij, где i — номер строки, а j — номер столбца.
- Операции над матрицами. Матрицы можно складывать, вычитать и умножать друг на друга.
- Транспонирование. Транспонированная матрица получается путем замены строк на столбцы и столбцов на строки.
- Единичная матрица. Единичная матрица имеет единицы на главной диагонали и нули во всех остальных элементах.
- Обратная матрица. Обратная матрица существует только для квадратной матрицы и обладает свойством, что произведение матрицы на ее обратную даёт единичную матрицу.
- Диагональная матрица. Диагональная матрица имеет нули во всех элементах, кроме главной диагонали.
Эти свойства матриц играют важную роль в линейной алгебре и находят применение в различных областях математики, физики, экономики и других науках.
Вопрос-ответ:
Что такое матрица?
Матрица в математике — это упорядоченный набор чисел, расположенных в виде прямоугольной таблицы. Она состоит из строк и столбцов, которые пересекаются в ячейках.
Какие бывают матрицы?
Матрицы могут быть разных типов, в зависимости от их размерности и содержания. Например, матрицы могут быть квадратными, прямоугольными, нулевыми, единичными и т.д.
Какие свойства имеют матрицы?
Матрицы обладают рядом свойств. Например, они могут складываться и вычитаться, умножаться на число и на другую матрицу, их можно транспонировать и находить определитель. Также матрицы могут быть коммуникативными или ассоциативными при выполнении определенных операций.
Какие применения имеют матрицы в математике?
Матрицы широко применяются в математике и других областях. Например, они используются для решения систем линейных уравнений, анализа и преобразования графов, линейного программирования, криптографии и многих других задач.

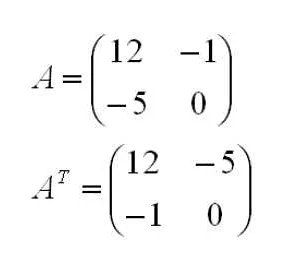


Очень интересная и полезная статья! Я всегда задавалась вопросом, что такое матрица и как она применяется в математике. Теперь благодаря этому материалу я стала гораздо лучше понимать основные определения и свойства матриц. Оказывается, матрица — это таблица, состоящая из чисел, которая используется для решения систем линейных уравнений и других математических задач. Я узнала, что матрицы могут складываться, вычитаться, умножаться на число и друг на друга. Также они могут быть квадратными, прямоугольными и даже пустыми. Это очень важно для решения различных задач в физике, экономике и других науках. Спасибо автору за понятное объяснение и подробные примеры! Теперь я чувствую себя намного увереннее в математике.