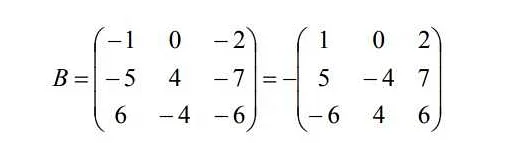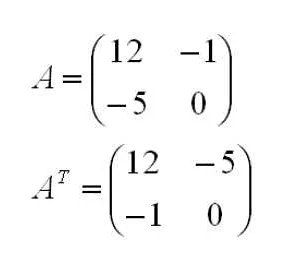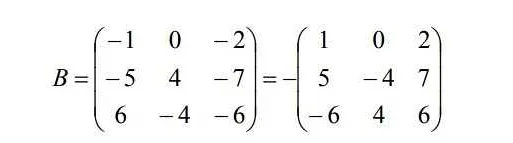Что такое матрица в математике простыми словами как решать

Матрица в математике – это таблица чисел, упорядоченных в строки и столбцы. В данной статье вы узнаете, что такое матрица, как ее решать и какие операции можно выполнять с матрицами.

Матрица – одно из основных понятий в линейной алгебре. Она представляет собой прямоугольную таблицу чисел, упорядоченных в определенный способ. Матрицы широко используются в различных областях математики, физики, экономики, компьютерных наук и других дисциплинах.

Определение матрицы включает в себя указание на количество строк и столбцов, а также элементы, которые находятся в каждой ячейке таблицы. Каждый элемент матрицы имеет свои координаты, обозначаемые номером строки и номером столбца. Например, матрица размером 3×2 содержит 3 строки и 2 столбца. Элементы этой матрицы могут быть числами, символами или другими матрицами.

Простое решение задач, связанных с матрицами, заключается в выполнении операций над ними, таких как сложение, вычитание и умножение. Для сложения и вычитания матриц необходимо, чтобы они были одинакового размера. Умножение матрицы на число выполняется путем умножения каждого элемента матрицы на это число.

Матрицы играют важную роль в линейной алгебре и имеют множество применений в решении различных задач. В дальнейшем изучении математики они становятся неотъемлемой частью и являются основой для более сложных операций и понятий.

Что такое матрица в математике?

Матрица состоит из горизонтальных строк и вертикальных столбцов, при этом размерность матрицы определяется числом строк и столбцов, которые она содержит. Например, матрица размерности 2×3 содержит 2 строки и 3 столбца.

Каждый элемент матрицы обозначается индексом, который состоит из двух чисел: номера строки и номера столбца. Например, элемент матрицы A в строке i и столбце j обозначается как Aij.

Матрицы можно складывать, вычитать и умножать на число. Также можно выполнять операции над матрицами, такие как транспонирование, умножение матрицы на матрицу и умножение матрицы на вектор. Эти операции широко применяются в различных областях математики, физики, экономики и техники.

Матрицы играют важную роль в линейной алгебре и имеют множество приложений в решении реальных задач. Они являются мощным инструментом для описания и анализа систем и процессов.

Видео по теме:

Определение и основные понятия

Матрица может быть представлена как двумерный массив, где каждый элемент обозначается как aij, где i — номер строки, а j — номер столбца.

Размерностью матрицы является количество строк и столбцов. Матрица размерности m x n состоит из m строк и n столбцов.

Матрица может быть квадратной, если количество строк равно количеству столбцов (m = n).

Элементы матрицы могут быть числами, переменными или выражениями.

Матрицы могут быть сложены или вычитаны только если их размерности совпадают.

Умножение матрицы на число выполняется путем умножения каждого элемента матрицы на это число.

Матрицы могут быть умножены только если количество столбцов первой матрицы равно количеству строк второй матрицы.

Транспонирование матрицы — это операция, при которой строки становятся столбцами, а столбцы — строками.

Определитель матрицы может быть вычислен для квадратной матрицы и показывает некоторые свойства матрицы.

Обратная матрица существует только для квадратной матрицы и имеет свои особенности в вычислении.

Простое решение матрицы

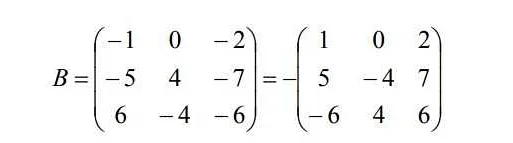
Для решения матрицы можно использовать метод Гаусса. Этот метод позволяет привести матрицу к треугольному виду путем применения элементарных преобразований к строкам. Когда матрица приведена к треугольному виду, можно легко найти решение системы уравнений, представленной матрицей.

Приведение матрицы к треугольному виду выполняется следующим образом:

1. Выбирается главный элемент — элемент с наибольшим по модулю значением в первом столбце матрицы.
2. Строки матрицы переставляются так, чтобы главный элемент был на первом месте.
3. Делится первая строка матрицы на главный элемент, чтобы получить единицу.
4. Из остальных строк вычитается первая строка, умноженная на соответствующий коэффициент, чтобы обнулить элементы под главным элементом.
5. Процесс повторяется для оставшихся столбцов матрицы.

После приведения матрицы к треугольному виду, можно найти решение системы уравнений с помощью обратной подстановки. Начиная с последней строки, выполняется обратная подстановка, позволяющая находить значения переменных поочередно.

Использование метода Гаусса для решения матрицы является достаточно простым и эффективным способом получения решения системы уравнений.

КоэффициентыРезультаты

2	10
3	15

Преобразование матрицы

Преобразование матрицы в математике представляет собой изменение ее элементов по определенным правилам. Существуют различные виды преобразований, которые могут быть применены к матрицам.

Одним из наиболее распространенных преобразований является умножение матрицы на число. При умножении каждого элемента матрицы на заданное число получается новая матрица, в которой все элементы увеличиваются или уменьшаются в заданное количество раз. Например, если умножить матрицу на число 2, то все элементы матрицы будут удвоены.

Другим видом преобразования является сложение или вычитание матриц. При сложении или вычитании соответствующих элементов двух матриц получается новая матрица, в которой элементы являются суммой или разностью элементов исходных матриц. Для выполнения операции сложения или вычитания, матрицы должны иметь одинаковую размерность.

Также существуют преобразования, основанные на элементарных преобразованиях строк или столбцов матрицы. Элементарные преобразования включают в себя перестановку строк или столбцов, умножение строки или столбца на число и сложение строки или столбца с другой строкой или столбцом. Эти преобразования позволяют изменять матрицу таким образом, чтобы получить определенную форму или решить систему уравнений.

Преобразование матрицы является важным инструментом в линейной алгебре и находит применение в различных областях, таких как физика, экономика, компьютерная графика и другие.

Арифметические операции с матрицами

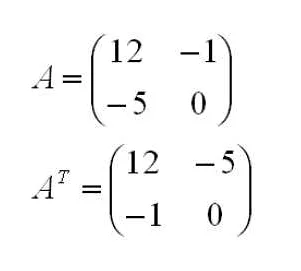
Существуют четыре основных арифметических операции, которые можно выполнять с матрицами:

1) Сложение матриц:

Чтобы сложить две матрицы, необходимо сложить соответствующие элементы матриц попарно. Для этого каждый элемент первой матрицы складывается с соответствующим элементом второй матрицы, и результат записывается в новую матрицу.

2) Вычитание матриц:

Вычитание матриц выполняется аналогично сложению, но вместо сложения элементов происходит их вычитание.

3) Умножение матрицы на число:

Умножение матрицы на число происходит путем умножения каждого элемента матрицы на это число.

4) Умножение матриц:

Умножение матриц является более сложной операцией, которая требует соблюдения определенных правил. Результатом умножения матриц A размером m x n и B размером n x p будет матрица C размером m x p, в которой каждый элемент C[i][j] получается путем умножения элементов i-й строки матрицы A на элементы j-го столбца матрицы B и последующего их сложения.

При выполнении арифметических операций с матрицами важно учитывать их размеры и соответствие. Операции сложения и вычитания возможны только для матриц одинакового размера, а операции умножения матриц можно выполнять только при соблюдении определенных правил размерности.

Арифметические операции с матрицами широко применяются в различных областях, включая физику, экономику, информатику и другие. Они позволяют эффективно решать сложные задачи и моделировать различные процессы.

Применение матриц в решении систем уравнений

Для начала, система уравнений может быть записана в виде матричного уравнения. Коэффициенты уравнений представляются в виде матрицы, а неизвестные переменные — в виде вектора. Затем матричное уравнение может быть решено при помощи операций над матрицами, такими как умножение и сложение, с целью найти значения неизвестных переменных.

Преимущество использования матриц в решении систем уравнений заключается в том, что такой метод позволяет эффективно обрабатывать большие системы уравнений. Матричный подход также обеспечивает удобство и наглядность при выполнении вычислений.

Если система уравнений является совместной, то есть имеет хотя бы одно решение, то решение может быть представлено в виде вектора-столбца. Если система уравнений не имеет решений или имеет бесконечное количество решений, то результатом решения будет соответственно пустое множество или бесконечное множество решений.

Таким образом, использование матриц в решении систем уравнений позволяет нам эффективно находить решения и анализировать различные случаи системы уравнений, что делает этот метод очень полезным в практических приложениях и исследованиях.

Свойства матриц и их классификация

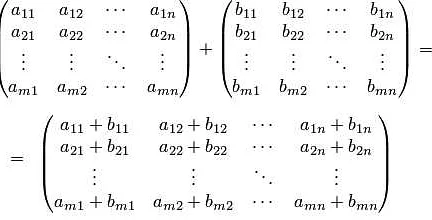
Классификация матриц осуществляется в зависимости от различных свойств и характеристик. Рассмотрим основные классы матриц:

1. Прямоугольная матрица – матрица, у которой количество строк не равно количеству столбцов.
2. Квадратная матрица – матрица, у которой количество строк равно количеству столбцов.
3. Нулевая матрица – матрица, у которой все элементы равны нулю.
4. Единичная матрица – квадратная матрица, у которой все элементы на главной диагонали равны единице, а остальные элементы равны нулю.
5. Симметричная матрица – квадратная матрица, у которой элементы симметричны относительно главной диагонали.
6. Треугольная матрица – квадратная матрица, у которой все элементы ниже (выше) главной диагонали равны нулю.

Классификация матриц позволяет нам лучше понять их особенности и использовать их свойства при решении различных математических задач. Каждый класс матриц имеет свои особенности, отличающие его от других классов.

Применение матриц в физике и экономике

Матрицы играют важную роль в различных областях науки и промышленности, включая физику и экономику. Их применение позволяет решать сложные задачи и моделировать различные процессы.

В физике матрицы используются для описания и анализа физических систем. Они позволяют представить связи между различными величинами, такими как сила, скорость, ускорение и другие физические величины. Например, матрицы могут быть использованы для моделирования движения частиц, электрических цепей или распространения электромагнитных волн. Они также играют важную роль в квантовой механике, где матрицы используются для описания состояний и операторов системы.

В экономике матрицы применяются для анализа и моделирования различных экономических процессов. Например, они могут быть использованы для описания потока товаров и услуг между различными секторами экономики, а также для анализа взаимосвязей между различными экономическими показателями, такими как производство, потребление и инвестиции. Матрицы также используются для оценки экономической эффективности и принятия решений в области финансов и управления ресурсами.

Таким образом, матрицы являются мощным инструментом в физике и экономике, который позволяет анализировать и моделировать сложные системы и процессы. Их применение позволяет улучшить понимание и прогнозирование различных явлений и является неотъемлемой частью современной науки и технологий.

Вопрос-ответ:

Что такое матрица?

Матрица — это упорядоченный прямоугольный массив чисел, элементы которого располагаются в виде таблицы. Количество строк и столбцов определяют размерность матрицы.

Какие операции можно выполнять с матрицами?

С матрицами можно выполнять такие операции, как сложение, вычитание, умножение на число, умножение двух матриц, транспонирование и нахождение определителя и обратной матрицы.

Как решить систему линейных уравнений с помощью матриц?

Для решения системы линейных уравнений с помощью матриц необходимо записать коэффициенты при неизвестных в виде матрицы и вектора свободных членов в виде столбца. Затем решить систему уравнений можно с помощью умножения обратной матрицы на вектор свободных членов.

Какие свойства имеют матрицы?

Матрицы имеют такие свойства, как коммутативность сложения и умножения на число, ассоциативность сложения и умножения на число, дистрибутивность умножения относительно сложения, а также дистрибутивность умножения относительно сложения матриц.

Как найти обратную матрицу?

Обратная матрица для заданной матрицы может быть найдена с помощью формулы, которая зависит от размерности матрицы и ее элементов. Обратная матрица существует только для квадратных матриц, и ее нахождение может быть сложной задачей.

Что такое матрица?

Матрица — это упорядоченная прямоугольная таблица элементов, которая состоит из строк и столбцов.